
- •Литература
- •Перечень компьютерных программ, наглядных и других пособий, методических указаний и материалов и технических средств обучения
- •1.2.Операции над множествами
- •1.3. Булева алгебра множеств
- •1.4. Разбиения и покрытия
- •2. Отношения бинарные и n-арные
- •2.1. Декартово произведение
- •2.2. Бинарные отношения (соответствия)
- •2.3. Операции над бинарными отношениями
- •2.4. Функциональные отношения
- •2.5. Бинарные отношения на множестве
- •2.6. Алгебраические системы
- •3. Основные понятия теории графов
- •3.1. Абстрактный граф
- •3.2. Графическое представление бинарного отношения
- •Множеств а и в
- •3.3. Матричные представления графа
- •3.4. Части графа
- •3.5. Достижимость и связность
- •3.6. Доминирующие множества графа
- •3.7. Независимые множества графа
- •3.8. Раскраска графа
- •3.9.Планарность графов
- •3.10. Инварианты графов
- •4. Булевы функции
- •4.1. Способы задания булевой функции
- •4.2. Элементарные булевы функции и алгебраические формы
- •4.3. Интерпретации булевой алгебры
- •4.4. Нормальные формы булевых функций
- •4.4.1. Дизъюнктивные нормальные формы
- •4.4.2. Конъюнктивные нормальные формы
- •4.5 Полнота и замкнутость системы логических функций
- •4.6. Локальные упрощения днф
- •4.6.1. Удаление избыточных элементарных конъюнкций
- •4.6.2. Удаление избыточных литералов
- •4.7. Графическое представление булева пространства и булевых функций
- •4.7.1. Булев гиперкуб
- •4.7.2. Развертка гиперкуба на плоскости. Карта Карно
- •4.8. Минимизация днф
- •4.8.1. Метод Квайна-МакКласки
- •4.8.2. Метод Блейка-Порецкого
- •4.8.3. Визуально-матричный метод минимизации
- •5. Элементы математической логики
- •5.1 Алгебра высказываний
- •Всякое высказывание логично следует из самого себя.
- •2. Закон противоречия:
- •Если из а следует b, а b ложно, то а тоже ложно.
- •5.2. Логические отношения
- •5.3.Проверка правильности рассуждений
- •5.4. Решение логических задач методом характеристического уравнения
- •5.6. Кванторы
- •5.7 Эквивалентные соотношения. Префиксная нормальная форма
- •6. Основы теории алгоритмов
- •6.1. Интуитивное понятие об алгоритме
- •6.2. Три типа алгоритмических моделей
- •6.3. Кризис теории множеств антиномии. Выводы из антиномий
- •6.4. Машины Тьюринга как модели алгоритмов
- •6.5. Алгоритмы решения некоторых задач теории графов на графах
- •7. Конечный автомат и его описание.
- •7.2. Представления автомата
- •7.3. Связь между моделями Мили и Мура
- •7.4. Автомат с абстрактным состоянием. Булев автомат
- •7.5. Понятие о регулярных выражениях алгебры событий.
- •7.6. Задачи абстрактной теории конечных автоматов
- •8. Комбинаторные задачи и методы комбинаторного поиска
- •8.1. Задачи подсчета числа комбинаторных решений
- •8.2. Особенности оптимизационных комбинаторных задач
- •8.3. Вычислительная сложность
- •8.4. Методы комбинаторного поиска
- •8.5. Задача о кратчайшем покрытии и методы ее решения
- •8.5.1. Постановка задачи
- •8.5.2. Приближенные методы решения задачи
- •8.5.3. Точный метод
- •Вопросы к зачету
- •28. Нормальные формы булевых функций. Дизъюнктивные нормальные формы
- •44. Эквивалентные соотношения. Префиксная нормальная форма
- •Практический раздел Контрольная работа Указания по выбору варианта
- •Контрольное задание №1. Используя диаграммы Эйлера-Венна, решить задачу
- •Методические указания
- •Задачи для самостоятельного решения
- •Контрольное задание №2. Получить сднф, скнф, используя таблицу истинности. Построить днф, кнф, упростив выражение.
- •Методические указания
- •Задачи для самостоятельного решения
- •Контрольное задание №3. Упростить схему (рис. 2)
- •Методические указания
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Методические указания
- •Задачи для самостоятельного решения
- •Контрольное задание №6. Найти инварианты неориентированного графа, заданного матрицей смежности
- •Методические указания
- •Задачи для самостоятельного решения
5. Элементы математической логики
Математическая логика представляет собой формальный математический аппарат, изучающий различные способы логических рассуждений.
Простейшей из формальных логических теорий называют алгебру высказываний. Исчисление высказываний следующая ступень в иерархии формальных теорий. Ещё выше стоят алгебра предикатов и исчисление предикатов.
5.1 Алгебра высказываний
Высказывание – некоторое утверждение, относительно которого нас интересует только его истинность или ложность.
Высказывание называют простым (элементарным), если его истинность не зависит от истинности других высказываний. Высказывание называют сложным (составным), если оно зависит от истинности других высказываний.
В алгебре высказываний объектом исследования является множество высказываний, а операциями – некоторые логические операции, каждую из которых можно рассматривать как некоторое сложное высказывание.
Определяются
эти операции
![]() таблицами истинности. Например, операции
«дизъюнкция» соответствует сложное
высказывание, которое ложно тогда и
только тогда, когдаA
ложно и B
ложно
таблицами истинности. Например, операции
«дизъюнкция» соответствует сложное
высказывание, которое ложно тогда и
только тогда, когдаA
ложно и B
ложно
-
A
B
A\/B
Л
Л
Л
Л
И
И
И
Л
И
И
И
И
В дальнейшем каждое простое высказывание можно связать с некоторой двоичной переменной.

Поэтому сложное высказывание можно связать с некоторой двоичной (логической) функцией.
Используя подобную связь можно сказать, что алгебра высказываний есть одна из интерпретаций алгебры логических функций.
 Запишем
таблицу истинности операций алгебры
высказываний:
Запишем
таблицу истинности операций алгебры
высказываний:
-
A
B
A\/B
A/\B
AB
A↔B
A
 B
B0
0
0
0
1
1
0
0
1
1
0
1
0
1
1
0
1
0
0
0
1
1
1
1
1
1
1
0
Любое сложное высказывание можно представить в виде некоторой формулы. Дадим определение формулы:
Каждый символ a, b, c… есть формула;
Если А и В – формулы, то формулами являются А*В, А\/В, где * - любая операция из других формул нет.
Д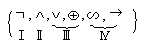 ля
установления порядка выполнения операций
в формулах используются скобки. При их
отсутствии порядок устанавливается
приоритетом операций
ля
установления порядка выполнения операций
в формулах используются скобки. При их
отсутствии порядок устанавливается
приоритетом операций
Вычисление по формуле продемонстрируем на следующем примере:
![]()
-
a
b
c
a
 b
b(a
 b)c
b)c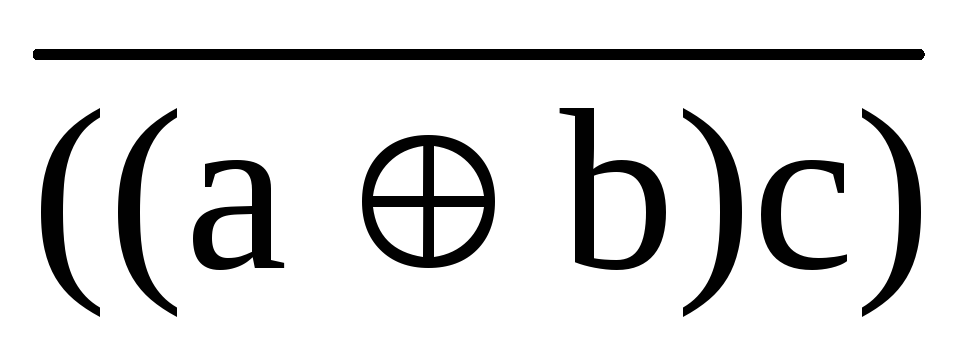

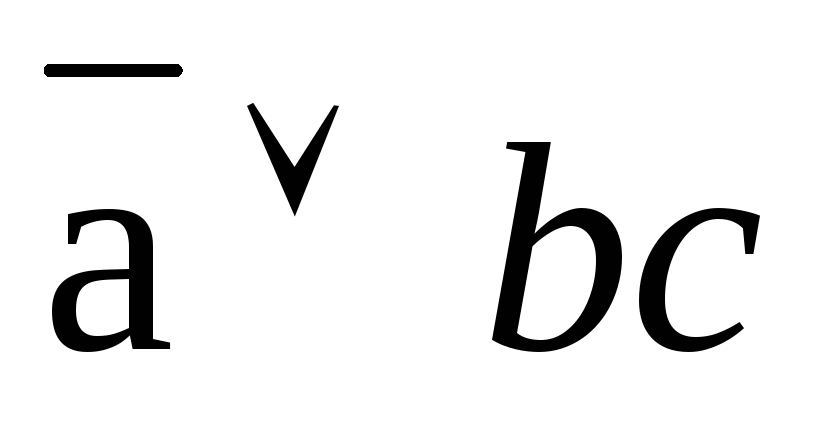
F
0
0
0
0
0
1
1
1
1
0
0
1
0
0
1
1
1
1
0
1
0
1
0
1
1
1
1
0
1
1
1
1
0
1
1
1
1
0
0
1
0
1
0
0
0
1
0
1
1
1
0
0
0
1
1
1
0
0
0
1
0
0
0
1
1
1
0
0
1
0
1
1
В дальнейшем будем говорить, что формула истинна или ложна в зависимости от того, истинно или ложно соответствующее ей высказывание.
Формула может быть истинной при одном наборе значений переменных и ложным при другом наборе. Формула, которая является истинной хотя бы при одном наборе значений переменных, называется выполнимой. Формула ложная при всех наборах значений переменных называется противоречием (тождественно ложной). Формула, истинная при всех наборах значений переменных называется тавтологией (тождественно истинной).
Установить тип формулы можно с помощью таблиц истинности. При большом числе переменных xi (при большом числе простых высказываний) таблицы истинности f(x1,…,xn) функций, соответствующих этим формулам, очень громоздки. Установить тип формулы (выполнима, тавтология, противоречие) удобно с помощью нормальных форм. Для каждой формулы алгебры высказываний можно найти множества КНФ и ДНФ.
Для этого нужно:
Заменить все логические операции булевыми операциями. Это можно сделать, используя следующие равносильные формулы.
А
→С=![]()
![]() C,
А
C,
А
![]() С=А
С=А![]()
![]()
![]() С
С
Заменить знак отрицания относящийся ко всему выражению на знаки относящиеся к отдельным переменным (используя закон де Моргана).
![]() ,
,![]()
Избавиться от знаков двойного отрицания.
 = А
= АПрименить, если нужно, закон дистрибутивности и формулы поглощения. A
 AВ
= A, A(AС)
= A
AВ
= A, A(AС)
= A
Пример:
Пусть
S = (А →С)↔(
![]() →
→![]() ).
Построим
КНФ для этой формулы.
).
Построим
КНФ для этой формулы.
1)
Избавимся от знаков импликации, получим
(![]()
![]() C)↔(
C)↔(![]()
![]()
![]() ).
).
2)
Учитывая, что
![]() = А , имеем: S = (
= А , имеем: S = (![]()
![]() С)↔(A
С)↔(A![]()
![]() )
.
)
.
3) Избавимся от знака двойной импликации:
S
= ((![]()
![]() (A
(A![]()
![]() ))
))![]() ((
((![]()
![]() C)
C)![]()
![]() ).
).
4)
Применим закон де Моргана:
![]() =
=
![]()
![]() ;
;
![]() =
=![]()
![]() .
.
Получим
S =(![]() C
C![]() (A
(A![]()
![]() ))
))![]() ((
((![]()
![]() C)
C)
![]()
![]()
![]() ).
).
5)
Избавимся от двойных отрицаний
![]() = А,
= А,
![]() = В в формуле S.
Учитывая закон ассоциативности операции
дизъюнкции внутренние
скобки опустим:
= В в формуле S.
Учитывая закон ассоциативности операции
дизъюнкции внутренние
скобки опустим:
S
= (A![]()
![]() A
A![]()
![]() )
)![]() (
(![]()
![]() C
C![]()
![]() B).
B).
6)
Применим
формулу
поглощения:
A![]() A
A![]() = A;
= A;
![]()
![]()
![]() B
=
B
=![]() Получим
S = (A
Получим
S = (A![]()
![]() )
)![]() (
(![]()
![]() C).
C).
Получили КНФ для исходной формулы.
Теорема 1: формула алгебры высказываний является тождественно истинной, когда каждый множитель её КНФ содержит пару слагаемых, одно из которых является элементарным высказыванием, а другое его отрицанием.
Теорема 2: формула алгебры высказываний является тождественно ложной, когда каждый множитель её ДНФ содержит пару сомножителей, один из которых является элементарным высказыванием, а другое его отрицанием.
Между формулами можно установить отношение формально импликации (=>). Формулы А и В находятся в отношении формальной импликации, точнее А имплицируем В (А=>В), если формула В истинна на всех наборах переменных, на которых истинна формула А. В таких случаях говорим, что формула В логически следует из формулы А.
Формулы А и В равносильны (логически эквивалентны) (А<=>В) если любая из них следует из другой. Очевидно, что таблица истинности равносильных формул совпадают.
Рассмотрим основные тавтологии использования высказываний.
1.Закон
тождествия:
![]()
