
- •Міністерство освіти і науки України
- •Ббк 22.1я73
- •Правила оформлення контрольної роботи:
- •Основні питання програми
- •Модуль 1 Системи рівнянь, вектори та аналітична геометрія
- •1.1. Визначники, матриці, розв’язання систем лінійних рівнянь
- •1.2. Елементи векторної алгебри
- •1.3. Пряма на площині
- •1.4. Криві другого порядку
- •1.5. Площина та пряма в просторі
- •Модуль 2 вступ в математичний аналіз
- •2.1. Розкриття невизначеностей, і і іі визначні границі
- •2.2. Диференціальне числення функцій однієї змінної
- •Основні правила диференціювання:
- •2.3. Застосування похідних для дослідження функцій
- •2.4. Похідні в механіці
- •2.5. Диференціальне числення функцій декількох змінних
- •Модуль 3 нЕвизначений і визначений інтеграли
- •3.1. Основні методи інтегрування
- •Основні властивості невизначеного та визначеного інтегралів:
- •3.2. Невласні інтеграли
- •3.3. Застосування визначених інтегралів
- •Модуль 4 диференціальні рівняння
- •4.1. Розв’язання диференціальних рівнянь деяких типів
- •Модуль 5 кратні, криволінійні та поверхневі інтеграли
- •5.1. Подвійні, потрійні інтеграли та їх застосування
- •5.2. Криволінійні інтеграли
- •Модуль 6 числові і степеневі ряди
- •6.1. Числові ряди
- •Ознака Даламбера. Якщо для знакододатного ряду існує
- •6.2. Степеневі ряди
- •Модуль 7 комплексні числа. Елементи теорії функцій комплексної змінної
- •7.1. Комплексні числа
- •7.2. Обчислення значень елементарних функцій
- •Модуль 8. Теорія ймовірностей і елементи математичної статистики
- •8.1. Основні поняття і теореми теорії ймовірностей
- •8.2. Дискретні випадкові величини
- •8.3. Неперервні випадкові величини
- •8.4. Біноміальний та пуассонів закони розподілу
- •8.5. Нормальний, рівномірний та показниковий закони
- •Числові характеристики: , . (8.5.7)
- •8.6. Елементи математичної статистики
- •Контрольна робота № 1 Модуль 1. Системи рівнянь, вектори та аналітична геометрія
- •Модуль 2. Вступ в математичний аналіз
- •Модуль 3. Невизначений і визначений інтеграли
- •Модуль 4. Диференціальні рівняння
- •Контрольна робота № 2 Модуль 5. Кратні, криволінійні та поверхневі інтеграли
- •Модуль 6. Числові і степеневі ряди
- •Література
- •Таблиця значень функції Гаусса
- •Продовження додатка а Таблиця значень функції Гаусса
- •Додаток б Таблиця значень функції Лапласа
- •Продовження додатка б Таблиця значень функції Лапласа
- •Додаток в Значення (розподіл Пуассона)
- •Продовження додатка в Значення (розподіл Пуассона)
2.2. Диференціальне числення функцій однієї змінної
Диференціювання функцій є найбільш ефективним методом їх дослідження. Вихідним моментом в оволодінні технікою диференціювання є засвоєння таблиці похідних основних елементарних функцій:
|
1) |
5) |
9) |
|
2) |
6) |
10) |
|
3) |
7) |
11) |
|
4) ,
|
8) |
12) |
Основні правила диференціювання:
, (2.2.1)
, (2.2.2)
, (2.2.3)
, (2.2.4)
, (2.2.5)
![]() ,
або
,
або
![]() ,
(2.2.6)
,
(2.2.6)
тобто похідна складної функції (або , ) дорівнює добутку похідної функції по проміжному аргументу на похідну проміжного аргументу по кінцевому аргументу х.
Диференціалом
функції
![]() називається добуток похідної на
диференціал змінної:
називається добуток похідної на
диференціал змінної:
![]() .
(2.2.7)
.
(2.2.7)
Приклад
2.2.1. Знайти
похідну функцій:
![]() ,
,![]() .
.
Розв’язання.
Похідна
складної функції
![]() і, якщо
і, якщо
![]() ,
то
,
то
![]()
![]() .
.
Функція
![]() також є складною, тому згідно (2.2.6) маємо:
також є складною, тому згідно (2.2.6) маємо:
![]()
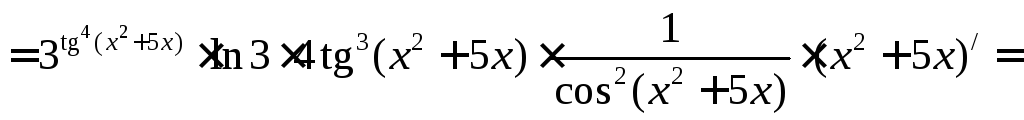
 ,
або записуємо відразу:
,
або записуємо відразу:
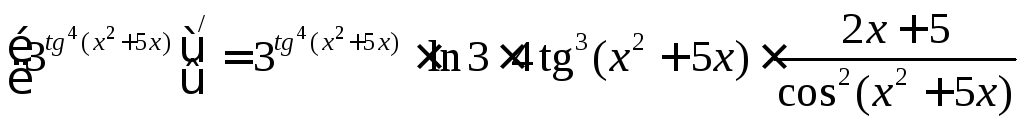 .
.
Похідна
неявної функції. Якщо
функція
![]() задана рівнянням
задана рівнянням![]() ,
то для знаходження похідної
,
то для знаходження похідної![]() потрібно продиференціювати обидві
частини цього рівняння, розглядаючи
потрібно продиференціювати обидві
частини цього рівняння, розглядаючи![]() як функцію від
як функцію від![]() ,
а потім отримане рівняння розв'язати
відносно
,
а потім отримане рівняння розв'язати
відносно![]() .
.
Інколи
доцільно перед диференціюванням функції
спочатку логарифмувати, а потім знайти
похідну отриманої неявної функції.
Такий спосіб називається логарифмічним
диференціюванням. Завдяки йому значно
спрощується знаходження похідних
показниково-степеневих функцій
![]() .
.
Диференціювання
функцій, заданих параметрично, тобто
функцій виду
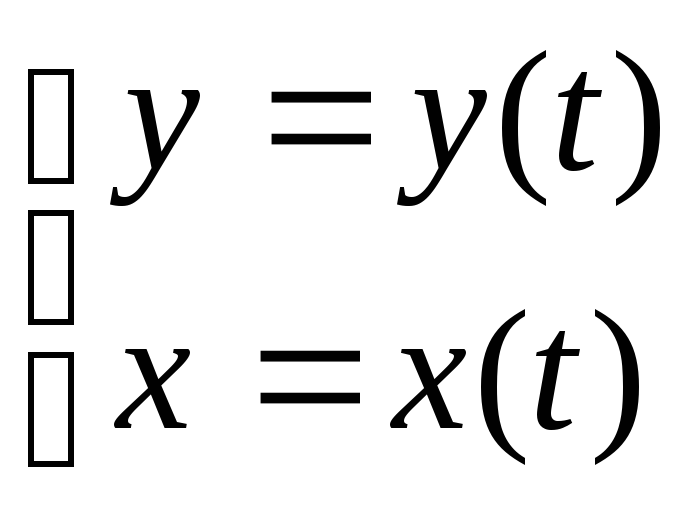 , здійснюється за формулою
, здійснюється за формулою
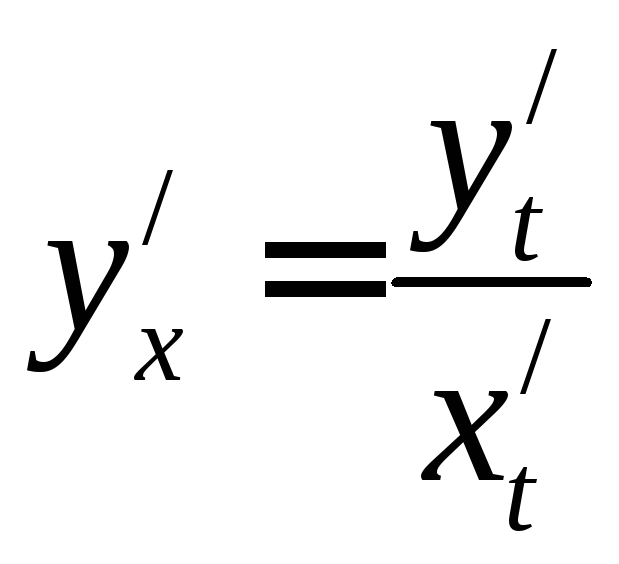 .
(2.2.8)
.
(2.2.8)
Приклад
2.2.2. Знайти
похідну
![]() функції
функції
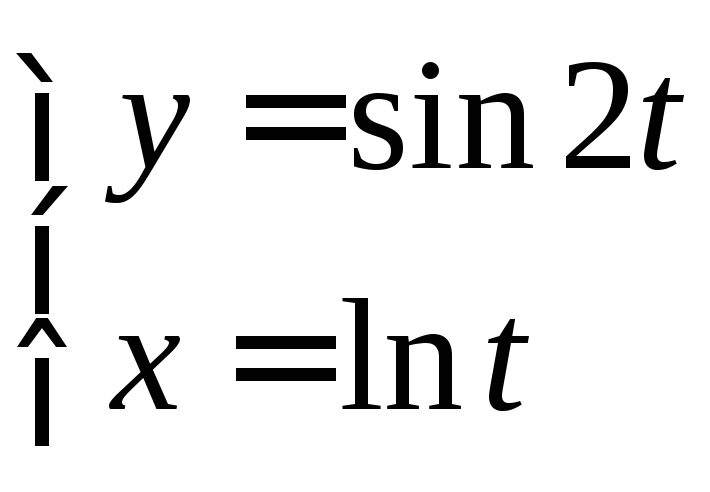 .
.
Розв’язання.
Похідну
параметрично заданої функції знайдемо
за формулою (2.2.8):
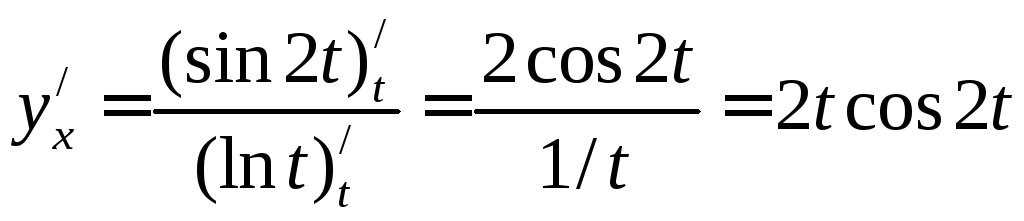 .
.
Приклад
2.2.3. Знайти
похідну
![]() функції
функції![]() .
.
Розв’язання.
Щоб знайти похідну
![]() неявної функції, продиференціюємо
спочатку обидві частини цього рівняння,
розглядаючи
неявної функції, продиференціюємо
спочатку обидві частини цього рівняння,
розглядаючи
![]() як
функцію від
як
функцію від
![]() :
:
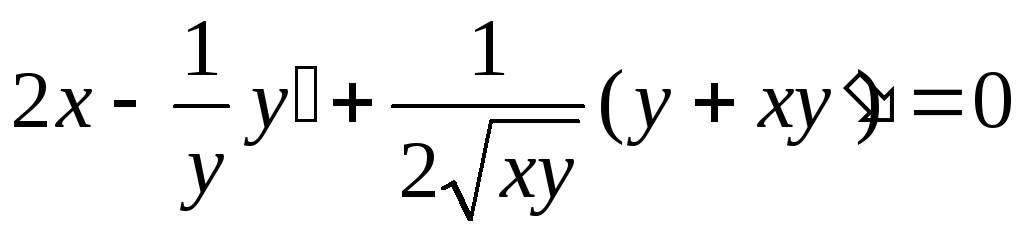 .
Тоді
.
Тоді .
Звідси знайдемо
.
Звідси знайдемо
![]() :
:
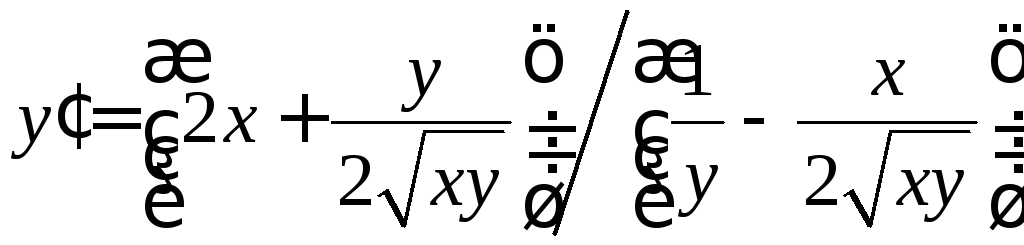 ,
або (якщо помножити чисельник і знаменник
на
,
або (якщо помножити чисельник і знаменник
на![]() )
)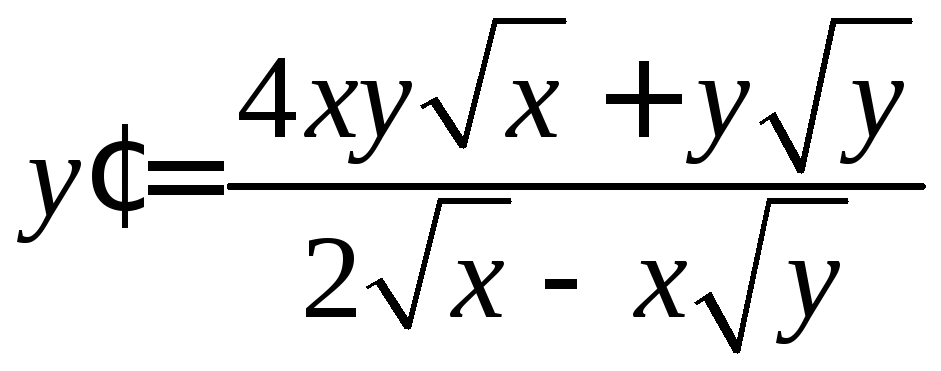 .
.
Приклад
2.2.4. Знайти
похідну функції
![]() .
.
Розв’язання.
Спочатку
логарифмуємо:
![]() ,
тобто
,
тобто![]() .
.
Диференціюємо
по
![]() ліву і праву частини одержаної рівності
(враховуємо, що справа – добуток функцій):
ліву і праву частини одержаної рівності
(враховуємо, що справа – добуток функцій):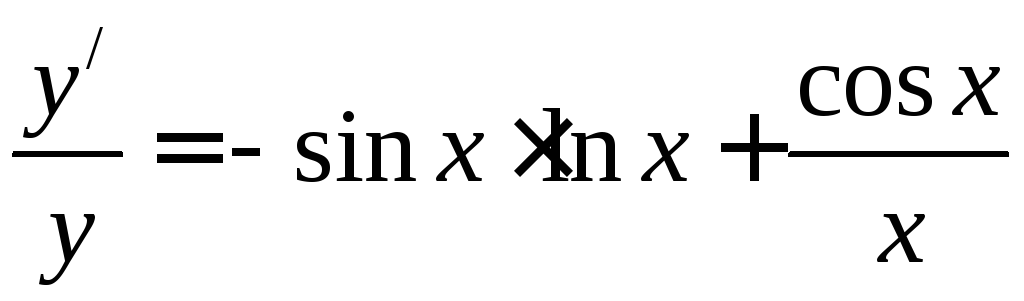 ,
звідки
,
звідки ,
або
,
або ,
тому що
,
тому що![]() .
.
Зауважимо, що приклади 2.2.1, 2.2.3, 2.2.4 відповідають завданню 2.2 контрольної роботи.
Література: [1, с. 147 ‑ 169], [2, с. 160 ‑ 182], [3, с. 305 – 339], [8].
2.3. Застосування похідних для дослідження функцій
Дослідження функцій методами диференціального числення можна проводити у відповідності з такою схемою:
Знаходження області визначення функції і точок розриву.
Визначення парності або непарності функції, її періодичності.
Визначення точок перетину графіком функції осей координат та інтервалів знакосталості функції.
Уточнення поведінки функції в околах точок розриву, та при
 .
Знаходження асимптот графіка функції.
.
Знаходження асимптот графіка функції.Визначення інтервалів монотонності, екстремумів функції.
Визначення інтервалів опуклості та угнутості, точок перегину.
Побудова графіка функції.
Зупинимося на деяких пунктах дослідження докладніше.
Пряма
називається
асимптотою графіка функції
, якщо відстань від точки
![]() на графіці до цієї прямої прямує до нуля
при віддаленні точки
на графіці до цієї прямої прямує до нуля
при віддаленні точки![]() уздовж кривої в нескінченність.
Розрізняють три види асимптот: вертикальні,
горизонтальні, похилі. Якщо , то
уздовж кривої в нескінченність.
Розрізняють три види асимптот: вертикальні,
горизонтальні, похилі. Якщо , то![]() ‑вертикальна
асимптота
(функція має розрив при
‑вертикальна
асимптота
(функція має розрив при
![]() ).
Якщо (або ), то пряма (або ) є
горизонтальною асимптотою.
Похила
асимптота
має вигляд , де
).
Якщо (або ), то пряма (або ) є
горизонтальною асимптотою.
Похила
асимптота
має вигляд , де
, , (2.3.1)
якщо зазначені границі існують.
Точки області визначення функції, в яких похідна дорівнює нулеві або не існує, називаються стаціонарними (критичними). Інтервал, на якому похідна від’ємна, є інтервалом спадання; інтервал, на якому похідна додатна, є інтервалом зростання. Знайдені стаціонарні точки потрібно нанести на числову пряму і встановити знак першої похідної зліва і справа від стаціонарної точки. Так визначають проміжки монотонності і наявність екстремуму функції. Екстремуми мають місце лише в тих критичних точках, де виконується достатня умова існування екстремума: якщо при переході через стаціонарну точку похідна змінює свій знак, то в стаціонарній точці є екстремум. Це максимум, якщо знак змінюється з плюса на мінус, і мінімум, якщо знак змінюється з мінуса на плюс.
Якщо друга похідна (тобто похідна від першої похідної) на інтервалі додатна, то графік функції угнутий, якщо друга похідна – від’ємна, то графік функції опуклий. Точки (де функція визначена), що розділяють інтервали опуклості й угнутості, називаються точками перегину. Друга похідна (якщо вона існує) в точці перегину дорівнює нулю.
Приклад
2.3.1.
Знайти
інтервали
монотонності та екстремуми функції
![]() ,
а також інтервали опуклості і точки
перегину.
,
а також інтервали опуклості і точки
перегину.
Розв’язання.
Маємо
![]() .
Стаціонарна точка:
.
Стаціонарна точка:
![]() .
Щоб знайти інтервали, де
.
Щоб знайти інтервали, де
![]() (або
(або
![]() )
скористаємось методом інтервалів
розв’язання
нерівностей. Для цього нанесемо на вісь
стаціонарні точки і (наприклад, за
допомогою підстановки у
)
скористаємось методом інтервалів
розв’язання
нерівностей. Для цього нанесемо на вісь
стаціонарні точки і (наприклад, за
допомогою підстановки у
![]() контрольних точок) з’ясуємо знак
похідної на кожному інтервалі:
контрольних точок) з’ясуємо знак
похідної на кожному інтервалі:
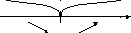
![]()
– +
![]() 2
2![]()
Рис. 2.3.1 – Знаки похідної за методом інтервалів
При
![]() (контрольна точка
(контрольна точка![]() ,
,
![]() )
)
![]() ,
а при
,
а при![]() (контрольна точка
(контрольна точка![]() ,
,
![]() )
)
![]() .
Отже, функція
.
Отже, функція
![]() спадає на интервалі
спадає на интервалі
![]() та зростає на интервалі
та зростає на интервалі![]() .
.
При
переході через точку
![]() знак похідної змінюється з“
- ” на
“ + ”, отже
знак похідної змінюється з“
- ” на
“ + ”, отже
![]() ‑ точка мінімуму. При цьому
‑ точка мінімуму. При цьому
![]() .
.
Знайдемо
інтервали опуклості графіка функції:
![]() ,
отже фунція є угнутою при
,
отже фунція є угнутою при![]() і не має точок перегину.
і не має точок перегину.
Приклад
2.3.2.
Засобами
диференціального числення дослідити
функцію
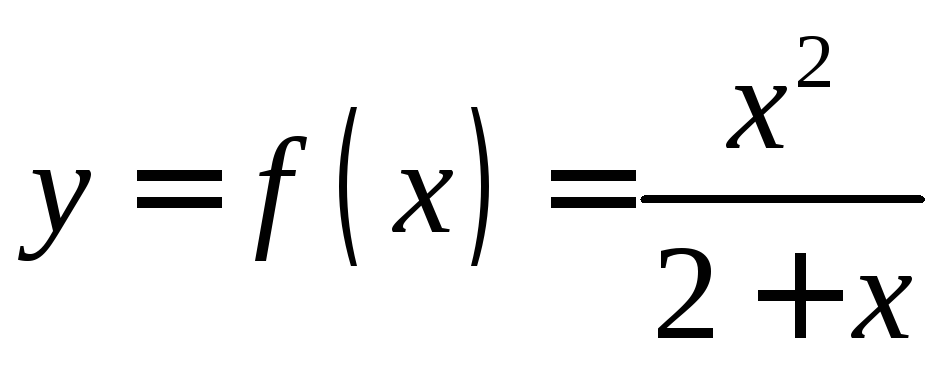 та побудувати її графік.
та побудувати її графік.
Розв’язання.
1. Область
визначення функції:
![]() .
.
![]() – точка розриву функції.
– точка розриву функції.
2. Функція
– не парна (бо
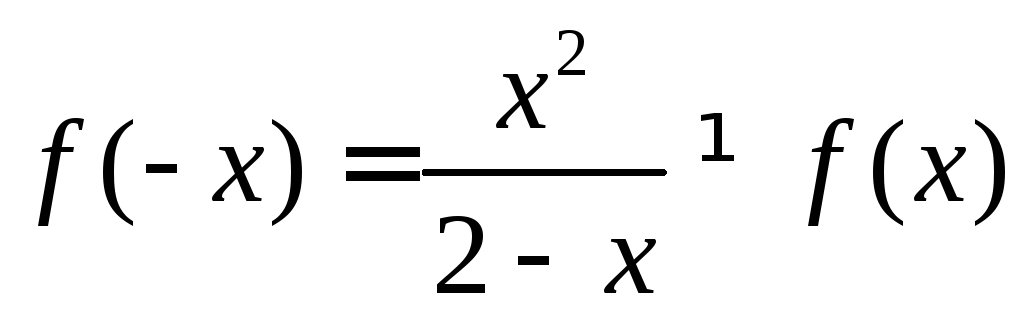 ) і не непарна (бо
) і не непарна (бо![]() ). Функція – не періодична.
). Функція – не періодична.
3. Функція
перетинає осі координат в точці
![]() .
.
![]() при
при
![]() ,
і
,
і
![]() при
при
![]() .
.
4. Оскільки
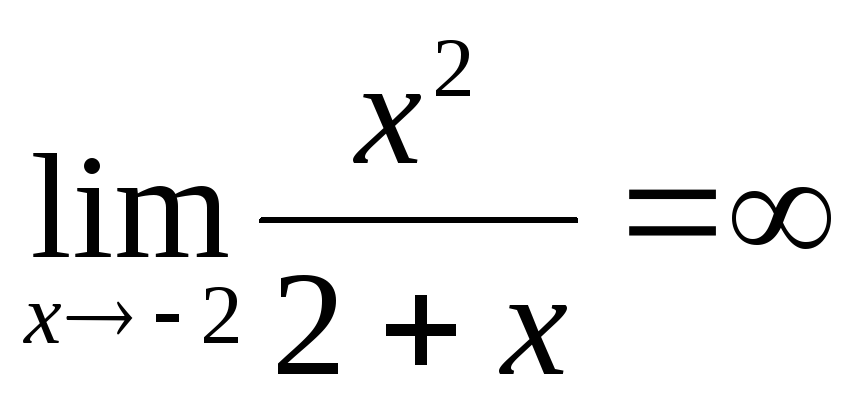 ,
то
,
то
![]() – вертикальна асимптота. Оскільки
– вертикальна асимптота. Оскільки
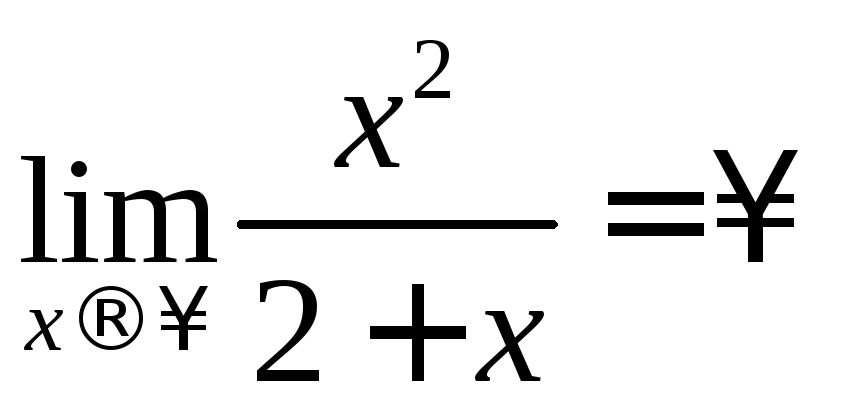 ,
то горизонтальної асимптоти немає.Знайдемо
похилі асимптоти графіка функції:
,
то горизонтальної асимптоти немає.Знайдемо
похилі асимптоти графіка функції:
![]() ;
;
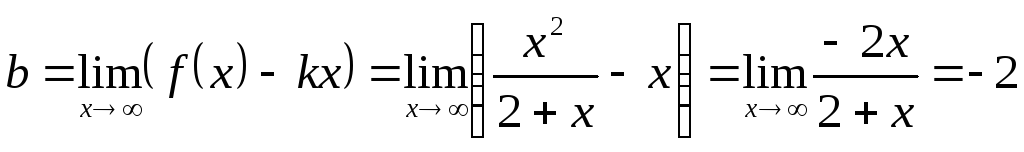 ,
таким чином,
,
таким чином,
![]() – похила асимптота.
– похила асимптота.
5. Знайдемо проміжки зростання, спадання і точки екстремуму.
Похідна (за (2.2.5)):

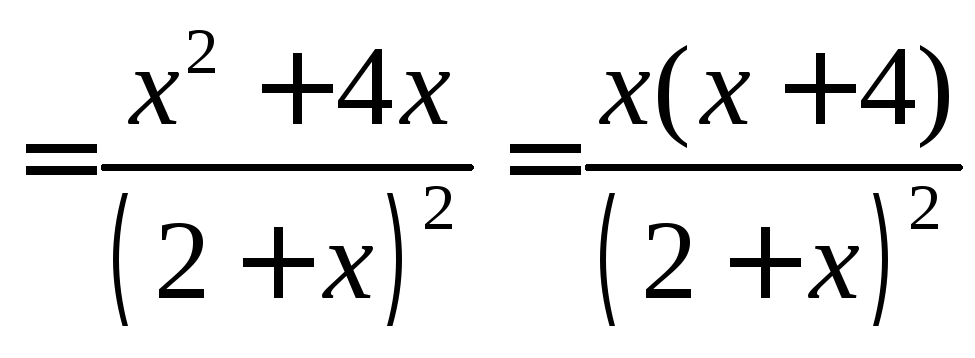 .
.
В
точці
![]() похідна функції не існує, а в точках
похідна функції не існує, а в точках![]() і
і
![]() похідна
похідна
![]() .Точки
.Точки
![]() розбивають область визначення функції
на інтервали
розбивають область визначення функції
на інтервали![]() ,
,![]() ,
,![]() і
і![]() .
.
![]() при
при
![]() ,
значить функція зростає на цих інтервалах.
,
значить функція зростає на цих інтервалах.
![]() на
інтервалах
на
інтервалах
![]() і
і
![]() ,
значить функція спадає на цих інтервалах.
,
значить функція спадає на цих інтервалах.
![]() –точка
максимуму і
–точка
максимуму і
![]() .
.
![]() –точка
мінімуму і
–точка
мінімуму і
![]() .
.
6. Знайдемо проміжки опуклості, угнутості і точки перегину.
Друга
похідна:
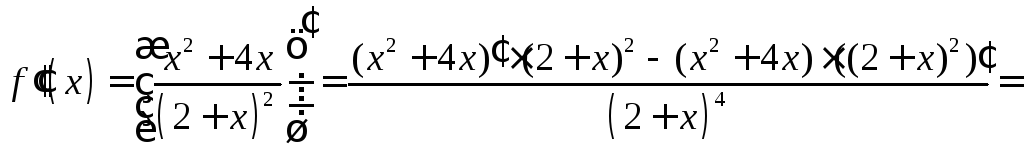
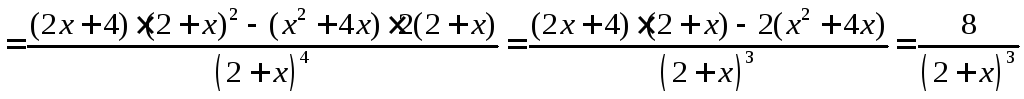 .
.
![]() в
усіх точках з області визначення функції.
Точка розриву функції розбиває область
визначення на два інтервали
в
усіх точках з області визначення функції.
Точка розриву функції розбиває область
визначення на два інтервали
![]() і
і
![]() .
.
Якщо
![]() ,
то
,
то
![]() – графік функції є опуклим.
– графік функції є опуклим.
Якщо
![]() ,
то
,
то![]() – графік функції є угнутим.
– графік функції є угнутим.
Точок перегину немає.
Всі дані заносимо в таблицю 2.3.1.
Таблиця
2.3.1 – Дослідження функції

|
|
|
|
|
|
|
|
|
|
|
+ |
0 |
– |
не існує |
– |
0 |
+ |
|
|
– |
– |
– |
не існує |
+ |
+ |
+ |
|
|
< 0
|
= ‑ 8 max |
< 0
|
не існує |
> 0
|
= 0 min |
> 0
|
7. Побудуємо графік функції:
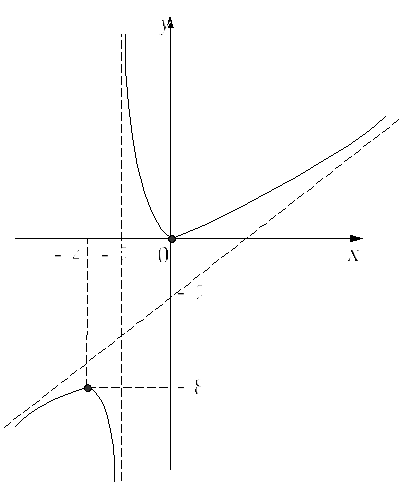
Рис.
2.3.2 – Графік функції

Зауважимо, що приклад 2.3.2 відповідає завданню 2.3 контрольної роботи.
Література: [1, с. 170 ‑ 196], [2, с. 191 ‑ 216], [3, с. 401 – 416], [9].
