1.2. Елементи векторної алгебри

Щоб знайти координати вектора , потрібно із координат його кінця відняти координати початку :

. (1.2.1)

Довжина (модуль) вектора дорівнює кореню квадратному із суми квадратів його координат:

. (1.2.2)

Ортом або одиничним вектором називається вектор, довжина якого дорівнює одиниці. Координатні орти:

.

При складанні (відніманні) векторів їхні координати складаються (віднімаються), а при множенні вектора на число його координати помножуються на це число.

Скалярним добутком векторів іназивається число, що дорівнює добутку їхніх довжин на косинус кута між ними:

. (1.2.3)

Якщо ,тодіскалярний добуток

. (1.2.4)

Якщо матеріальна точка (тіло) під дією постійної за величиною і напрямом сили переміщується уздовж вектора, торобота сили обчислюється за формулою :

. (1.2.5)

Векторний добуток – це вектор

. (1.2.6)

Якщо вектори імають спільний початок, то модуль векторного добутку дорівнює площі паралелограма, побудованого на цих векторах (обо подвоєній площі прямокутника).

Мішаним добутком трьох векторів,іназивається їх векторно-скалярний добуток:

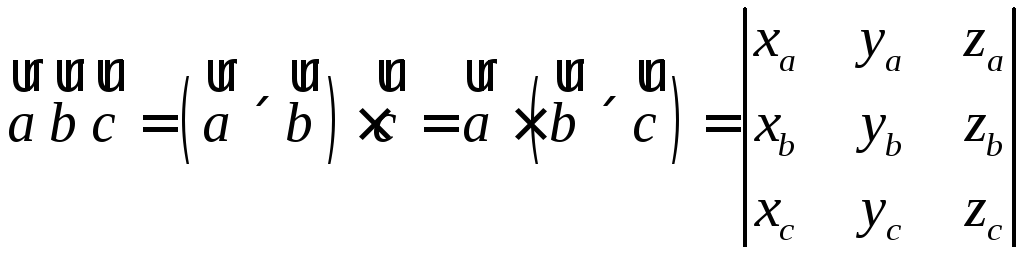. (1.2.7)

Якщо вектори ,імають спільний початок, то модуль мішаного добутку дорівнюєоб’ємові паралелепіпеда, побудованого на цих векторах (обо шести об’ємам піраміди).

У випадку

, (1.2.8)

то вектори ,ієкомпланарними, тобто лежать в одній площині.

Вектори ,єколінеарними (), якщо

, (1.2.9)

де ‑ ненульове число.

Вектори ,єортогональними (), якщо

. (1.2.10)

Приклад 1.2.1. За координатами вершин , , , піраміди знайти: а) довжину сторони , б) косинус кута між ребрами і, в) об’єм піраміди , г) роботу рівнодіючої сил і , під дією якої тіло переміщується прямолінійно з точки в точку .

Розв’язання. Знайдемо вектори ,,за формулою (1.2.1):, , .

а)  Тоді за формулою (1.2.2) довжина сторони дорівнює (од.)

б)  Згідно (1.2.3) та (1.2.4):

.

в)  Об’єм піраміди (шоста частина об’єма паралелепіпеда, побудованого на тих самих векторах) із застосуванням (1.2.7):

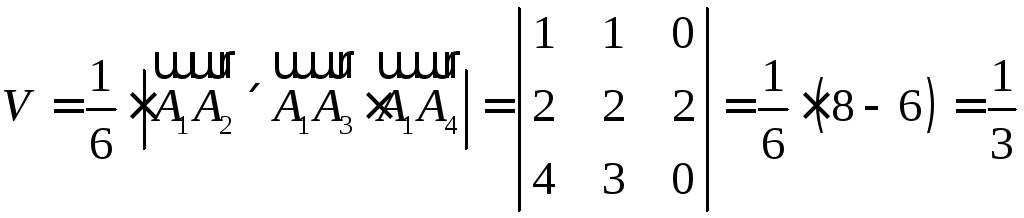(куб. од.),

г)  Рівнодіюча сил і ‑ це сила, робота цієї сили згідно (1.2.5):

.

Зауважимо, що приклад  1.2.1 відповідає завданню  1.2 контрольної роботи.

Література: [1, с. 296 ‑ 315], [2, с. 402 ‑ 432], [3, с. 12 – 22, 35 ‑ 63], [5], [6].

1.3. Пряма на площині

Загальне рівняння прямої:

. (1.3.1)

(‑ сталі числа,і одночасно нулю не дорівнюють).

Рівняння прямої, яка має кутовий коефіцієнт k (тангенс кута між прямою і додатною піввіссю Ох) і перетинає вісь Оу в точці, ордината якої дорівнює b, має вид:

. (1.3.2)

Рівняння прямої, яка проходить через точку в заданому напрямку:

. (1.3.3)

Рівняння прямої, що проходить через дві задані точки і, має вигляд:

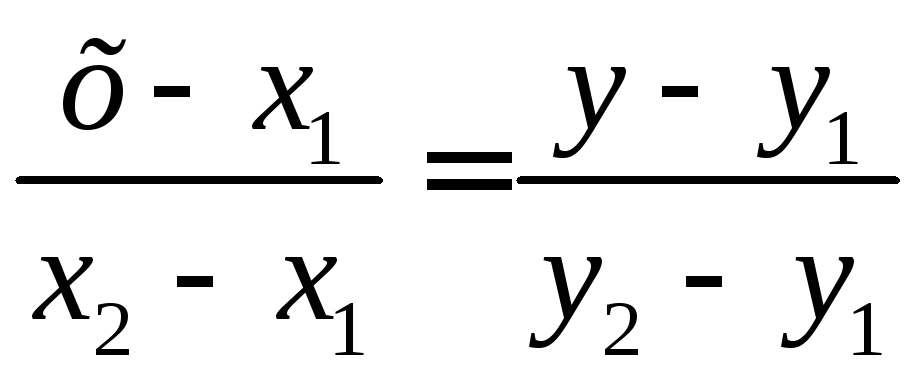. (1.3.4)

Рівняння прямої “у відрізках” на осях координат

. (1.3.5)

є зручним для побудови прямої на площині (пряма проходить через точки і, що розташовані на осях Ох і Оу відповідно).

Рівняння прямої, паралельної осі Ох, записується у вигляді , а прямої, паралельної осіОу ‑ у виді .

Якщо є дві прямі (або ),, то

тангенс кута між прямими і:

. (1.3.6)

(знак плюс відповідає гострому куту , а знак мінус – тупому).

Умова паралельності прямих ():

, або 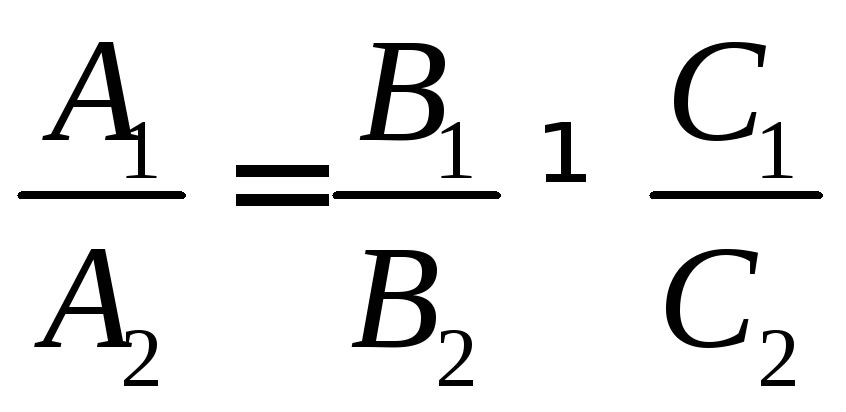. (1.3.7)

Умова перпендикулярності ():

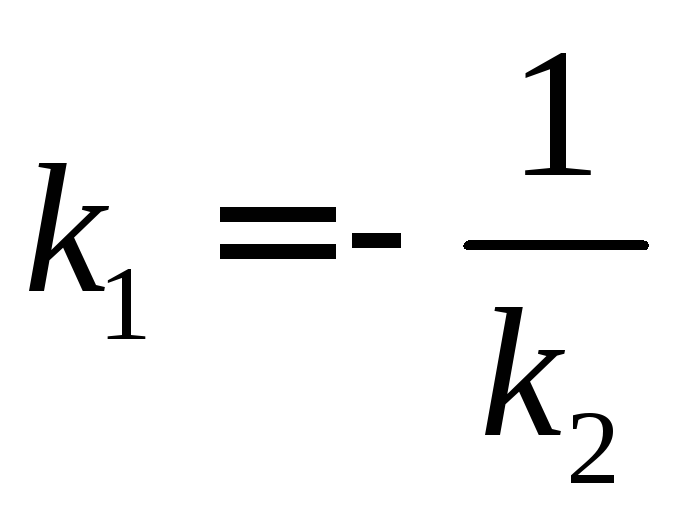, або . (1.3.8)

Відстань точки до прямої знаходиться за формулою

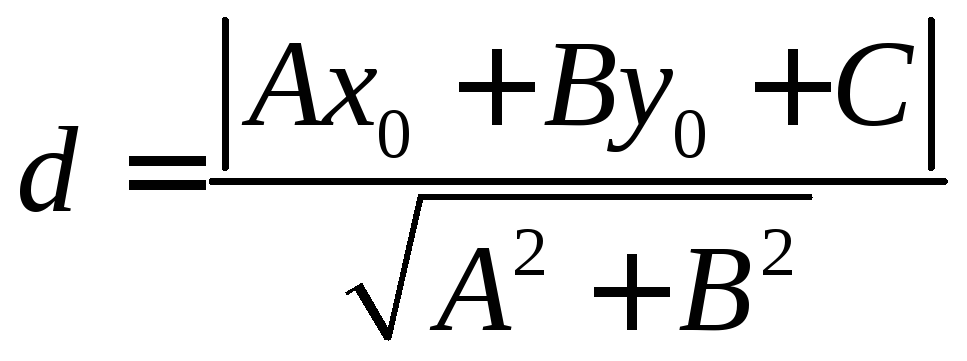. (1.3.9)

Приклад  1.3.1. За координатами вершин ,,трикутника знайти: а) рівняння лінії , б) рівняння висоти , в) довжину висоти.

Розв’язання. а) Знайдемо рівняння лінії, що проходить через точки і : , або, тобто. Таким чином, загальне рівняння : .

б) Запишемо спочатку рівняння з кутовим коефіцієнтом: . Таким чином,‑кутовий коефіцієнт прямої . Пряма , значить кутовий коефіцієнт прямої згідно (1.3.8) дорівнює . Користуючись рівнянням прямої (1.3.3), яка проходить через точку в заданому напрямку, маємо рівняння : , або ,,.

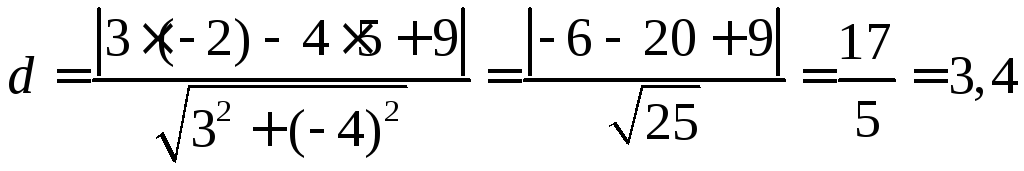в) Довжина висоти ‑ це відстань точки до прямої . Значить, за формулою (1.3.9)  (од.)

Зауважимо, що приклад  1.3.1 відповідає завданню  1.3 контрольної роботи.

Література: [1, с. 15 ‑ 45], [2, с. 33 ‑ 53], [3, с. 123 – 127], [5], [6].