7.2. Обчислення значень елементарних функцій

комплексної змінної

Основні елементарні функції комплексної змінної визначаються наступними формулами:

Показникова функція:

. (7.2.1)

Тригонометричні функції:

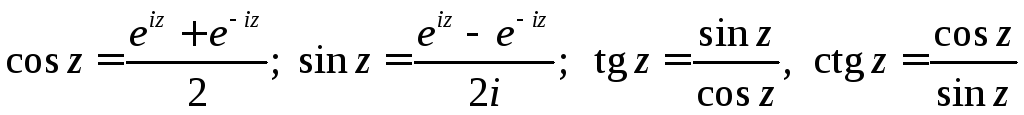. (7.2.2)

Логарифмічна функція (для ):

, (). (7.2.3)

Головне значення логарифма ():

. (7.2.4)

Узагальнені показникова і степенева функції:

(). (7.2.5)

Приклад 7.2.1. Обчислити значення: 1)  , 2), 3)  , 4).

Розв’язання. 1)  Згідно (7.2.1) маємо:

.

2) За формулою (7.2.2):

.

3)  Згідно (7.2.3) маємо (при ):

4)  За формулою (7.2.5): , де.

Приклад 7.2.2. За даними комплексними числами та знайти: а)  модуль та аргумент числа та записатиу тригонометричній та показниковій формах, б), в)  всі значеннята зобразити їх на комплексній площині, г),д),,.

Розв’язання. а) Якщо , то,. Тоді модуль за (7.1.2):, головне значення аргумента (згідно схеми 7.1.1):, аргумент(). Значить,‑ тригонометрична форма,‑показникова форма числа .

б) Користуючись тригонометричною формою числа та формулою Муавра(7.1.9) маємо:

.

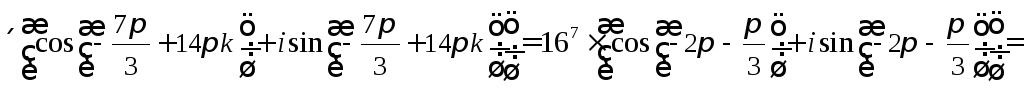
Таким чином, 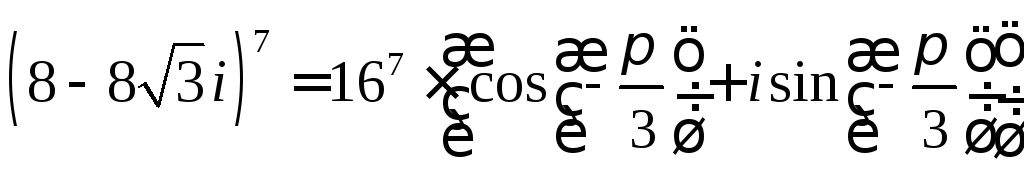‑тригонометрична форма, 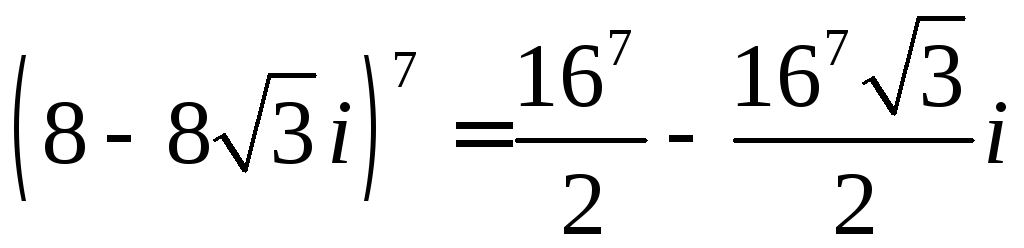‑ алгебраїчна форма числа .

в) Користуючись тригонометричною формою числа маємо: де .Випишемо чотири різних значення кореня (в тригонометричній формі), беручі по черзі :

.

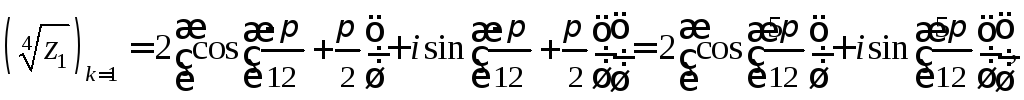
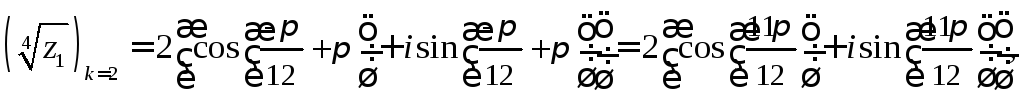
Для геометричного представлення знайдених значень кореня можна зобразити одне значення, наприклад ‑ це точка кола радіусу , що лежить на промені . Після цього будуємо квадрат, вписаний у коло. Вершини цього квадрата будуть являти собою чотири значення .

г) Значення логарифмічної функції (в алгебраїчній формі): (), головне значення логарифма:.

д) , тобто,. Значить, значення показникової функції,(для дійсного числа спряжене співпадає з самим числом). Тоді значення тригонометричних функцій (валгебраїчній формі): ,,.

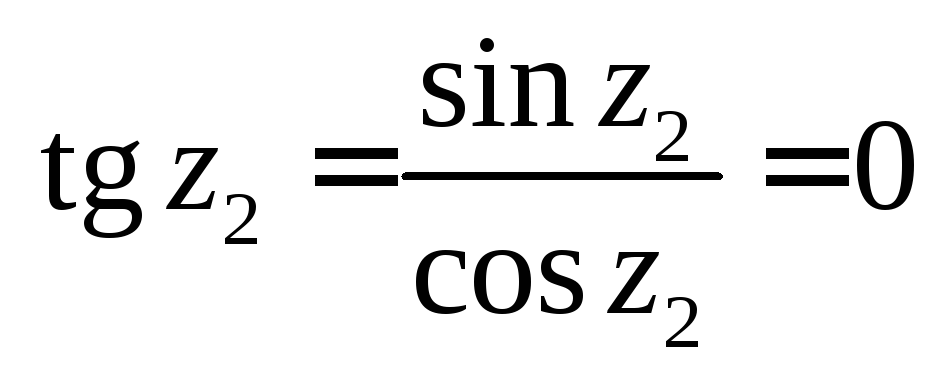Зауважимо, що приклад  7.2.2 відповідає завданню  7.2 контрольної роботи.

Література: [1, с. 278 ‑ 280], [3, с. 299 – 302], [16].

Модуль 8. Теорія ймовірностей і елементи математичної статистики

8.1. Основні поняття і теореми теорії ймовірностей

Методи теорії ймовірностей і математичної статистики служать для дослідження масових випадкових явищ. При цьому вони не дають можливості пророкувати результат кожного окремого випадкового явища. Лише в масі однорідних явищ випадкові особливості компенсуються й виявляються якісь закономірності, які й служать предметом дослідження. Сьогодні теорія ймовірностей - обов'язковий інструмент аналізу ситуацій, що включають невизначеність. Методи статистичного аналізу даних використовуються для наукових і практичних висновків в економіці, фізиці, інженерних розрахунках, у питаннях прийняття управлінських рішень та контролю якості.

Подія – це всякий факт, що може відбутися або не відбутися в результаті випробування (виконання певного комплексу умов). Наприклад, випробування - постріл, події - влучення, невлучення; випробування - однократне підкидання монети, подія - поява герба. Випадковою називається подія, що при даному комплексі умов може відбутися або не відбутися (на відміну від достовірної події, яка обов'язково відбудеться та неможливої, що не може відбутися у даному випробуванні).

Кілька подій у даному випробуванні називаються (попарно) несумісними, якщо ніякі дві з них не можуть з'явитися разом. Наприклад, виграш і програш за одним квитком лотереї; жодного влучення, одне влучення й два влучення при двох пострілах по мішені.

Кілька подій утворюють повну групу (єдино можливі події), якщо в результаті випробування хоча б одна з них обов'язково відбудеться.

Кілька подій називаються рівноможливими, якщо за умовами випробування жодну з них немає підстав вважати більш можливою, ніж інші. Наприклад, при киданні грального кубика з однорідного матеріалу внаслідок наявності симетрії жодна із граней не має переваги перед іншими. Тому події - випадання якого-небудь певного числа очок (1, 2, 3, 4, 5, 6) - будуть рівноможливими. При підкиданні симетричної монети рівноможливими є поява герба або цифри. При киданні двох монет події: – поява двох гербів (ГГ), – поява двох цифр (ЦЦ), – поява одного герба й однієї цифри (ЦГ, ГЦ) - утворять повну групу, є несумісними, але не є рівноможливими.

Дві події називаються протилежними, якщо вони несумісні й утворюють повну групу. Протилежна до подія позначається. Наприклад, поява герба або цифри при одному киданні монети, влучення й промах по мішені при одному пострілі, виграш і програш за одним квитком лотереї. Для події– випадання двох гербів при киданні двох монет – протилежною є подія– випадання хоча б однієї цифри. Якщо подія– менш двох влучень при п'ятьох пострілах, то– від двох до п'яти влучень (тобто хоча б два влучення).

Якщо події, що мають місце в результаті проведення випробування, несумісні, утворюють повну групу і рівноможливі, то вони називаються випадками, а про випробування кажуть, що воно зводиться до схеми випадків. Кожну задачу теорії ймовірностей, в якій випробування заводиться до схеми випадків, можна звести до тієї чи іншої задачі, в якій говориться про виймання куль із урни. “Задачі на урни” є свого роду єдиною мовою, на якій можна викладати найрізноманітніші за зовнішньою формою задачі.

Класичне означення ймовірності: Якщо випробування зводиться до схеми випадків, то ймовірність будь-якої події може бути обчислена за формулою

, (8.1.1)

де - загальна кількість випадків,- кількість випадків, які сприяють появі події(тобто забезпечують її появу).

Якщо – випадкова подія, то її ймовірність задовольняє нерівностям:

. (8.1.2)

Ймовірність достовірної події дорівнює одиниці, а неможливої – нулю.

Приклад 8.1.1. Кидаємо один раз монету. Обчислити ймовірність випадання герба (подія ).

Розв’язання. В цій задачі всього два випадки, . Появі подіїсприяє один випадок,. Отже, ймовірність подіїзгідно (8.1.1) дорівнює.

Приклад 8.1.2. Кидаємо 1 раз гральний кубик. Обчислити ймовірність випадання числа очок, що ділиться на 3 (подія ).

Розв’язання. Всього може бути випадків (випадання 1, 2, 3, 4, 5, 6 очок). З них лише два випадки сприяють появі події(випадання 3 і 6 очок). Отже, за формулою (8.1.1).

Приклад 8.1.3. Із урни, що містить 4 білих, 3 чорних і 7 червоних куль, виймають 1 кулю. Знайти ймовірність того, що куля виявиться білою або чорною.

Розв’язання. В цій задачі всього 14 куль (випадків), тобто . Подій (випадків), що сприяють появі події:. Отже, за формулою (8.1.1).

Безпосередній підрахунок ймовірностей буває інколи практично неможливим без застосування для попереднього обчислення значень іформул комбінаторики. При цьому важливим є уміння правильно визначати вид сполук (комбінації, розміщення, перестановки), про які йдеться в умові задачі.

Нагадаємо, що (факторіал) – це добуток натуральних чисел від 1 до, тобто

(8.1.3)

Наприклад, ,,. Вважається, що.

Кількість комбінацій (сполучень) із елементів пообчислюється за формулою:

(8.1.4)

‑ це кількість способів, якими можна обрати елементів із множини, що міститьрізних елементів (комбінації відрізняються тільки складом елементів, але не їх порядком).

Розміщення вважаються різними, якщо вони відрізняються складом елементів або порядком їх розташування. Число розміщень із пообчислюється за формулою:

(8.1.5)

У випадку, коли , розміщення називаютьсяперестановками (вони відрізняються тільки порядком елементів). Кількість перестановок для множини із елементів обчислюється за формулою:

(8.1.6)

Принцип множення – важливий принцип комбінаторики – полягає у наступному. Нехай потрібно виконати одну за іншою дій. Якщо першу дію можна виконати способами, другу –способами, і так до -ї дії, яку можна виконати способами, то всі дій можна виконати способами.

Принцип додавання: якщо дві дії взаємно виключають одна іншу, причому першу можна виконати способами, а другу – способами, то яку-небудь одну з них можна виконати способами.

Приклад 8.1.4. У партії з 30 виробів є 2 бракованих. Для контролю обрано 5 виробів. Знайти ймовірність того, що серед них буде один бракований виріб.

Розв’язання. Позначимо через подію, що полягає в появі одного бракованих виробу (і, значить, чотирьох небракованих). У цьому випадку загальна кількістьвсіх елементарних випадків випробування дорівнює кількісті комбінацій із числа всіх виробів (30) по 5, тобто. Число випадків, що сприяють появі появі події, за принципом множення дорівнює числу комбінацій із 2 (числа бракованих виробів) по 1 (число обраних бракованих виробів), помноженому на число комбінацій із 28 стандартних виробів, по 4, тобто. Тоді за формулами (8.1.1) та (8.1.4)

Приклад 8.1.5. При наборі телефонного номера абонент забув останні 3 цифри і, враховуючи те, що вони були різні, набрав їх навмання. Знайти ймовірність правильного набору потрібного номера.

Розв’язання. Позначимо через подію, що полягає в наборі вірного номера. Число випадків, що сприяють появі появі події:, бо існує лише один вірний телефонний номер. Загальна кількістьвсіх випадків випробування дорівнює числу можливих послідовностей з трьох різних цифр, які обираються із 10-ти елементної множини цифр. Таким чином,(згідно (8.1.5)). Можна було обчислитиза принципом множення: першу цифру обираємо з 10 можливих, другу – з 9, третю – з 8, що залишилися і тоді. Отже, згідно (8.1.1).

Приклад 8.1.6. Коробка містить 5 однакових за розміром занумерованих деталей. По одній навмання виймають одну за іншою всі деталі. Знайти ймовірність того, що номери вийнятих деталей розташуються в порядку зростання (подія ).

Розв’язання. Серед множини всіх можливих розташувань п’яти номерів різних деталей (що є перестановками з 5 елементів, тобто за (8.1.6) (або за принципом множення) ) лише одне розташуваннябуде сприяти появі події. Отже, згідно (8.1.1).

Приклад 8.1.7. Дехто забув п'ятизначний код до замка, але пам'ятає, що в коді по одному разу використовувалися цифри 1, 2, 3, 4, 5, і перші три були непарними. Яка ймовірність того, що при наугад набраному коді замок відкриється? (подія ).

Розв’язання. У цьому випадку загальне число всіх елементарних випадків випробування дорівнює числу перестановок з п'яти цифр, причому непарні числа можуть переставлятися тільки на перших трьох місцях, а парні – на двох останніх місцях. За принципом множення та (8.1.6) маємо:. Лише один порядок розташування цифр (а саме вірний код замка) буде сприяти появі події, тобто. Отже, за формулою (8.1.1).

При рішенні різних задач дуже часто доводиться представляти складні події у вигляді комбінації більше простих подій, використовуючи операції додавання й множення подій.

Сумою подійіназивається подія, що полягає в появі хоча б однієї події: або події, або події, або подійіодночасно.

Добутком двох подійіназивається подія, що полягає одночасній появі подійі.

Дві події називаються незалежними, якщо ймовірність однієї з них не залежить від того, відбулася інша подія чи ні. Імовірність події , знайдена за умови, що подіявже відбулася, називається умовною ймовірністю і позначається. Наприклад, якщо в цеху діють дві автоматичні лінії, не пов'язані між собою умовами виробництва, то зупинки цих ліній є незалежними подіями.

Теорема додавання ймовірностей (для несумісних подій і):

. (8.1.7)

Формула для обчислення ймовірності протилежної події:

. (8.1.8)

Теорема додавання ймовірностей (для сумісних подій і):

. (8.1.9)

Теорема множення ймовірностей (для залежних подій і):

. (8.1.10)

Теорема множення ймовірностей (для незалежних подій і):

. (8.1.11)

Імовірність появи хоча б однієї події (з подій , незалежних у сукупності):

. (8.1.12)

Приклад 8.1.8. В урні 3 білих й 2 чорних кулі. Навмання витягають дві кулі. Яка ймовірність того, що вони обидві білі?

Розв’язання. Нехай подія – першою дістали білу кулю, подія– другою дістали білу кулю.

Перший випадок ‑ урнова модель із поверненням (перша куля повертається в урну). Тоді події і– незалежні, й за (8.1.11) маємо:.

Другий випадок: урнова модель без повернення (перша куля в урну не повертається). Тоді події і– залежні, й за (8.1.10) маємо:. Імовірність появи двох білих куль (без повернення) можна знайти й у інший спосіб, за допомогою (8.1.1):.

Приклад 8.1.9. З букв розрізної абетки складене слово МАМА. Дитина розсипала ці букви, а потім навмання їх склала. Яка ймовірність того, що знову вийде МАМА?

Розв’язання. Введемо події: – з букв знову складене слово МАМА,– першою обрана картка з буквою М,– другою обрана картка з буквою А,– третьою обрана картка з буквою М,– четвертою обрана картка з буквою А. Шукана подіяполягає в спільному настанні подій,,,, тобто. Події,,,– залежні. Тому за допомогою теореми множення ймовірностей (8.1.10) маємо:

.

Приклад 8.1.10. Розрив електричного ланцюга може відбутися внаслідок виходу з ладу або першого елемента, або при одночасному виході з ладу другого й третього елементів. Елементи працюють незалежно один від іншого. Імовірності виходу з ладу елементів за певний проміжок часу відповідно дорівнюють 0,2, 0,3, 0,1. Визначити ймовірність розриву електричного ланцюга.

Розв’язання. Нехай подія – розрив електричного ланцюга, подія–-й елемент вийде з ладу (). Тоді. Події,– сумісні,,,– незалежні, та за умовою,,. Тому за теоремами додавання для сумісних подій (8.1.9) і множення для незалежних подій (8.1.11) шукана ймовірність дорівнює

Приклад 8.1.11. Один стрілець дає 80% влучень у ціль, другий – 70%, третій – 60%. Знайти ймовірність влучення в ціль хоча б одного стрільця при одночасному пострілі.

Розв’язання. Нехай подія – влучення в ціль хоча б одного стрільця,–-й стрілець влучить у ціль (). Події,,– сумісні і незалежні. За умовою,,, за формулою (8.1.8) обчислення ймовірності протилежної події:,,. Шукана ймовірність появи хоча б однієї події згідно (8.1.12) дорівнює

Наслідками теорем додавання й множення ймовірностей є формули повної ймовірності й Бейеса.

Формула повної ймовірності. Повна ймовірність події , що може відбутися лише за умови появи однієї з несумісних гіпотез, що утворюють повну групу, дорівнює

. (8.1.13)

Формули Бейеса. Імовірність гіпотези , обчислена після того, як подіявідбулася, дорівнює

. (8.1.14)

Приклад 8.1.12. Лампи надходять з трьох заводів відповідно з ймовірностями 0,5, 0,2 і 0,3. Ймовірність вийти з ладу протягом року дорівнює 0,2 для ламп, виготовлених першим заводом, 0,3 – другим і 0,1 – третім. Знайти ймовірність того, що навмання взята лампа працюватиме не менше року.

Розв’язання. Нехай подія - лампа працюватиме не менше року, гіпотези ()‑ лампа надійшла з -того заводу. Гіпотези є несумісними та єдино можливими. За умовою задачі , перевірка:.

Умовні ймовірності подій, які протилежні подіям, заданим в задачі, такі: (ймовірність того, що лампа працюватиме не менше року, якщо вона надійшла з 1-го заводу),.

Тоді за формулою повної ймовірності (8.1.13): .

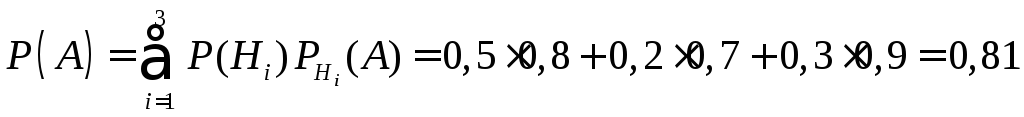Приклад 8.1.13. Виходячи із умов прикладу 8.1.12, знайти ймовірність того, що лампа, яка пропрацювала безвідмовно рік (подія ), надійшла з третього заводу. Порівняти умовні ймовірності гіпотез (‑лампа надійшла з -того заводу), тобто ймовірності гіпотез після появи події .

Розв’язання. Застосуємо формули Бейєса (8.1.14):

.

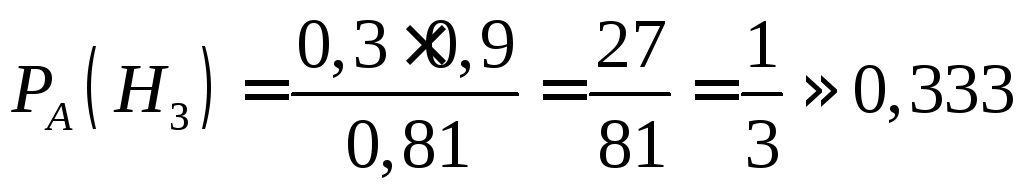- шукана ймовірність.

Перевірка: .

Одержані дані показують, що настання події спричинило зменшення ймовірностей першої та другої гіпотез та збільшення ймовірності третьої гіпотези: .

Схема Бернуллі ‑ серія із незалежних повторних випробувань, в кожному із яких ймовірність появи подіїє сталоюі не залежить від номера випробування. Тоді ймовірність події, яка полягає в тому, щоз’явитьсяразів, визначається заформулою Бернуллі:

, (8.1.15)

де - ймовірність появи подіїв одному (і кожному) випробуванні, а- ймовірність протилежної події ().

Найімовірніше число появ події в схемі Бернуллі (відповідає найбільшій ймовірності) можна знайти за допомогою подвійної нерівності:

. (8.1.16)

Формула Бернуллі є точною формулою, але її зручно застосовувати лише при не досить великій кількості випробувань . В іншому випадку застосовуються так звані асимптотичні формули, які дозволяють здійснити прийнятно наближене обчислення значень.

Так, при великих і не малих() застосовується асимптотичналокальна формула (теорема) Лапласа:

, (8.1.17)

де ,, а парна (тобто) функціятабульована (додаток А). Зауважимо також, що прибереться.

За допомогою інтегральної формули Лапласа обчислюється ймовірність того, що кількість появ міститься в інтервалі :

, (8.1.18)

де 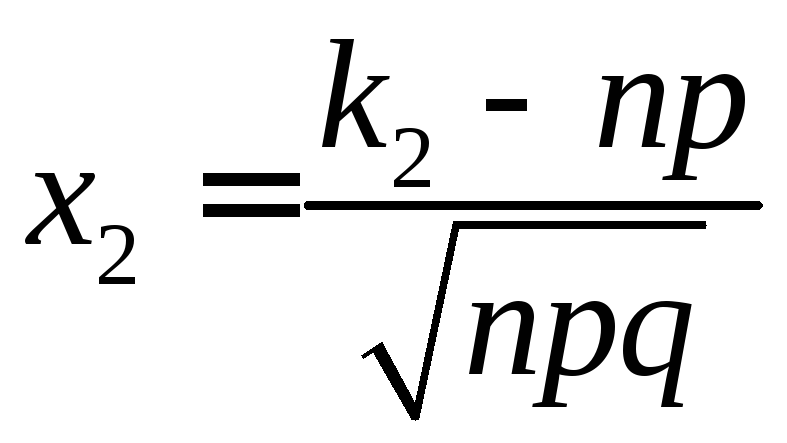. Непарнафункціятабульована (додаток Б), зазначимо також, щопри.

Асимптотична формула Пуассона ймовірностей так званих “рідких подій” використовується при великих і малих(, або):

. (8.1.19)

Додаток В містить табличні значення розподілу Пуасона (для деякіх значень ,).

Приклад 8.1.14. На підприємстві 10 машин, ймовірність виходу з ладу кожної з яких за деякий проміжок часу дорівнює 0,1. Знайти а)  ймовірність нормальної роботи підприємства, якщо для цього потрібно, щоб працювало не менше 8 машин; б) найімовірнішу кількість працюючих машин.

Розв’язання. За умовою задачі ,(ймовірність того, що машина буде працювати),(ймовірність того, що машина вийде з ладу).

а)  Робота підприємства буде нормальною, якщо у розглядуваний проміжок часу буде пряцювати або 8, або 9, або 10 машин. Ймовірність цього (за теоремою додавання ймовірностей для несумісних подій (8.1.7) ) . Використовуючи формулу Бернуллі (8.1.15) та (8.1.4) будемо мати:

.

б)  Щоб знайти найімовірнішу кількість працюючих машин, складемо подвійну нерівність (8.1.16): , тобто . Оскількиє цілим, то.

Приклад 8.1.15. На симпозіум запрошено 75 науковців, причому кожний з них прибуває з імовірністю 0,8. Яка ймовірність того, що а)  прибуде 60 чоловік; б)  число прибулих не перевищить 65?

Розв’язання. а) За умовою задачі ,,,. Шукану ймовірність обчислимо за локальною формулою Лапласа (8.1.17). Для цього спочатку знайдемо, за допомогою додатка А виписуємо табличне значення. Тоді за формулою Лапласа маємо.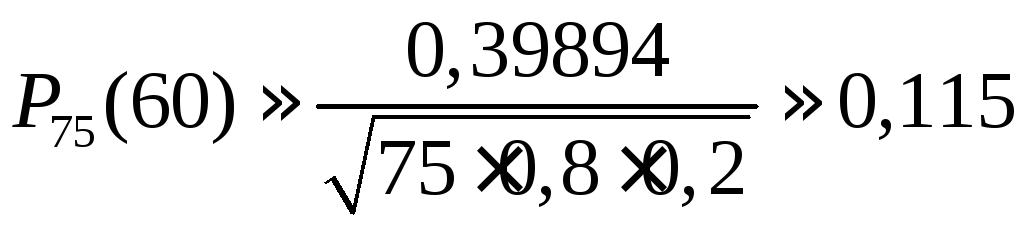

б) За інтегральною формулою Лапласа (8.1.18) знайдемо ймовірність того, що число прибулих не перевищить 65 (тобто ,):, де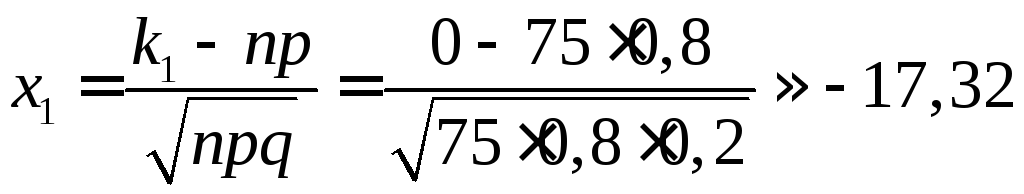,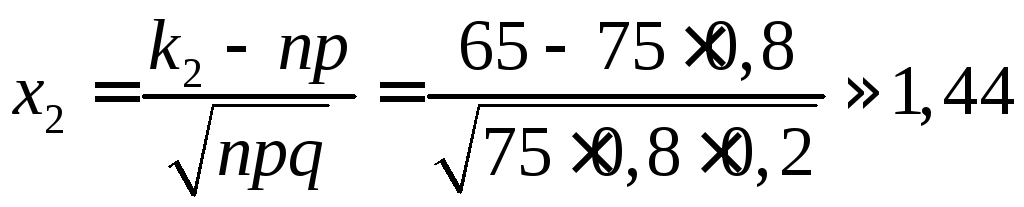. Значення функції, з огляду на її властивості, знайдемо за таблицею (додаток  Б): ;. Таким чином,.

Приклад 8.1.16. Будівельна фірма, що займається установкою літніх котеджів, розкладає рекламні листки по поштових скриньках. Колишній досвід показує, що приблизно в одному випадку із двох тисяч надходить замовлення. Знайти ймовірність того, що при розміщенні восьми тисяч листків число замовлень буде: а)  дорівнювати п'яти; б)  від двох до шести.

Розв’язання. За умовою задачі маємо ,,. Тому, отже можна застосовувати формулу Пуассона (8.1.19).

а)  За допомогою додатка В одержимо: .

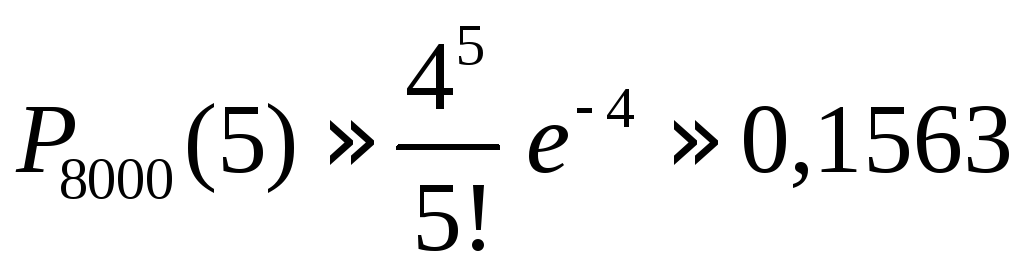б)  Шукана ймовірність . За допомогою формули Пуассона (8.1.19) та додатка В будемо мати:.

Зауважимо, що завданню 8.1 контрольної роботи відповідають:

а)  (класичне означення ймовірностей) приклади 8.1.1 – 8.1.7,

б)  (теореми додавання й множення ймовірностей) приклади 8.1.8–8.1.11,

в)  (формули повної ймовірності та Байєса) приклади 8.1.12 – 8.1.13,

г)  (схема незалежних повторних випробувань) приклади 8.1.14 – 8.1.16.

Література: [1, с. 494 ‑ 515], [4, с. 498 – 528], [16], [17], [18], [19].