
- •Міністерство освіти і науки України
- •Ббк 22.1я73
- •Правила оформлення контрольної роботи:
- •Основні питання програми
- •Модуль 1 Системи рівнянь, вектори та аналітична геометрія
- •1.1. Визначники, матриці, розв’язання систем лінійних рівнянь
- •1.2. Елементи векторної алгебри
- •1.3. Пряма на площині
- •1.4. Криві другого порядку
- •1.5. Площина та пряма в просторі
- •Модуль 2 вступ в математичний аналіз
- •2.1. Розкриття невизначеностей, і і іі визначні границі
- •2.2. Диференціальне числення функцій однієї змінної
- •Основні правила диференціювання:
- •2.3. Застосування похідних для дослідження функцій
- •2.4. Похідні в механіці
- •2.5. Диференціальне числення функцій декількох змінних
- •Модуль 3 нЕвизначений і визначений інтеграли
- •3.1. Основні методи інтегрування
- •Основні властивості невизначеного та визначеного інтегралів:
- •3.2. Невласні інтеграли
- •3.3. Застосування визначених інтегралів
- •Модуль 4 диференціальні рівняння
- •4.1. Розв’язання диференціальних рівнянь деяких типів
- •Модуль 5 кратні, криволінійні та поверхневі інтеграли
- •5.1. Подвійні, потрійні інтеграли та їх застосування
- •5.2. Криволінійні інтеграли
- •Модуль 6 числові і степеневі ряди
- •6.1. Числові ряди
- •Ознака Даламбера. Якщо для знакододатного ряду існує
- •6.2. Степеневі ряди
- •Модуль 7 комплексні числа. Елементи теорії функцій комплексної змінної
- •7.1. Комплексні числа
- •7.2. Обчислення значень елементарних функцій
- •Модуль 8. Теорія ймовірностей і елементи математичної статистики
- •8.1. Основні поняття і теореми теорії ймовірностей
- •8.2. Дискретні випадкові величини
- •8.3. Неперервні випадкові величини
- •8.4. Біноміальний та пуассонів закони розподілу
- •8.5. Нормальний, рівномірний та показниковий закони
- •Числові характеристики: , . (8.5.7)
- •8.6. Елементи математичної статистики
- •Контрольна робота № 1 Модуль 1. Системи рівнянь, вектори та аналітична геометрія
- •Модуль 2. Вступ в математичний аналіз
- •Модуль 3. Невизначений і визначений інтеграли
- •Модуль 4. Диференціальні рівняння
- •Контрольна робота № 2 Модуль 5. Кратні, криволінійні та поверхневі інтеграли
- •Модуль 6. Числові і степеневі ряди
- •Література
- •Таблиця значень функції Гаусса
- •Продовження додатка а Таблиця значень функції Гаусса
- •Додаток б Таблиця значень функції Лапласа
- •Продовження додатка б Таблиця значень функції Лапласа
- •Додаток в Значення (розподіл Пуассона)
- •Продовження додатка в Значення (розподіл Пуассона)
Ознака Даламбера. Якщо для знакододатного ряду існує
 (6.1.5)
(6.1.5)
(границя відношення наступного члена до попереднього), то
якщо
 ,
то ряд збігається;
,
то ряд збігається;якщо
 ,
то ряд розбігається;
,
то ряд розбігається;якщо
 ,
то про збіжність (розбіжність) ряду
нічого сказати не можна (слід скористатися
іншими ознаками збіжності рядів).
,
то про збіжність (розбіжність) ряду
нічого сказати не можна (слід скористатися
іншими ознаками збіжності рядів).
Цю
ознаку рекомендується використовувати,
якщо загальний член досліджуваного
ряду містить показникові або факторіальні
елементи відносно номера
![]() .
.
Радикальна
ознака Коші.
Якщо для ряду, загальний член якого
![]() ,
існує
,
існує
![]() ,
(6.1.6)
,
(6.1.6)
то
якщо
 ,
то ряд збігається;
,
то ряд збігається;якщо
 ,
то ряд розбігається;
,
то ряд розбігається;якщо
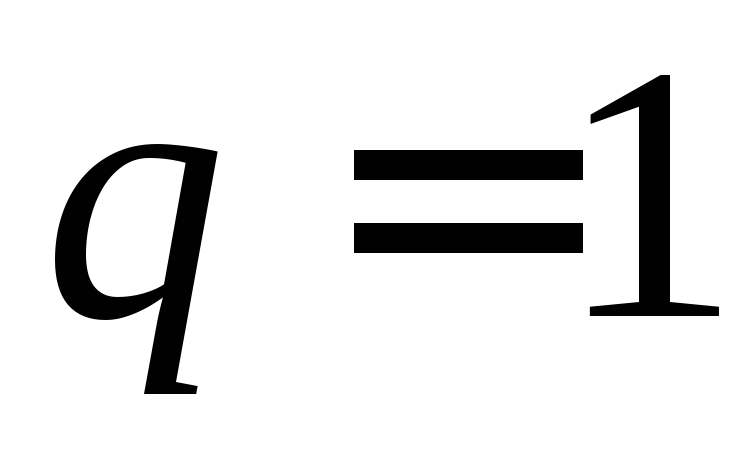 ,
то про збіжність (розбіжність) ряду
нічого сказати не можна (слід скористатися
іншими ознаками збіжності рядів).
,
то про збіжність (розбіжність) ряду
нічого сказати не можна (слід скористатися
іншими ознаками збіжності рядів).
Дану
ознаку рекомендується застосовувати,
якщо загальний член ряду є
показниково-степеневою функцією відносно
![]() .
.
Інтегральна
ознака Коші. Якщо
функція
![]() ‑ неперервна, є незростаючою і
‑ неперервна, є незростаючою і![]() при
при![]() (де
(де![]() ),
то ряд
),
то ряд збігається або розбігається одночасно
з невласним інтегралом
збігається або розбігається одночасно
з невласним інтегралом .
.
Умовам
цієї ознаки до функції
![]() задовольняєузагальнений
гармонійний ряд
задовольняєузагальнений
гармонійний ряд
 .
Через те, що невласний інтеграл
.
Через те, що невласний інтеграл =
= ,
,
то
ряд
 збігається при
збігається при![]() ,
і розбігається при
,
і розбігається при![]() .
.
Збіжність
знакопереміжних числових рядів
 досліджують заознакою
Лейбніца.
Якщо
досліджують заознакою
Лейбніца.
Якщо
розпочинаючи з деякого номера, члени ряду, взяті за абсолютним значенням, зменшуються при зростанні їх номера
 ;
; ,
,
то ряд збігається.
Приклад 6.1.1.
Дослідити
на збіжність числові ряди:
1)  ,
2)
,
2) 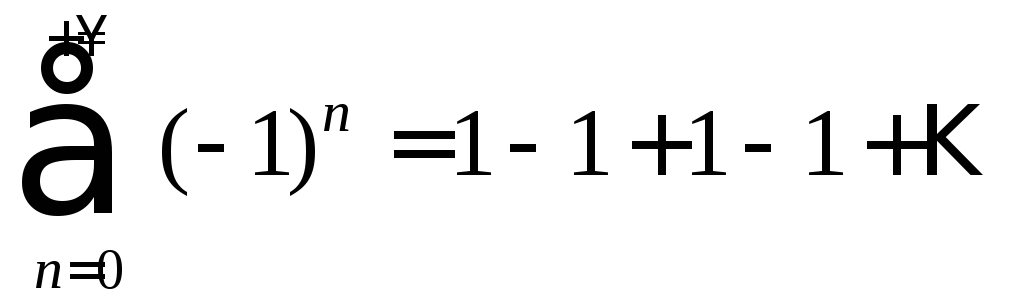 ,
3)
,
3) ,
4)
,
4) ,
5)
,
5) ,
6)
,
6) .
.
Розв’язання.
1) Обчислимо
границю загального члена
![]() ряду:
ряду:
![]() .
Ряд
.
Ряд
 розбігається,
бо необхідна умова збіжності (6.1.3) не
виконується.
розбігається,
бо необхідна умова збіжності (6.1.3) не
виконується.
2) Границя
загального члена ряду
![]() не існує, тобто необхідна умова збіжності
(6.1.3) не виконується. Значить, ряд
не існує, тобто необхідна умова збіжності
(6.1.3) не виконується. Значить, ряд
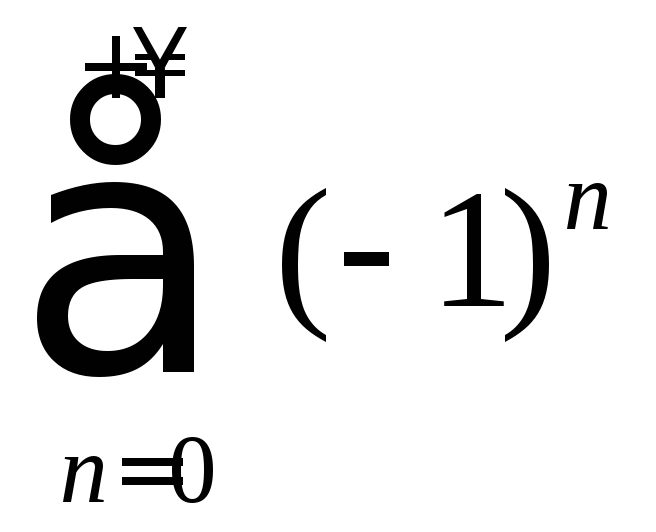 розбігається.
розбігається.
3) Ряд
 є знакододатним, бо загальний
член ряду
є знакододатним, бо загальний
член ряду
![]() (факторіал
(факторіал![]() ,
див. також розділ 8). Наступний член
,
див. також розділ 8). Наступний член ,
відношення наступного члена до
попереднього
,
відношення наступного члена до
попереднього .
Тоді границя
(6.1.5):
.
Тоді границя
(6.1.5):

![]() .
Отже, ряд розбігається за ознакою
Даламбера.
.
Отже, ряд розбігається за ознакою
Даламбера.
4) Загальний
член ряду
 .
Значить,
.
Значить,![]() ,
і границя
(6.1.6):
,
і границя
(6.1.6):
![]() .
Отже ряд
.
Отже ряд
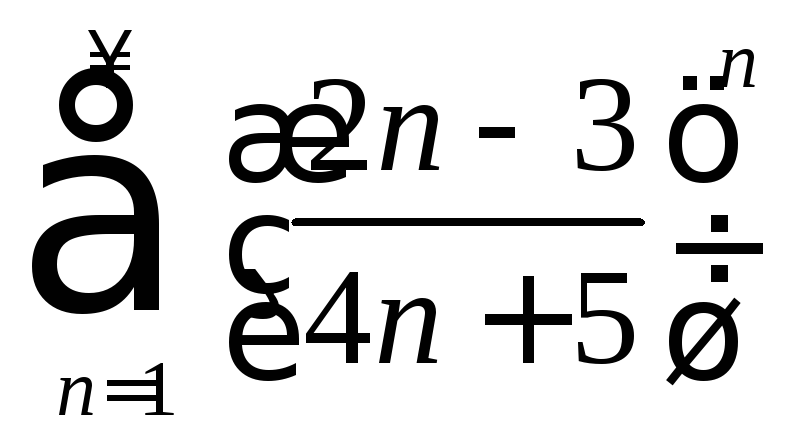 збігається
за радикальною ознакою Коші.
збігається
за радикальною ознакою Коші.
5) Порівняємо
ряд
 ізгармонійним
рядом
ізгармонійним
рядом
![]() .
.![]() ;
;![]() ,
тоді границя
(6.1.4):
,
тоді границя
(6.1.4):
 .
Отже, за граничною ознакою порівняння
досліджуваний ряд розбігається, оскільки
гармонійний ряд розбігається за
інтегральною ознакою Коші. (Можна було
застосувати інтегральну ознаку Коші
зразу до вихідного ряду).
.
Отже, за граничною ознакою порівняння
досліджуваний ряд розбігається, оскільки
гармонійний ряд розбігається за
інтегральною ознакою Коші. (Можна було
застосувати інтегральну ознаку Коші
зразу до вихідного ряду).
6) Ряд
 є знакопереміжним. Оскільки
є знакопереміжним. Оскільки![]() ,
, ,
то
,
то
![]() і
і
![]() .
Отже, досліджуваний ряд збігається
за ознакою Лейбніца.
.
Отже, досліджуваний ряд збігається
за ознакою Лейбніца.
Література: [1, с. 362 ‑ 376], [2, с. 659 ‑ 673], [4, с. 214 – 246], [15].
6.2. Степеневі ряди
Степеневий ряд
 (6.2.1)
(6.2.1)
(![]() ,
,![]() ‑ задані числа) збігається при
‑ задані числа) збігається при![]() ,
де
,
де![]() ‑ центр інтервалу (в цій точці ряд
набуває вигляду
‑ центр інтервалу (в цій точці ряд
набуває вигляду![]() ,
отже завжди збігається), а
,
отже завжди збігається), а![]() ‑ радіус збіжності
‑ радіус збіжності![]() .
Для знаходження інтервалу збіжності
степеневого ряду можна застосовувати
ознаку Даламбера, або радикальну ознаку
Коші до знакододатного ряду
.
Для знаходження інтервалу збіжності
степеневого ряду можна застосовувати
ознаку Даламбера, або радикальну ознаку
Коші до знакододатного ряду .
Наприклад, застосовуючи ознаку Даламбера
до цього ряду, отримаємо умову для
визначення інтервалу збіжності
степеневого ряду (6.2.1):
.
Наприклад, застосовуючи ознаку Даламбера
до цього ряду, отримаємо умову для
визначення інтервалу збіжності
степеневого ряду (6.2.1):
 .
(6.2.2)
.
(6.2.2)
Розв’язуючи
цю нерівність відносно
![]() ,
знаходимо інтервал збіжності
,
знаходимо інтервал збіжності
![]() .
Множина збіжності або співпадає з цим
інтервалом, або є одним із проміжків
.
Множина збіжності або співпадає з цим
інтервалом, або є одним із проміжків
![]() ,
,![]() ,
,![]() .
Якщо степеневий ряд збіжний лише при
.
Якщо степеневий ряд збіжний лише при![]() ,
то його радіус збіжності
,
то його радіус збіжності![]() .
Якщо ряд збіжний при будь-якому
.
Якщо ряд збіжний при будь-якому![]() ,
то
,
то![]() .
.
Степеневі
ряди є узагальненням багаточленів і
широко застосовуються в науці. Це
пов’язано
з можливістю представлення багатьох
функцій, зокрема всіх елементарних
функцій у вигляді сум степеневих рядів,
що називаються рядами Тейлора (Маклорена,
якщо
![]() ).
Наприклад,
).
Наприклад,
 ,
(6.2.3)
,
(6.2.3)
 ,
,
 .
(6.2.4)
.
(6.2.4)
За допомогою розкладу функцій в ряд Тейлора можна з будь-якою точністю обчислити значення функцій, інтегралів, границь і т.д. Саме на цьому грунтуються всі обчислення, що виконуються компьютерами з елементарними та спеціальними функціями.
Приклад 6.2.1.
Знайти
множину збіжності степеневих рядів:
1)  ,
2)
,
2)  ,
3)
,
3)  .
.
Розв’язання.
1) Тут
![]() ,
,![]() ‑ центр інтервалу збіжності.Оскільки
‑ центр інтервалу збіжності.Оскільки
 ,
, ,
то (при
,
то (при![]() )
)
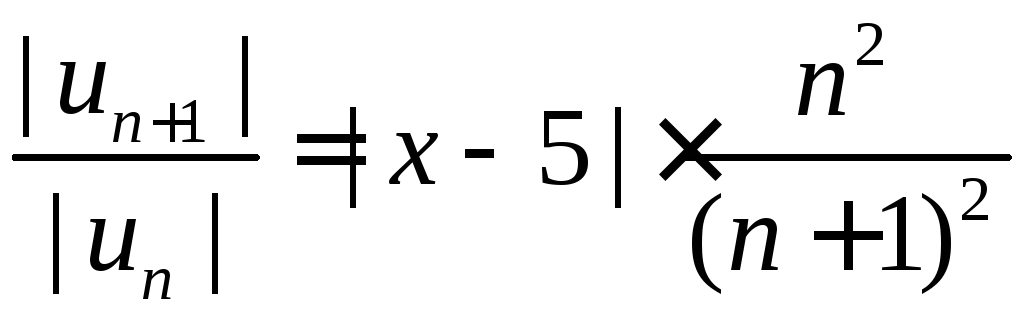 .
Значить, за ознакою Даламбера ряд
збігається, якщо
.
Значить, за ознакою Даламбера ряд
збігається, якщо .
Тобто, якщо
.
Тобто, якщо![]() ,
або
,
або![]() ,
то степеневий ряд
,
то степеневий ряд
 збігається.
До того ж за ознакою Даламбера якщо
збігається.
До того ж за ознакою Даламбера якщо
![]() ,
то ряд розбігається. Залишилось
дослідити збіжність ряду на кінцях
інтервалу (там, де
,
то ряд розбігається. Залишилось
дослідити збіжність ряду на кінцях
інтервалу (там, де![]() ).
).
При
![]() маємо знакододатний ряд
маємо знакододатний ряд ,
який збігається за інтегральною ознакою
Коші. При
,
який збігається за інтегральною ознакою
Коші. При![]() маємо знакопереміжний ряд
маємо знакопереміжний ряд ,
який збігається за ознакою Лейбніца.
Таким чином, множина збіжності ряду
являє собою відрізок
,
який збігається за ознакою Лейбніца.
Таким чином, множина збіжності ряду
являє собою відрізок![]() .
Тобто ряд
.
Тобто ряд збігається, якщо
збігається, якщо![]() ,
і розбігається, якщо
,
і розбігається, якщо![]() .
(Радіус збіжності
.
(Радіус збіжності![]() ).
).
2) Тут
![]() ,
,![]() .Оскільки
.Оскільки
![]() ,
,![]()
![]() ,
то (при
,
то (при![]() )
)
![]() .
Отже,
за
ознакою Даламбера ряд
.
Отже,
за
ознакою Даламбера ряд
 розбігається при всіх
розбігається при всіх
![]() ,
а збігається лише в точці
,
а збігається лише в точці
![]() .
(Радіус збіжності
.
(Радіус збіжності![]() ).
).
3) Тут
![]() ,
,![]() .Оскільки
.Оскільки
 ,
,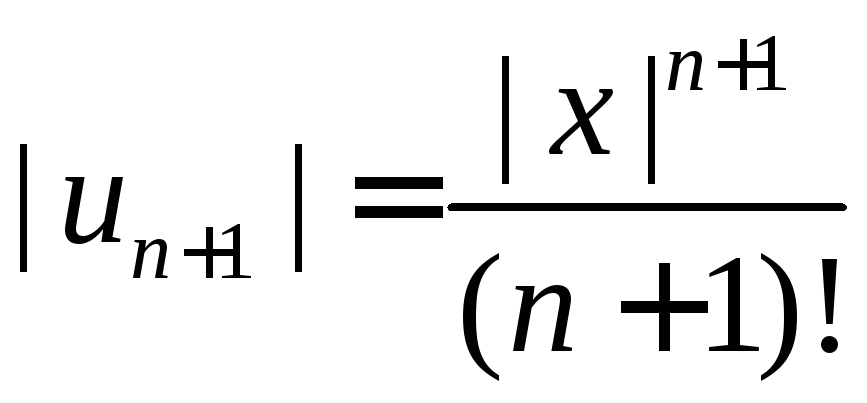 ,
то (при
,
то (при![]() )
)
 .
Отже
за
ознакою Даламбера ряд
.
Отже
за
ознакою Даламбера ряд
 збігається при всіх
збігається при всіх
![]() .
(Радіус збіжності
.
(Радіус збіжності
![]() ).
).
Література: [1, с. 377 ‑ 380], [2, с. 626 ‑ 676], [4, с. 247 – 262], [15].
