
- •Математические методы
- •Содержание
- •Раздел I
- •Тема 1. Измерения в психологии
- •Тема 2. Представление данных
- •Тема 3. Меры центральной тенденции
- •Тема 4. Меры изменчивости
- •Тема 5. Распределение признака.
- •Тема 6. Понятие выборки
- •1.2 Шкалы измерения
- •Представление данных
- •2.1 Группировка данных
- •2.2 Табулирование данных
- •2.3 Ранговый порядок
- •2.4 Распределение частот
- •2.5 Статистические ряды
- •2.6 Понятие распределения
- •Меры центральной тенденции
- •3.1 Мода
- •Замечание
- •3.2 Медиана
- •3.3 Среднее
- •3.4 Мода, медиана и среднее значение объединенных групп
- •3.5 Интерпретация моды, медианы и среднего значения
- •3.6 Выбор мер центральной тенденции
- •Меры изменчивости
- •4.1 Размах
- •4.2 Дисперсия и стандартное отклонение
- •Задача 4.1
- •Свойства дисперсии
- •Распределение признака. Нормальное распределение
- •5.1 Параметры распределения
- •5.2 Нормальное распределение
- •5.3 Асимметрия
- •5.4 Эксцесс
- •5.4 Применение нормального распределения
- •Понятие выборки
- •6.1 Полное и выборочное исследования
- •6.2 Зависимые и независимые выборки
- •6.3 Требования к выборке
- •6.4 Репрезентативность выборки
- •6.5 Формирование выборки
- •6.6 Определение объема выборки
- •Раздел II
- •Тема 7. Статистические гипотезы и
- •Тема 8. Классификация психологических
- •7.2 Статистические критерии
- •7.3 Параметрические и непараметрические методы
- •7.4 Уровни статистической значимости
- •Замечание
- •7.5 Правило отклонения нулевой и принятия альтернативной гипотезы
- •Задача 7.1
- •7.6 Мощность критериев
- •Классификация психологических задач, решаемых с помощью статистических методов
- •8.1 Классификация задач
- •Показатели группы а п Эффективность воздействия признаковризнак 1
- •После изменения
- •Показатели группы а п Степень согласованности или взаимосвязь ризнак 1
- •Показатели группы а у Сопоставление индивидуальных значений при изменении условийсловие 1
- •8.2 Принятие решения о задаче и методе
- •Раздел III
- •Тема 9. Корреляционный анализ
- •Тема 10. Выявление различий в уровне исследуемого признака
- •Тема 11. Оценка достоверности сдвига в значениях исследуемого
- •Тема 12. Критерии согласия
- •9.2 Коэффициент ранговой корреляции rS спирмена
- •9.3 Коэффициент линейной корреляции пирсона
- •9.4 Расчет уровней значимости коэффициентов корреляции
- •9.5 Коэффициент корреляции
- •Тема 10
- •Выявление различий в уровне исследуемого признака
- •10.1 Постановка задачи
- •10.2 Q – критерий розенбаума
- •10.3 S – критерий тенденций джонкира
- •Определим величину a: . Теперь определим величину b по формуле (10.11):
- •Тема 11
- •Оценка достоверности сдвига в значениях исследуемого признака
- •11.1 Постановка задачи
- •11.2 T – критерий вилкоксона
- •Типичными сдвигами в этой задаче являются сдвиги в сторону увеличения – их больше. Нетипичными – в сторону уменьшения.
- •Гипотезы к задаче
- •Тема 12
- •Выявление различий в распределении признака
- •12.1 Постановка задачи
- •12.2 2 Критерий пирсона
- •Гипотезы к задаче
- •12.3 – Критерий колмогорова-смирнова
- •12.4 Критерий * - угловое преобразование фишера
- •Гипотезы к задаче
- •Значение функции (ординаты единичной нормальной кривой)
- •Критические значения выборочного коэффициента корреляции рангов
- •Критические значения выборочного коэффициента линейной корреляции rxy Пирсона
- •Критические значения t-критерия Стьюдента при различных уровнях значимости
- •Критические значения критерия q-Розенбаума для уровней статистической значимости 0,05 и 0,01
- •Критические значения критерия s-Джонкира для количества групп (с) от трех до шести и количества испытуемых в каждой группе от двух до десяти
- •Критические значения критерия t Вилкоксона для уровней статистической значимости
- •Критические значения критерия 2 для уровней статистической значимости α 0,05 и α 0,01 при разном числе степеней свободы V
- •Критические значения dmax соответствующие уровням статистической значимости ,05 и 0,01 при сопоставлении эмпирического распределения с теоретическим
- •Таблицы для углового преобразования Фишера
- •Уровни статистической значимости разных значений критерия * Фишера
- •Лабораторные работы по дисциплине «Математические методы в психологии»
- •Лабораторная работа №1 Представление данных
- •Лабораторная работа №2 Графическое представление данных
- •Лабораторная работа № 3 Описательная статистика
- •Лабораторная работа №4 Корреляционный анализ
- •Данные для вариантов 1-6 (х1 – усредненные эталонные оценки, х2 – индивидуальные показатели преподавателя н-ва):
- •Данные для вариантов 7-12 (х1 – количество аварийных ситуаций, х2 – стаж вождения автомобиля):
- •Лабораторная работа №5 Оценка достоверности различий между двумя выборками по уровню признака
- •Данные для вариантов 7-12 (х1 – данные по детям из неблагополучных семей, х2 – данные по детям из благополучных семей):
- •Лабораторная работа №6 Оценка достоверности различий между несколькими выборками по уровню признака
- •Лабораторная работа №7 Оценка достоверности сдвига
- •Лабораторная работа №8 Оценка достоверности расхождения или согласия распределений (критерий Пирсона)
- •Лабораторная работа №9 Оценка достоверности расхождения или согласия распределений (критерий - Колмогорова-Смирнова)
- •Лабораторная работа №10 Многофункциональный критерий Фишера
- •Описание статистических функций табличного процессора Microsoft Excel
- •Частота
- •______________________________ Ранг
- •______________________________ Мин
- •______________________________ Срзнач
- •______________________________ Медиана
- •______________________________ Мода
- •______________________________ Счёт
- •______________________________ Счётесли
- •______________________________ Дисп
- •______________________________ Стандотклон
- •______________________________ Скос
- •Эксцесс
- •______________________________ Хи2тест
- •______________________________ Хи2обр
- •Применение пакета анализа для решения статистических задач в табличном процессоре Microsoft Excel
- •Корреляция
- •Литература
- •Математические методы в психологии Учебно-методическое пособие
Меры центральной тенденции
Свойства совокупности данных можно представить в форме графиков или таблиц. Часто график или таблица говорят больше, чем мы хотим или должны знать, а передаваемая информация может оцениваться временем, потребным на сообщение. Поэтому обычно используется для описания совокупности данных только два-три свойства. Эти свойства (например, «значение», наиболее часто встречающееся среди результатов, или разброс значений) могут быть описаны показателями, известными как «статистики свертки», «методы оценки средних величин» или «меры центральной тенденции».
Термин «статистики» совокупности данных используется при описании выборочной совокупности данных. Если речь идет о генеральной совокупности, то ее показатели именуются «параметрами».

3.1 Мода
Наиболее просто получаемой мерой центральной тенденции является мода. Мода – это значение во множестве наблюдений, которое встречается наиболее часто.
В совокупности значений (1, 2, 2, 7, 8, 8, 8, 10) модой является 8, потому что оно встречается чаще любого другого значения. Мода представляет собой наиболее частое значение (в данном примере 8), а не частоту этого значения (в примере равную 3).
Однако не всякая совокупность значений имеет единственную моду в строгом понимании этого определения, поэтому рабочее определение моды содержит особенности и соглашения.
В случае, когда все значения в группе встречаются одинаково часто, принято считать, что группа оценок не имеет моды. Так, в группе (0,2; 0,2; 2,3; 2,3; 4,1; 4,1) моды нет.
2. Когда два соседних значения имеют одинаковую частоту и они больше частоты любого другого значения, мода есть среднее этих двух значений. Итак, мода группы значений (0,1, 1, 2, 2, 2, 3, 3, 3, 4) равна 2,5.
3. Если два несмежных значения в группе имеют равные частоты и они больше частот любого значения, то существуют две моды. В группе значений (5, 7, 7, 7, 10, 11, 12, 12, 12, 17) модами являются и 7 и 12. В таком случае говорят, что группа оценок является бимодальной.
Замечание
Большие множества данных часто рассматриваются как бимодальные, когда они образуют полигон частот, похожий на спину бактриана – верблюда двугорбого, даже если частоты на двух вершинах не строго равны. Это незначительное искажение определения вполне оправданно, ибо термин «бимодальный»допустим и удобен для описания. Можно условиться различать большие и меньшие моды.
Наибольшей модой в группе называется единственное значение, которое удовлетворяет определению моды. Однако во всей группе может быть и несколькоменьших мод. Эти меньшие моды представляют собой, в сущности, локальные вершины распределения частот.
Например, на рисунке 3.1 наибольшая мода наблюдается при значении 6, а меньшие – при 3,5 и 10.
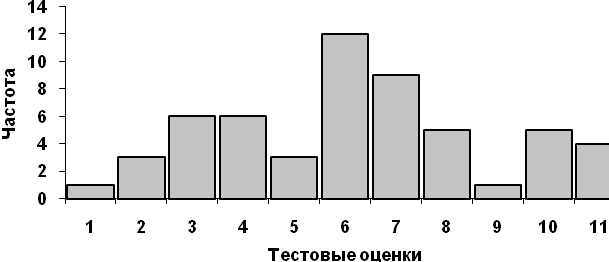
Рис. 3.1. Распределение частот тестовых оценок с наибольшей модой 6 и меньшими модами 3,5 и 10.

3.2 Медиана
Медиана (Md) –значение, которое делит упорядоченное множество данных пополам, так что одна половина значений оказывается больше медианы, а другая – меньше.
Вычисление медианы
1. Если данные содержат нечетное число различных значений, то медиана есть среднее значение для случая, когда они упорядочены. Например, в группе (17, 19, 21, 24, 27) медиана равна 21.
2. Если данные содержат четное число различных значений, то медиана есть точка, лежащая посредине между двумя центральными значениями, когда они упорядочены. В группе (3, 11, 16, 20) медиана вычисляется как (11+ 16)/2 = 13,5.
3. Если в данных есть объединенные классы, особенно в окрестности медианы, возможно, потребуется табулирование частот.
В таких случаях придется интерполировать внутри разряда значений.
Задача 3.1
Пусть, например, 36 значений, упорядоченных от 7,0 до 10,5, имеют следующее распределение:
|
Значение |
Частота |
Накопленная частота |
|
10,5 |
2 |
36 |
|
10,0 |
3 |
34 |
|
9,5 |
2 |
31 |
|
9,0 |
6 |
29 |
|
8,5 |
10=5+5 |
23 |
|
|
8 |
13 |
|
7,5 |
4 13 |
5 |
|
7,0 |
1 |
1 |
|
|
n=36 |
|
Оценкой медианы будет величина n/2, равная 18-му значению снизу. Медиана будет находиться по формуле:

(3.1)
В задаче 3.1:
фактическая нижняя граница интервала равна 8,25;
ширина интервала медианы равна 0,5;
оценка медианы n/2 = 36/2 =18;
частота, накопленная к интервалу медианы, равна13;
частота в интервале медианы равна 10.
Подставляя найденные значения в формулу (3.1), получим:
Md= 8,25 + 0,5(18-13) /10 = 8,5.


 8,0
8,0