
- •Математические методы
- •Содержание
- •Раздел I
- •Тема 1. Измерения в психологии
- •Тема 2. Представление данных
- •Тема 3. Меры центральной тенденции
- •Тема 4. Меры изменчивости
- •Тема 5. Распределение признака.
- •Тема 6. Понятие выборки
- •1.2 Шкалы измерения
- •Представление данных
- •2.1 Группировка данных
- •2.2 Табулирование данных
- •2.3 Ранговый порядок
- •2.4 Распределение частот
- •2.5 Статистические ряды
- •2.6 Понятие распределения
- •Меры центральной тенденции
- •3.1 Мода
- •Замечание
- •3.2 Медиана
- •3.3 Среднее
- •3.4 Мода, медиана и среднее значение объединенных групп
- •3.5 Интерпретация моды, медианы и среднего значения
- •3.6 Выбор мер центральной тенденции
- •Меры изменчивости
- •4.1 Размах
- •4.2 Дисперсия и стандартное отклонение
- •Задача 4.1
- •Свойства дисперсии
- •Распределение признака. Нормальное распределение
- •5.1 Параметры распределения
- •5.2 Нормальное распределение
- •5.3 Асимметрия
- •5.4 Эксцесс
- •5.4 Применение нормального распределения
- •Понятие выборки
- •6.1 Полное и выборочное исследования
- •6.2 Зависимые и независимые выборки
- •6.3 Требования к выборке
- •6.4 Репрезентативность выборки
- •6.5 Формирование выборки
- •6.6 Определение объема выборки
- •Раздел II
- •Тема 7. Статистические гипотезы и
- •Тема 8. Классификация психологических
- •7.2 Статистические критерии
- •7.3 Параметрические и непараметрические методы
- •7.4 Уровни статистической значимости
- •Замечание
- •7.5 Правило отклонения нулевой и принятия альтернативной гипотезы
- •Задача 7.1
- •7.6 Мощность критериев
- •Классификация психологических задач, решаемых с помощью статистических методов
- •8.1 Классификация задач
- •Показатели группы а п Эффективность воздействия признаковризнак 1
- •После изменения
- •Показатели группы а п Степень согласованности или взаимосвязь ризнак 1
- •Показатели группы а у Сопоставление индивидуальных значений при изменении условийсловие 1
- •8.2 Принятие решения о задаче и методе
- •Раздел III
- •Тема 9. Корреляционный анализ
- •Тема 10. Выявление различий в уровне исследуемого признака
- •Тема 11. Оценка достоверности сдвига в значениях исследуемого
- •Тема 12. Критерии согласия
- •9.2 Коэффициент ранговой корреляции rS спирмена
- •9.3 Коэффициент линейной корреляции пирсона
- •9.4 Расчет уровней значимости коэффициентов корреляции
- •9.5 Коэффициент корреляции
- •Тема 10
- •Выявление различий в уровне исследуемого признака
- •10.1 Постановка задачи
- •10.2 Q – критерий розенбаума
- •10.3 S – критерий тенденций джонкира
- •Определим величину a: . Теперь определим величину b по формуле (10.11):
- •Тема 11
- •Оценка достоверности сдвига в значениях исследуемого признака
- •11.1 Постановка задачи
- •11.2 T – критерий вилкоксона
- •Типичными сдвигами в этой задаче являются сдвиги в сторону увеличения – их больше. Нетипичными – в сторону уменьшения.
- •Гипотезы к задаче
- •Тема 12
- •Выявление различий в распределении признака
- •12.1 Постановка задачи
- •12.2 2 Критерий пирсона
- •Гипотезы к задаче
- •12.3 – Критерий колмогорова-смирнова
- •12.4 Критерий * - угловое преобразование фишера
- •Гипотезы к задаче
- •Значение функции (ординаты единичной нормальной кривой)
- •Критические значения выборочного коэффициента корреляции рангов
- •Критические значения выборочного коэффициента линейной корреляции rxy Пирсона
- •Критические значения t-критерия Стьюдента при различных уровнях значимости
- •Критические значения критерия q-Розенбаума для уровней статистической значимости 0,05 и 0,01
- •Критические значения критерия s-Джонкира для количества групп (с) от трех до шести и количества испытуемых в каждой группе от двух до десяти
- •Критические значения критерия t Вилкоксона для уровней статистической значимости
- •Критические значения критерия 2 для уровней статистической значимости α 0,05 и α 0,01 при разном числе степеней свободы V
- •Критические значения dmax соответствующие уровням статистической значимости ,05 и 0,01 при сопоставлении эмпирического распределения с теоретическим
- •Таблицы для углового преобразования Фишера
- •Уровни статистической значимости разных значений критерия * Фишера
- •Лабораторные работы по дисциплине «Математические методы в психологии»
- •Лабораторная работа №1 Представление данных
- •Лабораторная работа №2 Графическое представление данных
- •Лабораторная работа № 3 Описательная статистика
- •Лабораторная работа №4 Корреляционный анализ
- •Данные для вариантов 1-6 (х1 – усредненные эталонные оценки, х2 – индивидуальные показатели преподавателя н-ва):
- •Данные для вариантов 7-12 (х1 – количество аварийных ситуаций, х2 – стаж вождения автомобиля):
- •Лабораторная работа №5 Оценка достоверности различий между двумя выборками по уровню признака
- •Данные для вариантов 7-12 (х1 – данные по детям из неблагополучных семей, х2 – данные по детям из благополучных семей):
- •Лабораторная работа №6 Оценка достоверности различий между несколькими выборками по уровню признака
- •Лабораторная работа №7 Оценка достоверности сдвига
- •Лабораторная работа №8 Оценка достоверности расхождения или согласия распределений (критерий Пирсона)
- •Лабораторная работа №9 Оценка достоверности расхождения или согласия распределений (критерий - Колмогорова-Смирнова)
- •Лабораторная работа №10 Многофункциональный критерий Фишера
- •Описание статистических функций табличного процессора Microsoft Excel
- •Частота
- •______________________________ Ранг
- •______________________________ Мин
- •______________________________ Срзнач
- •______________________________ Медиана
- •______________________________ Мода
- •______________________________ Счёт
- •______________________________ Счётесли
- •______________________________ Дисп
- •______________________________ Стандотклон
- •______________________________ Скос
- •Эксцесс
- •______________________________ Хи2тест
- •______________________________ Хи2обр
- •Применение пакета анализа для решения статистических задач в табличном процессоре Microsoft Excel
- •Корреляция
- •Литература
- •Математические методы в психологии Учебно-методическое пособие
Распределение признака. Нормальное распределение

5.1 Параметры распределения
Распределением признаканазывается закономерность встречаемости разных его значений (Плохинский Н.А., 1970, с. 12).
Параметры распределения– это его числовые характеристики, указывающие, где «в среднем» располагаются значения признака, насколько эти значения изменчивы и наблюдается ли преимущественное появление определенных значений признака. Наиболее практически важными параметрами являются математическое ожидание, дисперсия, показатели асимметрии и эксцесса.
В реальных психологических исследованиях мы оперируем не параметрами, а их приближенными значениями, так называемыми оценками параметров. Это объясняется ограниченностью обследованных выборок. Чем больше выборка, тем ближе может быть оценка параметра к его истинному значению. В дальнейшем, говоря о параметрах, мы будем иметь в виду их оценки.
В психологических исследованиях чаще всего ссылаются на нормальное распределение.

5.2 Нормальное распределение
Нормальное распределение характеризуется тем, что крайние значения признака в нем встречаются достаточно редко, а значения, близкие к средней величине, –достаточно часто. Нормальным такое распределение называется потому, что оно очень часто встречалось в естественно-научных исследованиях и казалось «нормой» всякого массового случайного проявления признаков.
Это распределение следует закону, открытому тремя учеными в разное время: Муавром в 1733 г. в Англии, Гауссом в 1809 г. в Германии и Лапласом в 1812 г. во Франции (Плохинский Н.А., 1970, с.17). График нормального распределения представляет собой привычную глазу психолога-исследователя так называемую колоколообразную кривую.
Задача 5.1
Как оценить вероятность того, что n независимых событий с вероятностью Р получения одного из двух исходов обеспечат r удач?
Первым, кто решил эту задачу был де Муавр (1667-1754г.г.). Он пытался решить следующую задачу.
Предположим, что монета подбрасывается 10 раз. При 10 бросаниях монеты «орел» может выпасть 2 раза, а может и 8 раз. Какова вероятность того, что в результате получится 0 «орлов» или 1 «орел»?
Вероятности появления 0,1,2,…. 10 «орлов» в результате 10 бросаний монеты графически представлены на рисунке 5.1
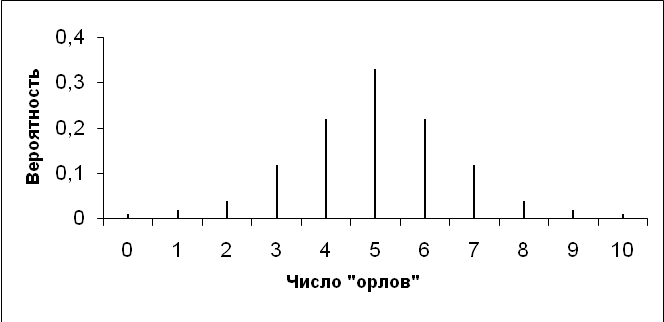
Рис.5.1. График распределения вероятности получения определенного числа «орлов» при бросаниях правильной монеты.
Задача, которую пытался решить де Муавр, состояла в том, чтобы найти уравнение кривой, близкой к данной графической интерпретации.
Де Муавру удалось показать, что искомое уравнение кривой имеет вид:
![]() ,
(5.1)
,
(5.1)
где u– высота кривой;
≈ 3,142;
е ≈ 2,718;
– соответствует среднему распределению частот выборки, определяет положение кривой относительно числовой оси;
– стандартное отклонение распределения, определяющее положение и регулирующее размах.
Графический вид нормального распределения при =0и при=1приведен на рисунке 5.2.
Такого рода кривая называется единичной нормальной кривой и имеет площадь, равную 1. Она выбрана как стандарт для нормального распределения. Меняя значения,, можно сдвигать конкретную нормальную кривую по числовой оси вверх и вниз и менять размах.
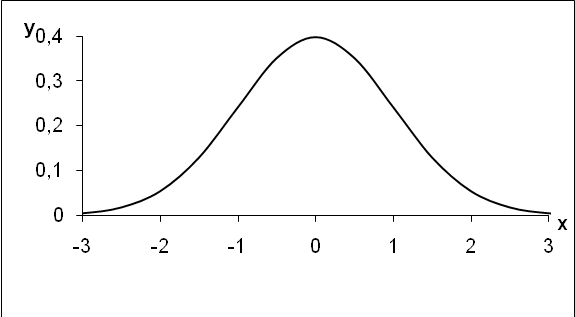
Рис.5.2. Нормальная кривая для =0и=1
На рисунке 5.3 представлен графический вид нормального распределения при =1 и разном значении, а на рисунке 5.4 графический вид нормального распределения при=0 и разном значении.
Для нахождения ординаты какого-нибудь значения единичной нормальной кривой используются специальные статистические таблицы (таблица 1 Приложения 1).
Фактически существует бесконечное множество нормальных кривых, отличающихся друг от друга значениями ,. Важное общее свойство семейства нормальных кривых заключается в доле площади между двумя точками, выраженными в стандартном отклонении:
68% площади под кривой лежит в пределах одной от среднего в любом направлении, т.е. 1;
95% площади под кривой лежит в пределах двух от среднего в любом направлении, т.е. 2;
99,7% площади под кривой лежит в пределах трех от среднего в любом направлении, т.е. 3.
=-1
=0
=1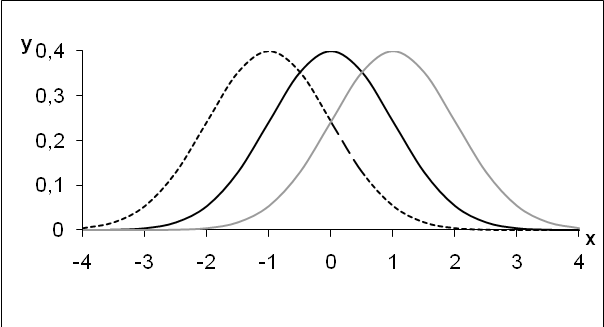
Рис. 5.3. Нормальная кривая для =1 при разном значении
=0,5
=1
=2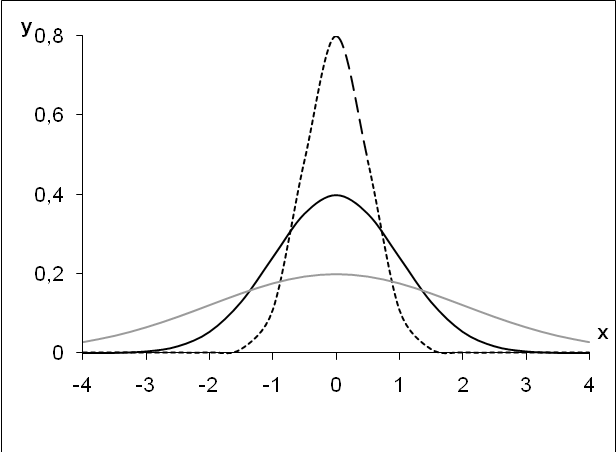
Рис. 5.4. Нормальная кривая для =0 при разном значении.

