
- •Математические методы
- •Содержание
- •Раздел I
- •Тема 1. Измерения в психологии
- •Тема 2. Представление данных
- •Тема 3. Меры центральной тенденции
- •Тема 4. Меры изменчивости
- •Тема 5. Распределение признака.
- •Тема 6. Понятие выборки
- •1.2 Шкалы измерения
- •Представление данных
- •2.1 Группировка данных
- •2.2 Табулирование данных
- •2.3 Ранговый порядок
- •2.4 Распределение частот
- •2.5 Статистические ряды
- •2.6 Понятие распределения
- •Меры центральной тенденции
- •3.1 Мода
- •Замечание
- •3.2 Медиана
- •3.3 Среднее
- •3.4 Мода, медиана и среднее значение объединенных групп
- •3.5 Интерпретация моды, медианы и среднего значения
- •3.6 Выбор мер центральной тенденции
- •Меры изменчивости
- •4.1 Размах
- •4.2 Дисперсия и стандартное отклонение
- •Задача 4.1
- •Свойства дисперсии
- •Распределение признака. Нормальное распределение
- •5.1 Параметры распределения
- •5.2 Нормальное распределение
- •5.3 Асимметрия
- •5.4 Эксцесс
- •5.4 Применение нормального распределения
- •Понятие выборки
- •6.1 Полное и выборочное исследования
- •6.2 Зависимые и независимые выборки
- •6.3 Требования к выборке
- •6.4 Репрезентативность выборки
- •6.5 Формирование выборки
- •6.6 Определение объема выборки
- •Раздел II
- •Тема 7. Статистические гипотезы и
- •Тема 8. Классификация психологических
- •7.2 Статистические критерии
- •7.3 Параметрические и непараметрические методы
- •7.4 Уровни статистической значимости
- •Замечание
- •7.5 Правило отклонения нулевой и принятия альтернативной гипотезы
- •Задача 7.1
- •7.6 Мощность критериев
- •Классификация психологических задач, решаемых с помощью статистических методов
- •8.1 Классификация задач
- •Показатели группы а п Эффективность воздействия признаковризнак 1
- •После изменения
- •Показатели группы а п Степень согласованности или взаимосвязь ризнак 1
- •Показатели группы а у Сопоставление индивидуальных значений при изменении условийсловие 1
- •8.2 Принятие решения о задаче и методе
- •Раздел III
- •Тема 9. Корреляционный анализ
- •Тема 10. Выявление различий в уровне исследуемого признака
- •Тема 11. Оценка достоверности сдвига в значениях исследуемого
- •Тема 12. Критерии согласия
- •9.2 Коэффициент ранговой корреляции rS спирмена
- •9.3 Коэффициент линейной корреляции пирсона
- •9.4 Расчет уровней значимости коэффициентов корреляции
- •9.5 Коэффициент корреляции
- •Тема 10
- •Выявление различий в уровне исследуемого признака
- •10.1 Постановка задачи
- •10.2 Q – критерий розенбаума
- •10.3 S – критерий тенденций джонкира
- •Определим величину a: . Теперь определим величину b по формуле (10.11):
- •Тема 11
- •Оценка достоверности сдвига в значениях исследуемого признака
- •11.1 Постановка задачи
- •11.2 T – критерий вилкоксона
- •Типичными сдвигами в этой задаче являются сдвиги в сторону увеличения – их больше. Нетипичными – в сторону уменьшения.
- •Гипотезы к задаче
- •Тема 12
- •Выявление различий в распределении признака
- •12.1 Постановка задачи
- •12.2 2 Критерий пирсона
- •Гипотезы к задаче
- •12.3 – Критерий колмогорова-смирнова
- •12.4 Критерий * - угловое преобразование фишера
- •Гипотезы к задаче
- •Значение функции (ординаты единичной нормальной кривой)
- •Критические значения выборочного коэффициента корреляции рангов
- •Критические значения выборочного коэффициента линейной корреляции rxy Пирсона
- •Критические значения t-критерия Стьюдента при различных уровнях значимости
- •Критические значения критерия q-Розенбаума для уровней статистической значимости 0,05 и 0,01
- •Критические значения критерия s-Джонкира для количества групп (с) от трех до шести и количества испытуемых в каждой группе от двух до десяти
- •Критические значения критерия t Вилкоксона для уровней статистической значимости
- •Критические значения критерия 2 для уровней статистической значимости α 0,05 и α 0,01 при разном числе степеней свободы V
- •Критические значения dmax соответствующие уровням статистической значимости ,05 и 0,01 при сопоставлении эмпирического распределения с теоретическим
- •Таблицы для углового преобразования Фишера
- •Уровни статистической значимости разных значений критерия * Фишера
- •Лабораторные работы по дисциплине «Математические методы в психологии»
- •Лабораторная работа №1 Представление данных
- •Лабораторная работа №2 Графическое представление данных
- •Лабораторная работа № 3 Описательная статистика
- •Лабораторная работа №4 Корреляционный анализ
- •Данные для вариантов 1-6 (х1 – усредненные эталонные оценки, х2 – индивидуальные показатели преподавателя н-ва):
- •Данные для вариантов 7-12 (х1 – количество аварийных ситуаций, х2 – стаж вождения автомобиля):
- •Лабораторная работа №5 Оценка достоверности различий между двумя выборками по уровню признака
- •Данные для вариантов 7-12 (х1 – данные по детям из неблагополучных семей, х2 – данные по детям из благополучных семей):
- •Лабораторная работа №6 Оценка достоверности различий между несколькими выборками по уровню признака
- •Лабораторная работа №7 Оценка достоверности сдвига
- •Лабораторная работа №8 Оценка достоверности расхождения или согласия распределений (критерий Пирсона)
- •Лабораторная работа №9 Оценка достоверности расхождения или согласия распределений (критерий - Колмогорова-Смирнова)
- •Лабораторная работа №10 Многофункциональный критерий Фишера
- •Описание статистических функций табличного процессора Microsoft Excel
- •Частота
- •______________________________ Ранг
- •______________________________ Мин
- •______________________________ Срзнач
- •______________________________ Медиана
- •______________________________ Мода
- •______________________________ Счёт
- •______________________________ Счётесли
- •______________________________ Дисп
- •______________________________ Стандотклон
- •______________________________ Скос
- •Эксцесс
- •______________________________ Хи2тест
- •______________________________ Хи2обр
- •Применение пакета анализа для решения статистических задач в табличном процессоре Microsoft Excel
- •Корреляция
- •Литература
- •Математические методы в психологии Учебно-методическое пособие
Тема 10

Выявление различий в уровне исследуемого признака

10.1 Постановка задачи
Очень часто перед исследователем в психологии стоит задача выявления различий между двумя, тремя и более выборками испытуемых.
Это может быть, например:
задача определения психологических особенностей хронически больных детей по сравнению со здоровыми, юных правонарушителей по сравнению с законопослушными сверстниками;
выявление различий между работниками государственных предприятий и частных фирм;
выявление различий между людьми разной национальности или разной культуры;
выявление различий между людьми разного возраста в методе «поперечных срезов».
Иногда по выявленным в исследовании статистически достоверным различиям формируется «групповой профиль» или «усредненный портрет» человека той или иной профессии, статуса, соматического заболевания и др.
В последние годы все чаще встает задача выявления психологического портрета специалиста новых профессий: «успешного менеджера», «успешного политика», «успешного торгового представителя», «успешного коммерческого директора» и др. Такого рода исследования не всегда подразумевают участие двух или более выборок. Иногда обследуется одна, но достаточно представительная выборка численностью не менее 60 человек, а затем внутри этой выборки выделяются группы более и менее успешных специалистов, и их данные по исследованным переменным сопоставляются между собой.
Сопоставление уровневых показателей в разных выборках может быть необходимой частью комплексных диагностических, учебных, психокоррекционных и иных программ. Оно помогает обратить внимание на те особенности обследованных выборок, которые должны быть учтены и использованы при адаптации программ к данной группе в процессе их конкретного воплощения.
Критерии, которые рассматриваются в данной теме, предполагают, что мы сопоставляем независимые выборки, то есть две или более выборки, состоящие из разных испытуемых. Тот испытуемый, который входит в одну выборку, уже не может входить в другую. Если мы обследуем одну и ту же выборку испытуемых, несколько раз подвергая ее аналогичным измерениям («замерам»), то перед нами – так называемые связанные, или зависимые, выборки данных.
Решение о выборе того или иного критерия в задачах этого типа принимается на основе того, сколько выборок сопоставляется и каков их объем (таблица 10.1).
Таблица 10.1
|
Количество выборок (с) |
Объемы выборок (n1 , n2 ,…) |
Методы |
|
2 |
n1 n2 и n1, n2 11 |
Q - критерий Розенбаума |
|
2 |
3 n1, n2 60 или n1=2, n2 5 |
U- критерий Манна-Уитни |
|
От 3 до 6 |
n1 = n2=…, 2 n1, n2,,… 10 |
S- критерий тенденций Джонкира |
|
3 |
{n1 , n2 , n3 } 5 |
H- критерий Крускала-Уоллиса |
|
c > 6и/илиni > 10 | ||

10.2 Q – критерий розенбаума
Назначение критерия Розенбаума
Критерий используется для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного. В каждой из выборок должно быть не менее 11 испытуемых.
Критерий позволяет быстро оценить различия между двумя выборками по какому-либо признаку. Если критерий Qне выявляет достоверных различий, это еще не означает, что их действительно нет. В этом случае стоит применить критерийφ*– Фишера. ЕслиQ – критерий выявляет достоверные различия между выборками с уровнем значимости0,01, можно ограничиться только им. Критерий применяется в тех случаях, когда данные представлены в порядковой шкале.
Гипотезы
Н0: Уровеньпризнакав выборке1не превышает уровняпризнакав выборке2.
Н1: Уровеньпризнакав выборке1превышает уровеньпризнакав выборке2.
Условия применения критерия Q –Розенбаума
Измерение может быть проведено в шкале порядка, интервалов или отношений.
Выборки должны быть независимыми.
В каждой из выборок должно быть не меньше 11 испытуемых (n1,n211 иn1 n2).
Должны соблюдаться следующие ограничения:
если n1, n2 50, то должно выполнятьсяn1 - n2 10;
если 51 n1, n2 100, то должно выполняться
n1 - n2 20
если n1, n2 100, то допускается, чтобы одна из выборок была больше другой не более чем в 1,5-2 раза.
Диапазоны разброса значений в двух выборках не должны совпадать между собой, в противном случае применение критерия бессмысленно.
Алгоритм подсчета критерия Q –Розенбаума
Проверить, выполняются ли ограничения.
Упорядочить значения отдельно в каждой выборке по степени убывания признака. Считать выборкой 1 ту выборку, значения в которой предположительно выше.
Сформулировать гипотезы.
Определить максимальное значение в выборке 2.
Подсчитать S1– количество значений в выборке 1, которые выше максимального значения в выборке 2.
Определить минимальное значение в выборке 1.
Подсчитать S2– количество значений в выборке 2, которые ниже минимального значения выборки 1.
Подсчитать эмпирическое значение критерия по формуле
Qэмп= S1 + S2. (10.1)
По таблице 5 Приложения 1определить критические значения Q для данныхn1иn2.
Для процесса принятия решения вычертить «ось значимости».
Задача 10.1
У двух групп учащихся из городской школы (14 человек) и городского лицея (12 человек), используя тест Векслера, были измерены показатели интеллекта. Можно ли утверждать, что учащиеся из городского лицея превосходят учащихся из городской школы по показателям интеллекта.
Решение
Индивидуальные показатели интеллекта по двум группам представлены в таблице 10.2 в порядке возрастания. Так как показатели в группе учащихся лицея выше, то эту группу считаем первой.
Таблица 10.2
|
№ показателей |
выборка 1 – учащиеся городского лицея |
выборка 2 – учащиеся городской школы |
|
1 |
130 |
125 |
|
2 |
128 |
125 |
|
3 |
127 |
121 |
|
4 |
127 |
112 |
|
5 |
127 |
112 |
|
6 |
126 |
100 |
|
7 |
124 |
88 |
|
8 |
124 |
84 |
|
9 |
112 |
82 |
|
10 |
112 |
78 |
|
11 |
100 |
72 |
|
12 |
100 |
|
|
13 |
99 |
|
|
14 |
94 |
|
Гипотезы к задаче
H0: Учащиеся лицея не превосходят учащихся школы по показателям интеллекта.
H1: Учащиеся лицея превосходят учащихся школы по показателям интеллекта.
Максимальный показатель во второй выборк – 125. Количество показателей первой выборки, которые больше максимального показателя второй выборки: S1 = 6.
Минимальный показатель в первой выборке – 94. Количество показателей второй выборки, которые меньше минимального показателя первой выборки: S2 = 5.
Эмпирическое значение критерия определяем по формуле (10.1):
Qэмп = S1 + S2 = 6 + 5 = 11.
По таблице определяем критические значения Qдляn1 = 14, n2 = 12:
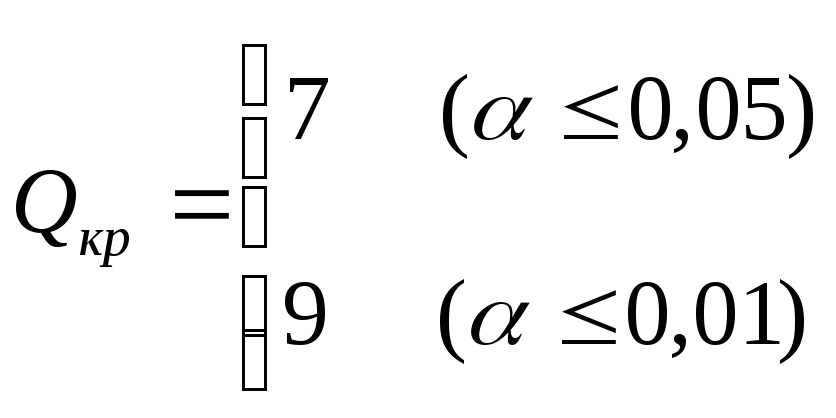 .
.
«Ось значимости»

Ответ
Qэмп=11, нулевая гипотеза отклоняется и принимается альтернативная гипотеза. Учащиеся лицея превосходят учащихся школы по показателям интеллекта(<0,01).

