
- •Математические методы
- •Содержание
- •Раздел I
- •Тема 1. Измерения в психологии
- •Тема 2. Представление данных
- •Тема 3. Меры центральной тенденции
- •Тема 4. Меры изменчивости
- •Тема 5. Распределение признака.
- •Тема 6. Понятие выборки
- •1.2 Шкалы измерения
- •Представление данных
- •2.1 Группировка данных
- •2.2 Табулирование данных
- •2.3 Ранговый порядок
- •2.4 Распределение частот
- •2.5 Статистические ряды
- •2.6 Понятие распределения
- •Меры центральной тенденции
- •3.1 Мода
- •Замечание
- •3.2 Медиана
- •3.3 Среднее
- •3.4 Мода, медиана и среднее значение объединенных групп
- •3.5 Интерпретация моды, медианы и среднего значения
- •3.6 Выбор мер центральной тенденции
- •Меры изменчивости
- •4.1 Размах
- •4.2 Дисперсия и стандартное отклонение
- •Задача 4.1
- •Свойства дисперсии
- •Распределение признака. Нормальное распределение
- •5.1 Параметры распределения
- •5.2 Нормальное распределение
- •5.3 Асимметрия
- •5.4 Эксцесс
- •5.4 Применение нормального распределения
- •Понятие выборки
- •6.1 Полное и выборочное исследования
- •6.2 Зависимые и независимые выборки
- •6.3 Требования к выборке
- •6.4 Репрезентативность выборки
- •6.5 Формирование выборки
- •6.6 Определение объема выборки
- •Раздел II
- •Тема 7. Статистические гипотезы и
- •Тема 8. Классификация психологических
- •7.2 Статистические критерии
- •7.3 Параметрические и непараметрические методы
- •7.4 Уровни статистической значимости
- •Замечание
- •7.5 Правило отклонения нулевой и принятия альтернативной гипотезы
- •Задача 7.1
- •7.6 Мощность критериев
- •Классификация психологических задач, решаемых с помощью статистических методов
- •8.1 Классификация задач
- •Показатели группы а п Эффективность воздействия признаковризнак 1
- •После изменения
- •Показатели группы а п Степень согласованности или взаимосвязь ризнак 1
- •Показатели группы а у Сопоставление индивидуальных значений при изменении условийсловие 1
- •8.2 Принятие решения о задаче и методе
- •Раздел III
- •Тема 9. Корреляционный анализ
- •Тема 10. Выявление различий в уровне исследуемого признака
- •Тема 11. Оценка достоверности сдвига в значениях исследуемого
- •Тема 12. Критерии согласия
- •9.2 Коэффициент ранговой корреляции rS спирмена
- •9.3 Коэффициент линейной корреляции пирсона
- •9.4 Расчет уровней значимости коэффициентов корреляции
- •9.5 Коэффициент корреляции
- •Тема 10
- •Выявление различий в уровне исследуемого признака
- •10.1 Постановка задачи
- •10.2 Q – критерий розенбаума
- •10.3 S – критерий тенденций джонкира
- •Определим величину a: . Теперь определим величину b по формуле (10.11):
- •Тема 11
- •Оценка достоверности сдвига в значениях исследуемого признака
- •11.1 Постановка задачи
- •11.2 T – критерий вилкоксона
- •Типичными сдвигами в этой задаче являются сдвиги в сторону увеличения – их больше. Нетипичными – в сторону уменьшения.
- •Гипотезы к задаче
- •Тема 12
- •Выявление различий в распределении признака
- •12.1 Постановка задачи
- •12.2 2 Критерий пирсона
- •Гипотезы к задаче
- •12.3 – Критерий колмогорова-смирнова
- •12.4 Критерий * - угловое преобразование фишера
- •Гипотезы к задаче
- •Значение функции (ординаты единичной нормальной кривой)
- •Критические значения выборочного коэффициента корреляции рангов
- •Критические значения выборочного коэффициента линейной корреляции rxy Пирсона
- •Критические значения t-критерия Стьюдента при различных уровнях значимости
- •Критические значения критерия q-Розенбаума для уровней статистической значимости 0,05 и 0,01
- •Критические значения критерия s-Джонкира для количества групп (с) от трех до шести и количества испытуемых в каждой группе от двух до десяти
- •Критические значения критерия t Вилкоксона для уровней статистической значимости
- •Критические значения критерия 2 для уровней статистической значимости α 0,05 и α 0,01 при разном числе степеней свободы V
- •Критические значения dmax соответствующие уровням статистической значимости ,05 и 0,01 при сопоставлении эмпирического распределения с теоретическим
- •Таблицы для углового преобразования Фишера
- •Уровни статистической значимости разных значений критерия * Фишера
- •Лабораторные работы по дисциплине «Математические методы в психологии»
- •Лабораторная работа №1 Представление данных
- •Лабораторная работа №2 Графическое представление данных
- •Лабораторная работа № 3 Описательная статистика
- •Лабораторная работа №4 Корреляционный анализ
- •Данные для вариантов 1-6 (х1 – усредненные эталонные оценки, х2 – индивидуальные показатели преподавателя н-ва):
- •Данные для вариантов 7-12 (х1 – количество аварийных ситуаций, х2 – стаж вождения автомобиля):
- •Лабораторная работа №5 Оценка достоверности различий между двумя выборками по уровню признака
- •Данные для вариантов 7-12 (х1 – данные по детям из неблагополучных семей, х2 – данные по детям из благополучных семей):
- •Лабораторная работа №6 Оценка достоверности различий между несколькими выборками по уровню признака
- •Лабораторная работа №7 Оценка достоверности сдвига
- •Лабораторная работа №8 Оценка достоверности расхождения или согласия распределений (критерий Пирсона)
- •Лабораторная работа №9 Оценка достоверности расхождения или согласия распределений (критерий - Колмогорова-Смирнова)
- •Лабораторная работа №10 Многофункциональный критерий Фишера
- •Описание статистических функций табличного процессора Microsoft Excel
- •Частота
- •______________________________ Ранг
- •______________________________ Мин
- •______________________________ Срзнач
- •______________________________ Медиана
- •______________________________ Мода
- •______________________________ Счёт
- •______________________________ Счётесли
- •______________________________ Дисп
- •______________________________ Стандотклон
- •______________________________ Скос
- •Эксцесс
- •______________________________ Хи2тест
- •______________________________ Хи2обр
- •Применение пакета анализа для решения статистических задач в табличном процессоре Microsoft Excel
- •Корреляция
- •Литература
- •Математические методы в психологии Учебно-методическое пособие
Гипотезы к задаче
Н0: Интенсивность сдвигов в сторону увеличения уровня коммуникабельности не превышает интенсивности сдвигов в сторону его уменьшения.
Н1: Интенсивность сдвигов в сторону увеличения уровня коммуникабельности превышает интенсивность сдвигов в сторону его уменьшения.
Сумма рангов нетипичных сдвигов:
Tэмп=1+2,5=3,5.
По таблице определяем критические значения Tдляn=7 (8 наблюдений уменьшаются до 7 за счет исключения показателей с нулевым сдвигом):
 .
.
Построим «ось значимости», простирающуюся в данном случае влево, т.е. слева расположена «зона значимости», а справа «зона незначимости»:
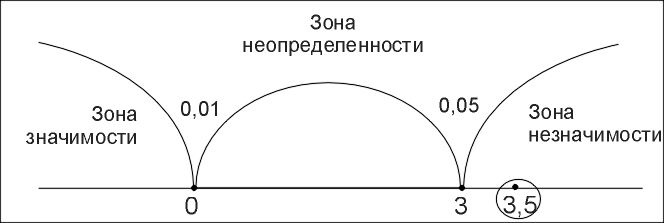
Ответ
Tэмп=3,5, принимается гипотеза H0. Интенсивность сдвигов в сторону увеличения уровня коммуникабельности не превышает интенсивности сдвигов в сторону его уменьшения. Таким образом, сдвиг в сторону увеличения коммуникативного навыка после проведения тренинга является случайным.

? ВОПРОСЫ И УПРАЖНЕНИЯ
Дайте определение сдвигу.
Дайте характеристики следующим видам сдвигов: временные, лонгитюдинальные, ситуационные, умозрительные, структурные, сдвиги под влиянием.
Охарактеризуйте понятия «уравновешенные группы» и «параллельные формы теста». Для чего они используются?
С какой целью используются исследования на контрольных группах?
Группе студентов из 20 человек были предложены два параллельных психологических теста. На первый тест студенты отвечали утром, на второй вечером, в конце учебного дня. Можно ли утверждать, что время выполнения теста влияет на конечный результат? Результаты тестирования занесены в таблицу:
-
№ испытуемого
Результат тестирования утром
Результат тестирования вечером
1
93
56
2
97
61
3
68
25
4
45
19
5
98
65
6
72
60
7
69
35
8
91
50

Тема 12

Выявление различий в распределении признака

12.1 Постановка задачи
Распределения могут отличаться по средним, дисперсиям, асимметрии, эксцессу и по сочетаниям этих параметров.
Анализ реально полученных в исследованиях распределений может позволить подтвердить или опровергнуть данные теоретического предположения. Например, сравнение распределения ответов на вопрос анкеты в двух группах людей может подчеркнуть различие этих групп или доказать их идентичность.
Если окажется, что распределения достоверно различаются, это может стать основой для классификации задач и типологии испытуемых.
Сравнение распределений может быть двух типов:
сравнение эмпирического распределения признака с теоретическим (например, с равномерным или нормальным);
сравнение эмпирических распределений признаков между собой.
Традиционные для отечественной математической статистики критерии определения расхождения или согласия распределений – это метод 2Пирсона и критерий Колмогорова-Смирнова.
Оба эти метода требуют тщательной группировки данных и довольно сложных вычислений. Кроме того, возможности этих критериев в полной мере проявляются на больших выборках. Тем не менее, они могут оказаться незаменимыми в задачах, требующих доказательства неслучайности предпочтений в выборе из нескольких альтернатив, и в задачах, требующих обнаружения точки максимального расхождения между двумя распределениями, которая затем используется для перегруппировки данных с целью применения критерия * (углового преобразования Фишера).

