
- •Математические методы
- •Содержание
- •Раздел I
- •Тема 1. Измерения в психологии
- •Тема 2. Представление данных
- •Тема 3. Меры центральной тенденции
- •Тема 4. Меры изменчивости
- •Тема 5. Распределение признака.
- •Тема 6. Понятие выборки
- •1.2 Шкалы измерения
- •Представление данных
- •2.1 Группировка данных
- •2.2 Табулирование данных
- •2.3 Ранговый порядок
- •2.4 Распределение частот
- •2.5 Статистические ряды
- •2.6 Понятие распределения
- •Меры центральной тенденции
- •3.1 Мода
- •Замечание
- •3.2 Медиана
- •3.3 Среднее
- •3.4 Мода, медиана и среднее значение объединенных групп
- •3.5 Интерпретация моды, медианы и среднего значения
- •3.6 Выбор мер центральной тенденции
- •Меры изменчивости
- •4.1 Размах
- •4.2 Дисперсия и стандартное отклонение
- •Задача 4.1
- •Свойства дисперсии
- •Распределение признака. Нормальное распределение
- •5.1 Параметры распределения
- •5.2 Нормальное распределение
- •5.3 Асимметрия
- •5.4 Эксцесс
- •5.4 Применение нормального распределения
- •Понятие выборки
- •6.1 Полное и выборочное исследования
- •6.2 Зависимые и независимые выборки
- •6.3 Требования к выборке
- •6.4 Репрезентативность выборки
- •6.5 Формирование выборки
- •6.6 Определение объема выборки
- •Раздел II
- •Тема 7. Статистические гипотезы и
- •Тема 8. Классификация психологических
- •7.2 Статистические критерии
- •7.3 Параметрические и непараметрические методы
- •7.4 Уровни статистической значимости
- •Замечание
- •7.5 Правило отклонения нулевой и принятия альтернативной гипотезы
- •Задача 7.1
- •7.6 Мощность критериев
- •Классификация психологических задач, решаемых с помощью статистических методов
- •8.1 Классификация задач
- •Показатели группы а п Эффективность воздействия признаковризнак 1
- •После изменения
- •Показатели группы а п Степень согласованности или взаимосвязь ризнак 1
- •Показатели группы а у Сопоставление индивидуальных значений при изменении условийсловие 1
- •8.2 Принятие решения о задаче и методе
- •Раздел III
- •Тема 9. Корреляционный анализ
- •Тема 10. Выявление различий в уровне исследуемого признака
- •Тема 11. Оценка достоверности сдвига в значениях исследуемого
- •Тема 12. Критерии согласия
- •9.2 Коэффициент ранговой корреляции rS спирмена
- •9.3 Коэффициент линейной корреляции пирсона
- •9.4 Расчет уровней значимости коэффициентов корреляции
- •9.5 Коэффициент корреляции
- •Тема 10
- •Выявление различий в уровне исследуемого признака
- •10.1 Постановка задачи
- •10.2 Q – критерий розенбаума
- •10.3 S – критерий тенденций джонкира
- •Определим величину a: . Теперь определим величину b по формуле (10.11):
- •Тема 11
- •Оценка достоверности сдвига в значениях исследуемого признака
- •11.1 Постановка задачи
- •11.2 T – критерий вилкоксона
- •Типичными сдвигами в этой задаче являются сдвиги в сторону увеличения – их больше. Нетипичными – в сторону уменьшения.
- •Гипотезы к задаче
- •Тема 12
- •Выявление различий в распределении признака
- •12.1 Постановка задачи
- •12.2 2 Критерий пирсона
- •Гипотезы к задаче
- •12.3 – Критерий колмогорова-смирнова
- •12.4 Критерий * - угловое преобразование фишера
- •Гипотезы к задаче
- •Значение функции (ординаты единичной нормальной кривой)
- •Критические значения выборочного коэффициента корреляции рангов
- •Критические значения выборочного коэффициента линейной корреляции rxy Пирсона
- •Критические значения t-критерия Стьюдента при различных уровнях значимости
- •Критические значения критерия q-Розенбаума для уровней статистической значимости 0,05 и 0,01
- •Критические значения критерия s-Джонкира для количества групп (с) от трех до шести и количества испытуемых в каждой группе от двух до десяти
- •Критические значения критерия t Вилкоксона для уровней статистической значимости
- •Критические значения критерия 2 для уровней статистической значимости α 0,05 и α 0,01 при разном числе степеней свободы V
- •Критические значения dmax соответствующие уровням статистической значимости ,05 и 0,01 при сопоставлении эмпирического распределения с теоретическим
- •Таблицы для углового преобразования Фишера
- •Уровни статистической значимости разных значений критерия * Фишера
- •Лабораторные работы по дисциплине «Математические методы в психологии»
- •Лабораторная работа №1 Представление данных
- •Лабораторная работа №2 Графическое представление данных
- •Лабораторная работа № 3 Описательная статистика
- •Лабораторная работа №4 Корреляционный анализ
- •Данные для вариантов 1-6 (х1 – усредненные эталонные оценки, х2 – индивидуальные показатели преподавателя н-ва):
- •Данные для вариантов 7-12 (х1 – количество аварийных ситуаций, х2 – стаж вождения автомобиля):
- •Лабораторная работа №5 Оценка достоверности различий между двумя выборками по уровню признака
- •Данные для вариантов 7-12 (х1 – данные по детям из неблагополучных семей, х2 – данные по детям из благополучных семей):
- •Лабораторная работа №6 Оценка достоверности различий между несколькими выборками по уровню признака
- •Лабораторная работа №7 Оценка достоверности сдвига
- •Лабораторная работа №8 Оценка достоверности расхождения или согласия распределений (критерий Пирсона)
- •Лабораторная работа №9 Оценка достоверности расхождения или согласия распределений (критерий - Колмогорова-Смирнова)
- •Лабораторная работа №10 Многофункциональный критерий Фишера
- •Описание статистических функций табличного процессора Microsoft Excel
- •Частота
- •______________________________ Ранг
- •______________________________ Мин
- •______________________________ Срзнач
- •______________________________ Медиана
- •______________________________ Мода
- •______________________________ Счёт
- •______________________________ Счётесли
- •______________________________ Дисп
- •______________________________ Стандотклон
- •______________________________ Скос
- •Эксцесс
- •______________________________ Хи2тест
- •______________________________ Хи2обр
- •Применение пакета анализа для решения статистических задач в табличном процессоре Microsoft Excel
- •Корреляция
- •Литература
- •Математические методы в психологии Учебно-методическое пособие
12.3 – Критерий колмогорова-смирнова
Назначение критерия
Критерий предназначен для решения тех же задач, что и критерий2. Иначе говоря, с его помощью можно сравнивать эмпирическое распределение с теоретическим или два эмпирических распределений между собой. Разница между критериями в том, что при применении2сопоставляются частоты двух распределений, а при применении критериясравниваются накопленные частоты по каждому разряду.
Критерий позволяет найти точку, в которой сумма накопленных расхождениймежду двумя распределениями является наибольшей, и оценить достоверность этого расхождения.
Если различия между двумя распределениями существенны и в какой-то момент разность накопленных частот достигнет критического значения, можно признать различия статистически достоверными. В формулу критерия включается эта разность. Чем больше эмпирическое значение, тем более существенны различия.
Гипотезы
Н0: Различия междудвумя распределенияминедостоверны (судя по точке максимального накопленного расхождения между ними).
Н1: Различия междудвумя распределениямидостоверны (судя по точке максимального накопленного расхождения между ними).
Ограничения критерия Колмогорова-Смирнова
Измерение может быть проведено в шкале интервалов и отношений.
Выборки должны быть случайными и независимыми.
Желательно, чтобы суммарный объем двух выборок был больше или равен 50.
Сопоставление эмпирического распределения с теоретическим иногда допускается при n 5.
Разряды должны быть упорядочены по нарастанию или убыванию какого-либо признака (дни недели, 1-й, 2-й, 3-й месяцы после прохождения курса терапии, повышение температуры тела, усиление чувства недостаточности и т. д.). Во всех тех случаях, когда разряды представляют собой не упорядоченные по возрастанию или убыванию какого-либо признака категории, следует применять метод 2.
Задача 12.7
В выборке учащихся одиннадцатых классов городских школ проводилось тестирование по математике. Распределение результатов тестирования представлено в таблице 12.11.
Таблица 12.11
|
Доля правильных ответов, % |
Количество учащихся, получивших результат в данном интервале |
|
0-20% |
4 |
|
21-40% |
15 |
|
41-60% |
18 |
|
61-80% |
7 |
|
81-100% |
1 |
Можно ли утверждать, что распределение результатов тестирования по математике учащихся городских школ отличается от равномерного распределения?
Решение
Н0: Эмпирическое распределение результатов тестирования по математике учащихся городских школ не отличается от равномерного распределения.
Н1: Эмпирическое распределение результатов тестирования по математике учащихся городских школ отличается от равномерного распределения.
Эмпирические частости для данного распределения рассчитываются по формуле:
![]() ,
(12.6)
,
(12.6)
где fj – частота результата в интервалеj;
n – общее количество учащихся (наблюдений).
Теоретические частости рассчитываются по формуле:
![]() ,
(12.7)
,
(12.7)
где k – количество интервалов (разрядов).
Для нашей задачи
![]() .
.
Для наглядности расчеты оформим в таблицу 12.12.
Для сопоставления накопленных эмпирических и теоретических частостей находим разность между ними и заносим ее в восьмой столбец.
Определим по восьмому столбцу, какая из абсолютных величин разности является наибольшей. Она будет обозначаться dmax. В данном случае dmax=0,222
Таблица 12.12
|
Доля правильных ответов, % |
Частота |
Частость |
Накопленная частость |
Разность | |||
|
эмпирическая |
теоретическая |
эмпирическая |
теоретическая |
эмпирическая |
теоретическая | ||
|
0-20% |
4 |
9 |
0,089 |
0,200 |
0,089 |
0,200 |
-0,111 |
|
21-40% |
15 |
9 |
0,333 |
0,200 |
0,422 |
0,400 |
0,022 |
|
41-60% |
18 |
9 |
0,400 |
0,200 |
0,822 |
0,600 |
0,222 |
|
61-80% |
7 |
9 |
0,156 |
0,200 |
0,978 |
0,800 |
0,178 |
|
81-100% |
1 |
9 |
0,022 |
0,200 |
1,000 |
1,000 |
0,000 |
|
Сумма |
45 |
45 |
1 |
1 |
|
|
0,533 |
Теперь необходимо обратиться к таблице 9 Приложения 1 для определения критических значений dmaxприn=45:
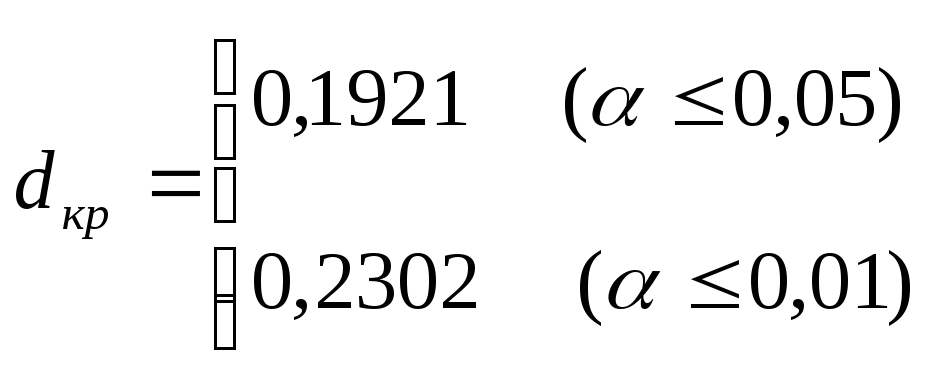 .
.
«Ось значимости»
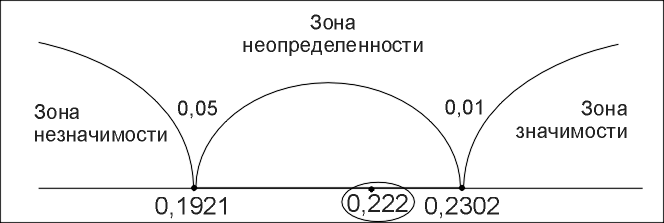
Ответ
dmax=0,222, принимаетсяН1. Эмпирическое распределение результатов тестирования по математике учащихся городских школ отличается от равномерного распределения (при<0,05).
Задача 12.8
В выборке учащихся одиннадцатых классов районных школ проводилось тестирование по математике при помощи теста, аналогичного тесту для городских школ (задача 12.7). Распределение результатов тестирования представлено в таблице 12.13.
Таблица 12.13
|
Доля правильных ответов, % |
Количество учащихся, получивших результат в данном интервале |
|
0-20% |
5 |
|
21-40% |
11 |
|
41-60% |
5 |
|
61-80% |
4 |
|
81-100% |
0 |
Можно ли утверждать, что распределение результатов тестирования по математике учащихся городских школ отличается от распределения результатов учащихся районных школ?
Решение
Гипотезы к задаче
Н0: Распределение результатов тестирования по математике учащихся городских школ не отличается от распределения результатов учащихся районных школ.
Н1:Распределение результатов тестирования по математике учащихся городских школ отличается от распределения результатов учащихся районных школ.
Поскольку в данной задаче сопоставляются накопленные эмпирические частости по каждому разряду, то теоретические частости не вычисляются.
Критерий находится по формуле:
![]() ,
(12.7)
,
(12.7)
где п1 –количество наблюдений в первой выборке;
n2– количество наблюдений во второй выборке;
dmax– наибольшее из абсолютных величин разности накопленных эмпирических частостей.
По таблице 10 Приложения 1 определить, какому уровню статистической значимости соответствует полученное значение. Если>1,36,различия между распределениями можно считать достоверными. Последовательность выборок может быть выбрана произвольно.
Основные расчеты для нашей задачи оформляются в таблицу 12.14.
Максимальная разность между накопленными эмпирическими частостями составляет 0,218 и попадает на второй разряд.
Таблица 12.14
|
Доля пра-вильных ответов, % |
Эмпирические частоты |
Эмпирические частости |
Накопленные эмпирические частости |
Разность | |||
|
|
f1 |
f2 |
f1* |
f2* |
f1* |
f2* |
f1*-f2* |
|
0-20% |
4 |
5 |
0,089 |
0,200 |
0,089 |
0,200 |
0,111 |
|
21-40% |
15 |
11 |
0,333 |
0,440 |
0,422 |
0,640 |
0,218 |
|
41-60% |
18 |
5 |
0,400 |
0,200 |
0,822 |
0,840 |
0,018 |
|
61-80% |
7 |
4 |
0,156 |
0,160 |
0,978 |
1,000 |
0,022 |
|
81-100% |
1 |
0 |
0,022 |
0 |
1,000 |
1,000 |
0 |
|
Сумма |
45 |
25 |
1 |
1 |
|
|
|
В соответствии с формулой подсчитываем эмп по формуле (12.7):
![]() .
.
По таблице 10 Приложения 1 определяем уровень статистической значимости полученного значения: =0,59.
«Ось значимости»

На оси указаны критические значения , соответствующие принятым уровням значимости:0,05=1,36,0,01=1,63.
Ответ
![]() ,
принимается H0.Распределение
результатов тестирования по математике
учащихся городских школ не отличается
от распределения результатов учащихся
районных школ.
,
принимается H0.Распределение
результатов тестирования по математике
учащихся городских школ не отличается
от распределения результатов учащихся
районных школ.

