Варианты контрольных работ

Вариант № 0

1. Найти и изобразить на чертеже область определения функции.

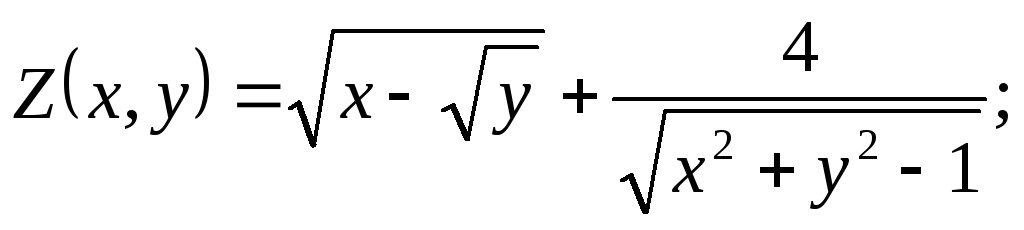
Решение. Для определения области необходимо решить следующую систему:

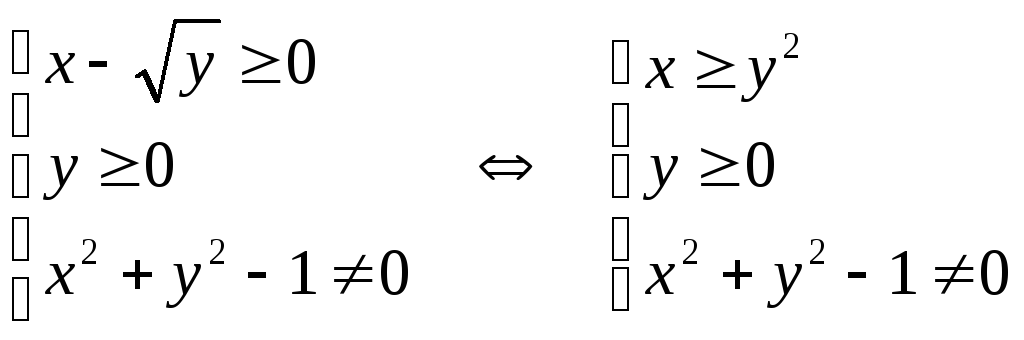
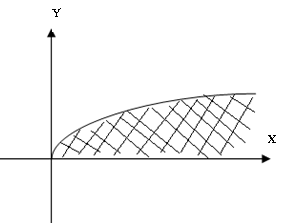
Таким образом в данном случае область определения – это область в 1-ой четверти ограниченная кривыми и удаленными из нее точками окружности

2. Показать, что заданная функция 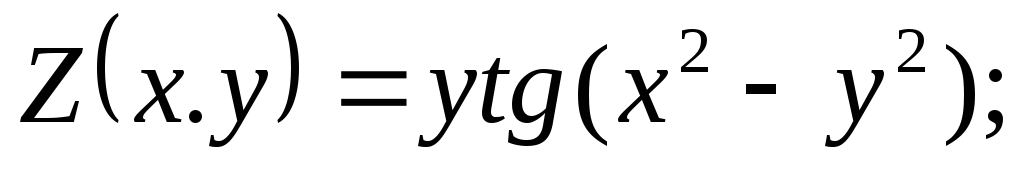удовлетворяет данному уравнению.

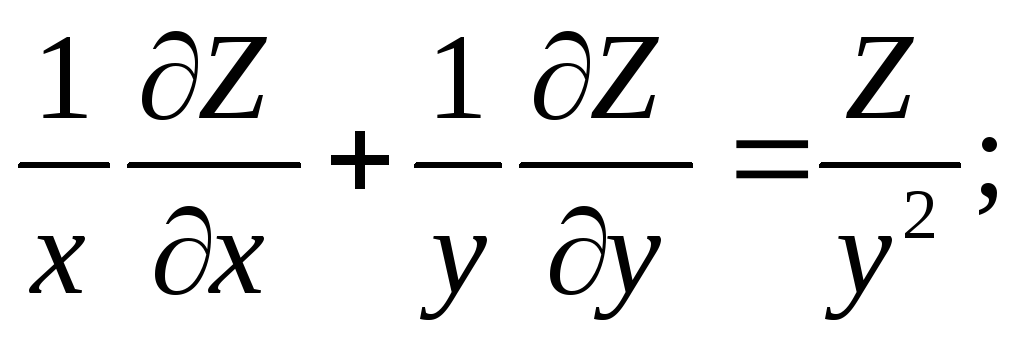
Решение. Предварительно найдем частные производные первого порядка

Подставляя, полученные производные к функцию в заданное соотношением получим

;

3. Найти производную сложной функции. ;

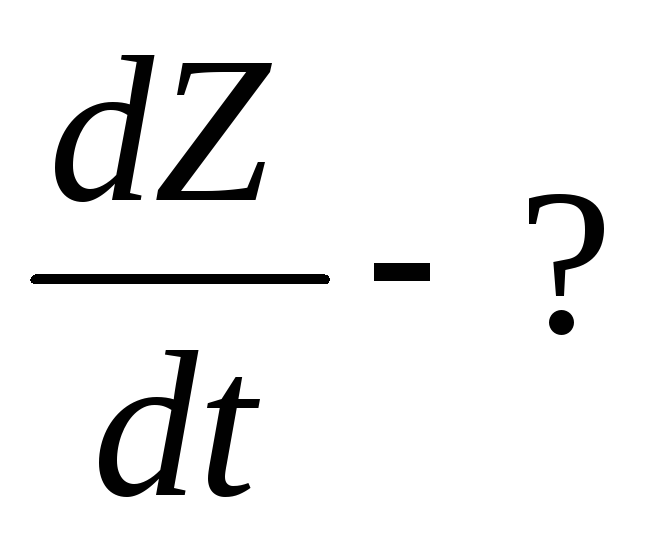
Решение. Применяя формулу для вычисление полной производной получим

Подставляя теперь вместо ивыражение черези выполняя необходимые преобразования получим

.

4. Найти экстремум функции.

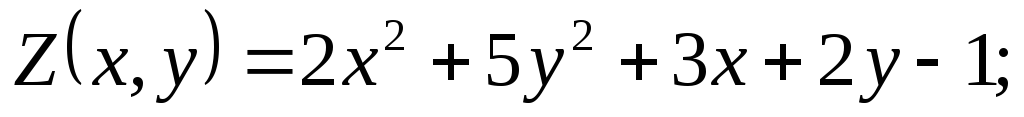
Решение. Найдем и приравняем частные производные первого порядка к нулю

Так как частные производные второго порядка являются постоянными то.

Тогда в силу достаточного условия экстркмума в точке функция имеет локальный минимум, который равен.

5. Найти наибольшее и наименьшее значения функции 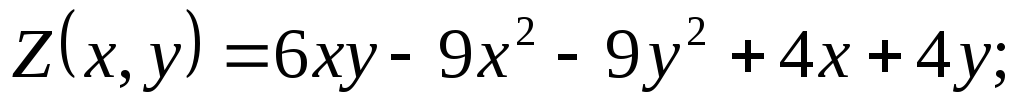в заданной замкнутой области D: .

Решение. Отметим, что границами данной области являются стороны прямоугольника, которые аналитически задаются следующим образом

Найдем и приравняем частные производные первого порядка к нулю

.

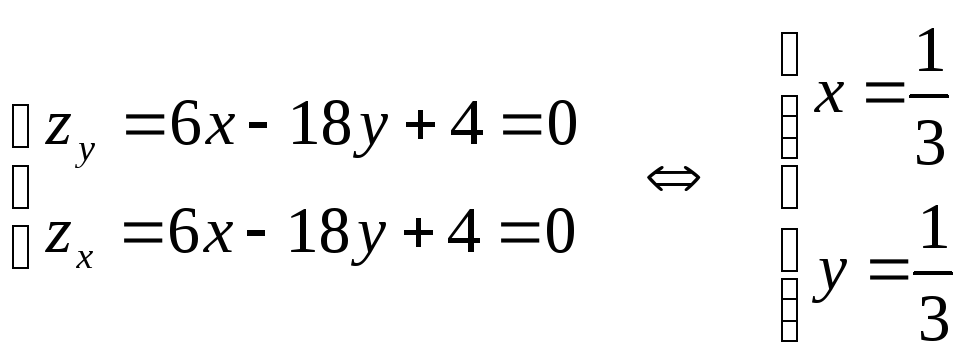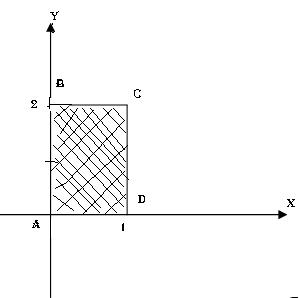
Обозначим эту точку как . Значение функции в найденной точке будет равно.

Подставляя теперь в функцию формулу границы найдем минимальные и максимальные значения на этих границах ………….…………………………………………………………………………………………………………………………………………………..

6. Найти точки условного экстремума функции.

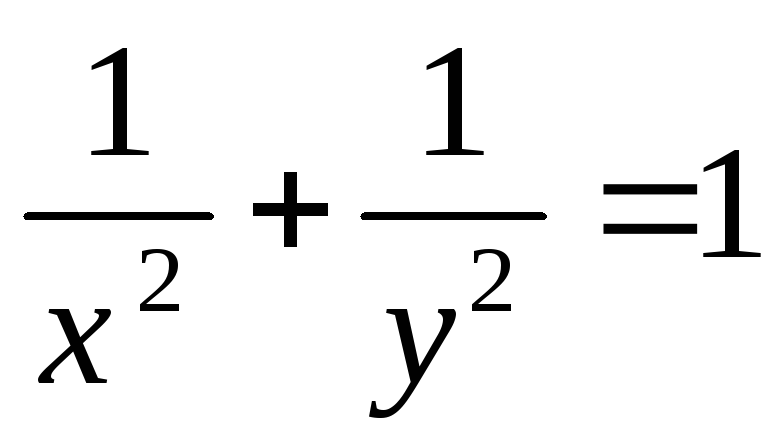
Решение. Составим функцию Лагранжа

Найдем частные производные первого порядка по переменным и приравняем их к нулю

Разрешаю указанную систему получим

Получаем две точки и. Найдем вторые производные от функции.

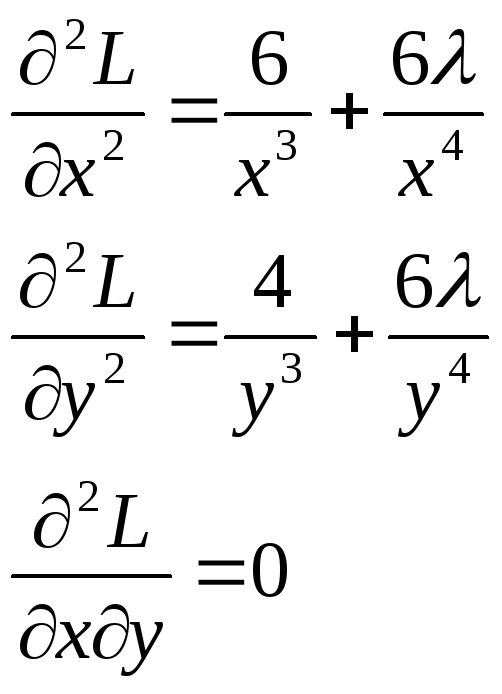
Тогда ,

Поскольку , то в точкефункция достигает локальный минимум.

Аналогично ,и, по т.ки, то в точкефункция достигает локальный максимум.

7. Составить уравнение касательной плоскости и нормали к поверхности в указанной точке .

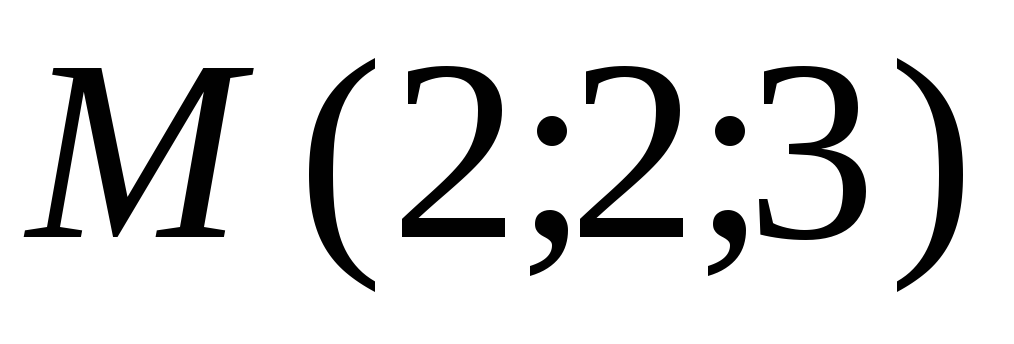Решение. Уравнение касательной плоскости, к поверхности заданным уравнением в точкезаписывается в виде:

, а уравнение нормали к поверхности в этой же точке ;

Наша поверхность задана уравнением: . Найдем частные производные

.

7. Найти производную функции в точке 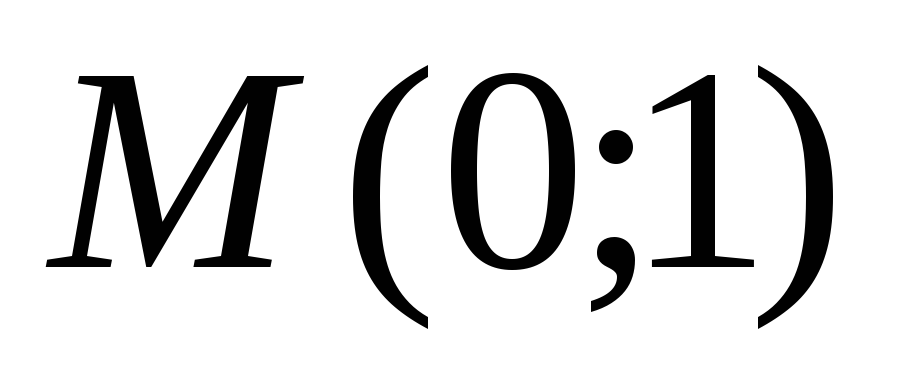в направлении:

а) градиента;

б) указанного вектора

Решение. а) Найдем частные производные первого порядка

; .

Найдем значения частной производной в точке

Тогда градиент функции найдем по формуле

.

б) Найдем направляющие косинусы:

Производную по направлению вектора найдем следующим образом:

.

Вариант 1

1. Найти и изобразить на чертеже область определения функции.

2. Показать, что заданная функция 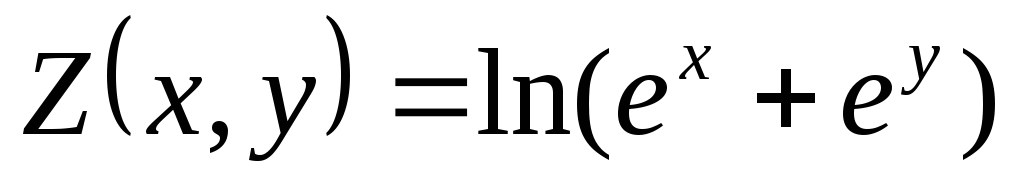удовлетворяет данному уравнению.

3. Найти производную сложной функции ;

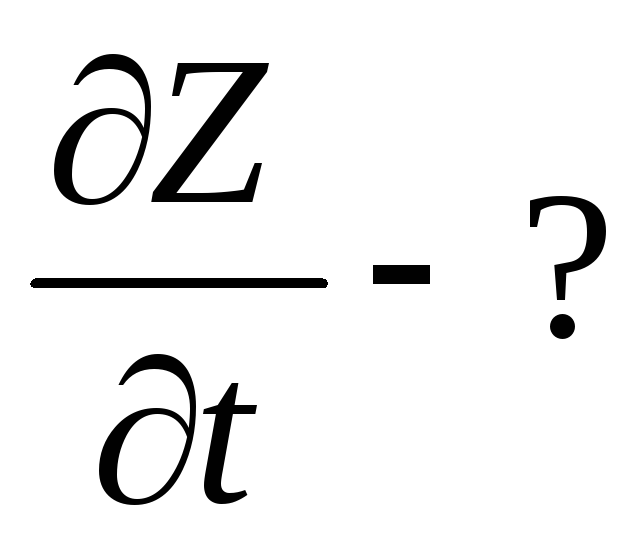
4. Найти экстремум функции.

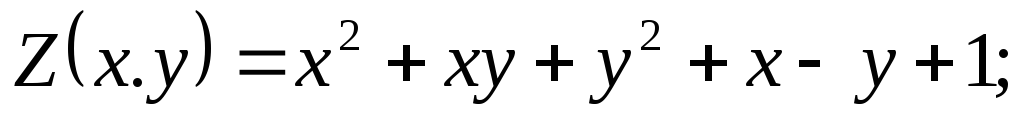
5. Найти наибольшее и наименьшее значения функции в заданной замкнутой области .

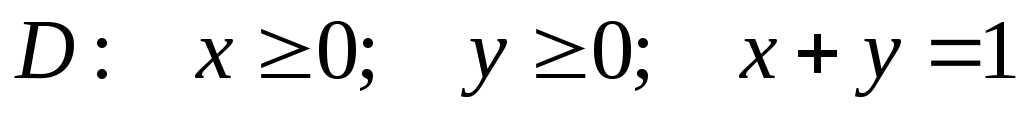6. Найти точки условного экстремума функции.

7. Составить уравнение касательной плоскости и нормали к поверхности 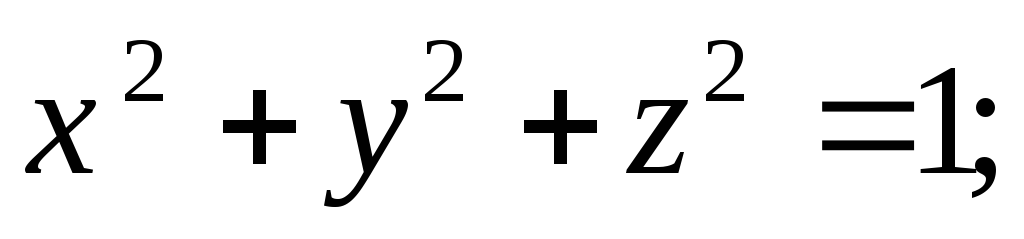в указанной точке .

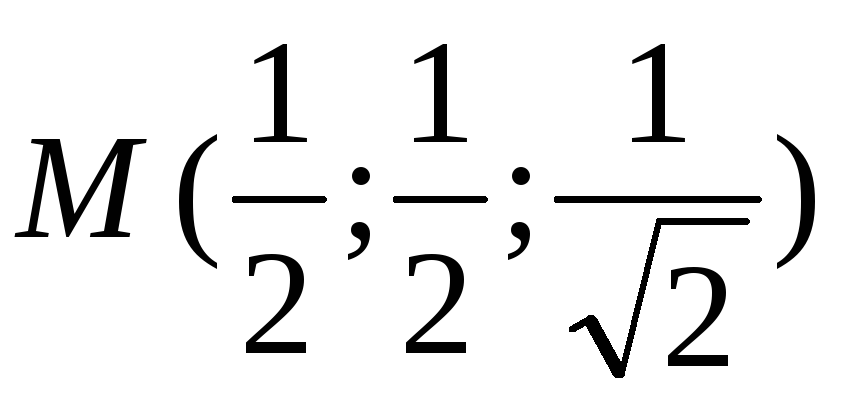8. Найти производную функции в точке в направлении:

а) градиента;

б) указанного вектора