Эксцесс

Возвращает эксцесс множества данных. Эксцесс характеризует относительную остроконечность или сглаженность распределения по сравнению с нормальным распределением. Положительный эксцесс обозначает относительно остроконечное распределение. Отрицательный эксцесс обозначает относительно сглаженное распределение.

Синтаксис

ЭКСЦЕСС(число1;число2; ...)

Число1, число2, ...   - это от 1 до 30 аргументов, для которых вычисляется эксцесс. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.

Замечания

• Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа.

• Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются.

• Если задано менее четырех точек данных или если стандартное отклонение выборки равняется нулю, то функция ЭКСЦЕСС возвращает значение ошибки #ДЕЛ/0!.

Пример

ЭКСЦЕСС(3;4;5;2;3;4;5;6;4;7) равняется -0,1518

______________________________ Хи2тест

Возвращает тест на независимость. ХИ2ТЕСТ возвращает значение для распределения хи-квадрат.  Критерий  хи-квадрат  используется для определения того, подтверждается ли гипотеза экспериментом.

Синтаксис

ХИ2ТЕСТ(фактический_интервал;ожидаемый_интервал)

Фактический_интервал   – это интервал данных, которые содержат наблюдения, подлежащие сравнению с ожидаемыми значениями.

Ожидаемый_интервал   – это интервал данных, который содержит отношение произведений итогов по строкам и столбцам к общему итогу.

Заметки

• Если фактический_интервал и ожидаемый_интервал имеют различное количество точек данных, то функция ХИ2ТЕСТ возвращает значение ошибки #Н/Д.

• Критерий  хи-квадрат сначала вычисляет  хи-квадрат  статистики, а затем ХИ2ТЕСТ возвращает вероятность для  хи-квадрат  статистики и степеней свободы df, где df = (r - 1)(c - 1).

______________________________ Хи2обр

Возвращает значение, обратное к односторонней вероятности распределения хи-квадрат. Если вероятность = ХИ2РАСП(x;...), то ХИ2ОБР(вероятность;...) = x. функция используется для сравнения наблюдаемых результатов с ожидаемыми, для того чтобы решить, была ли исходная гипотеза обоснованной.

Синтаксис

ХИ2ОБР(вероятность;степени_свободы)

Вероятность – это вероятность, связанная с распределением хи-квадрат.

Степени_свободы – это число степеней свободы.

Заметки

• Если какой-либо из аргументов не является числом, то функция ХИ2ОБР возвращает значение ошибки #ЗНАЧ!.

• Если вероятность < 0 или вероятность > 1, то функция ХИ2ОБР возвращает значение ошибки #ЧИСЛО!.

• Если степени_свободы не целое, то оно усекается.

• Если степени_свободы  <  1 или степени_свободы  ≥  10², ХИ2ОБР возвращает значение ошибки #ЧИСЛО!.

ПРИЛОЖЕНИЕ 4

Применение пакета анализа для решения статистических задач в табличном процессоре Microsoft Excel

В состав Microsoft Excel входит набор средств анализа данных (называемый пакет анализа), предназначенный для решения сложных статистических и инженерных задач. Для проведения анализа данных с помощью этих инструментов следует указать входные данные и выбрать параметры; анализ будет проведен с помощью подходящей статистической или инженерной макрофункции, а результат будет помещен в выходной диапазон. Другие инструменты позволяют представить результаты анализа в графическом виде.

Пакет анализа позволяет решать в диалоговом режиме 19 задач, наиболее часто встречающихся в классической математической статистике.

Для активизации Пакета анализа необходимо выполнить командуСервис - Надстройки и выбратьПакет анализа, после этого в менюСервис появится строкаАнализ данных.

Чтобы запустить пакет анализа:

1. в меню Сервисвыберите командуАнализ данных(рисунок 1 Приложения 1);

2. в списке Инструменты анализавыберите нужную строку;

3. введите входной и выходной диапазоны, затем выберите необходимые параметры.

Надстройки, установленные в Microsoft Excel, остаются доступными, пока не будут удалены.

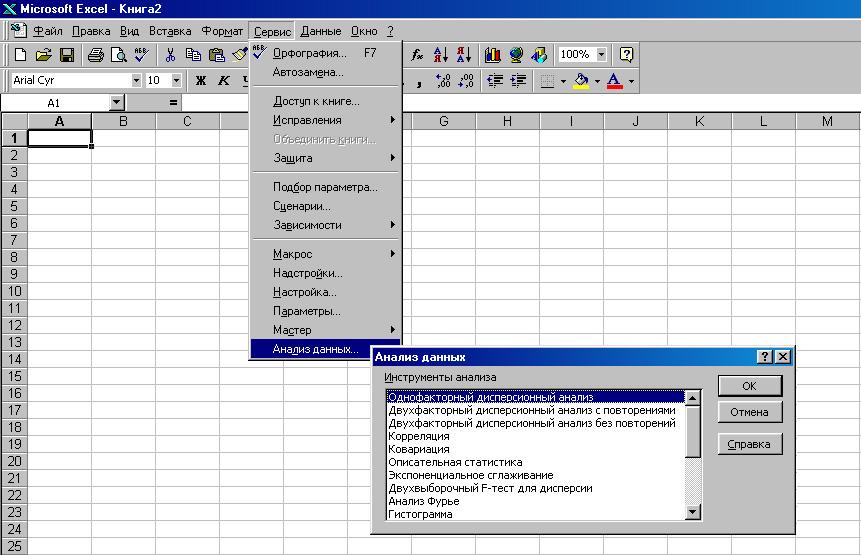
Рис.1. Инструменты анализа данных

Инструменты анализа данных:

1. однофакторный дисперсионный анализ;

2. двухфакторный дисперсионный анализ с повторениями;

3. двухфакторный дисперсионный анализ без повторений;

4. корреляция;

5. ковариация;

6. описательная статистика;

7. экспоненциальное сглаживание;

8. двухвыборочный F-тест для дисперсии;

9. анализ Фурье;

10. гистограмма;

11. скользящее среднее;

12. генерация случайных чисел;

13. ранг и персентиль;

14. регрессия;

15. выборка;

16. парный двухвыборочный t-тест для средних;

17. двухвыборочный t-тест с одинаковыми дисперсиями;

18. двухвыборочный t-тест с различными дисперсиями;

19. двухвыборочный z-тест для средних.

Рассмотрим применение инструментов анализа данных: Описательной статистикииКорреляции.

Описательная статистика

Описательная статистика применяется для генерации одномерного статистического отчета, содержащего информацию о центральной тенденции и изменчивости входных данных.

Алгоритм применения инструмента Описательная статистика:

1. Установите входной диапазон - ссылку на ячейки, содержащие анализируемые данные. Ссылка должна состоять как минимум из двух смежных диапазонов данных, организованных в виде столбцов или строк.

2. Выберите форму группирования По столбцамилиПо строкам.

3. Установите переключатель для создания заголовков.

4. Установите флажок, если в выходную таблицу необходимо включить строку для уровня надежности. В поле введите требуемое значение. Например, значение 95% вычисляет уровень надежности среднего со значимостью 0,05.

5. Установите флажок, если в выходную таблицу необходимо включить строку для k-го наибольшего значения для каждого диапазона данных. В соответствующем окне введите числоk. Еслиkравно 1, эта строка будет содержать максимум из набора данных.

6. Установите флажок, если в выходную таблицу необходимо включить строку для k-го наименьшего значения для каждого диапазона данных. В соответствующем окне введите числоk. Еслиkравно 1, эта строка будет содержать минимум из набора данных.

7. Укажите выходной диапазон.

8. Установите флажок, если в выходном диапазоне необходимо получить по одному полю для каждого из следующих видов статистических данных.

На рисунке 2 Приложения 4 представлено заполненное диалоговое окно, в котором в параметре «Входной интервал» указан диапазон с исходными значениями ряда X.

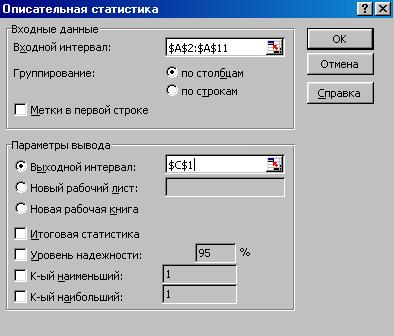
Рис. 2. Диалоговое окно инструмента Описательная статистика.

Результаты применения инструмента Описательная статистикапредставлены на рисунке 3 Приложения 4.

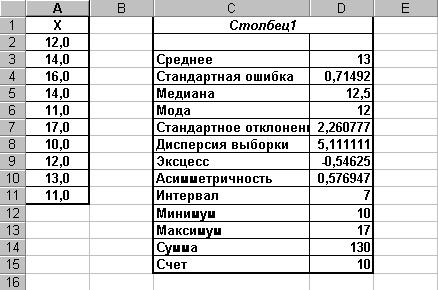
Рис. 3. Результаты применения инструмента Описательная статистика.