12.4 Критерий * - угловое преобразование фишера

Многофункциональные статистические критерии – это критерии, которые могут использоваться по отношению к самым разнообразным данным, выборкам и задачам. С помощью этого рода критериев можно решать задачи на сопоставление уровней исследуемого признака, сдвигов и сравнение распределений. При этом данные могут быть представлены в любой шкале, выборки могут быть независимые и связанные.

К многофункциональным статистическим критериям относятся угловое преобразование Фишера (^*критерий Фишера), применяемое в случае наличия двух выборок, и биноминальный критерийmдля задач с одной выборкой.

Применение многофункциональных критериев позволяет определить, какая доля наблюдений в данной выборке характеризуется интересующим нас эффектом и какая доля этим эффектом не характеризуется.

В качестве эффектов могут выступать:

• качественные признаки (выражение согласия с предложением, выбор правой дорожки из двух и т.д.);

• количественные признаки (уровень оценки, превышающий проходной балл, решение задачи менее чем за 20 секунд и т.п.);

• соотношение значений или уровней признаков (преимущественное появление крайних признаков).

Назначение критерия ^*

Критерий Фишера предназначен для сопоставления двух выборок по частоте встречаемости интересующего исследователя эффекта.

Критерий оценивает достоверность различий между процентными долями двух выборок, в которых зарегистрирован интересующий исследователя эффект.

Суть углового преобразования Фишера состоит в переводе процент­ных долей в величины центрального угла, который измеряется в радианах. Большей процентной доле будет соответствовать больший угол , меньшей доле – меньший угол,но соотношения здесь нелинейные:

,

где Р– процентная доля, выраженная в долях единицы.

При увеличении расхождения между углами ₁и₂и увеличении численности выборок значение критерия возрастает. Чем больше величина^*, тем более вероятно, что различия достоверны.

Критерии ^* используется часто в сочетании с критерием  Колмогорова-Смирнова в целях достижения максимально точного результата.

Гипотезы

Н₀: Доля лиц, у которых проявляетсяисследуемый эффект, ввыборке 1не больше, чем ввыборке 2.

Н₁: Доля лиц, у которых проявляетсяисследуемый эффект, ввыборке 1больше, чем ввыборке 2.

Условия применения критерия ^*

1. Измерение может быть проведено в любой шкале.

2. Характеристики выборок могут быть любыми.

3. Ни одна из сопоставляемых долей не должна быть равной нулю.

4. Нижняя граница – в одной из выборок может быть только 2 наблюдения, при этом во второй должно быть не менее 30 наблюдений. Верхняя граница не определена.

5. Должны соблюдаться следующие соотношения в численности двух выборок:

• если n₁ =2, тоn₂ 30;

• если n₁ =3, тоn₂ 7;

• если n₁ =4, тоn₂ 5;

• если n₁ 5, тоn₂ 5 (любые сочетания).

Задача 12.8

Психолог провел эксперимент, в котором выяснилось, что из 20 учащихся с экспериментальной задачей справились 11 (55%) человек, а из 25 человек второй группы успешно справились с задачей 10 (40%). Различаются ли две группы учащихся по успешности решения новой экспериментальной задачи?

Решение

Гипотезы к задаче

Н₀: Доля лиц, справившихся с задачей, в первой группе не больше, чем во второй.

Н₁: Доля лиц, справившихся с задачей, в первой группе больше, чем во второй.

По таблице 11 Приложения 1 находим величины ₁и₂, соответствующие процентным долям в каждой группе:

_1(55%)=1,671,

_2(40%)=1,369.

Подсчитаем эмпирическое значение ^*по формуле (12.8):

, (12.8)

где ₁ – угол, соответствующий большей процентной доле;

₂ – угол, соответствующий меньшей процентной доле;

n₁ – количество наблюдений в выборке 1;

n₂ – количество наблюдений в выборке 2.

В нашем случае

.

По таблице 12 Приложения 1 определяется, что = 1,007 соответствует уровню значи­мости>0,10.

Можно установить и критические значения , соответствующие принятым в психологии уровням статистической значимости:

.

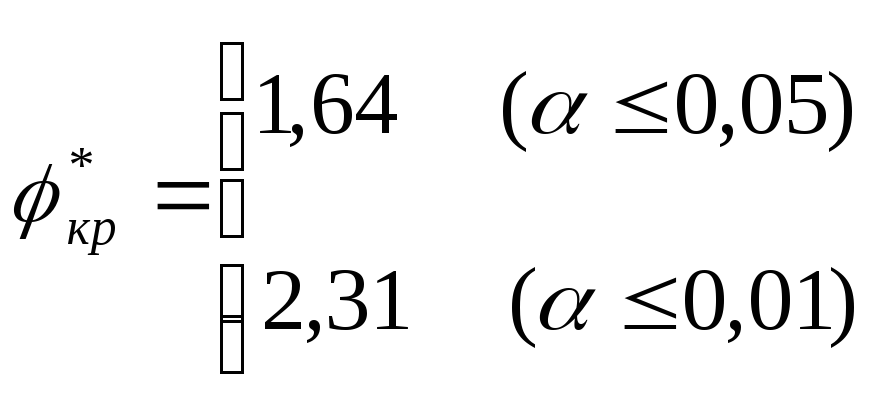«Ось значимости»

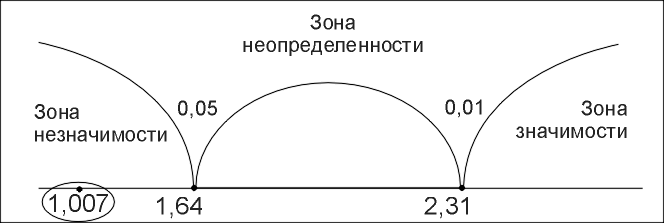
Ответ

= 1,007, принимается H₀. Доля лиц, справившихся с задачей, в первой группе не больше, чем во второй.

Критерий Фишера с равным успехом может использоваться и при сравнении распределений количественных признаков. В данном варианте использования критерия сравнивается про­цент испытуемых в одной выборке, которые достигают определенного уровня значения признака, с процентом испытуемых, достигающих этого уровня, в другой выборке.

Задача 12.9

Будет ли уровень тревожности у подростков-сирот более высоким, чем у сверстников из полных семей?

Для решения этой задачи психолог проводил анализ выраженности уровня тревожности в группе сирот и в группе детей из полных семей при помощи опросника Тейлора. 40 баллов и выше рассматривались как показатель высокой тревожности (Практическая психодиагностика: Методики и тесты. – Изд-во БАХРАХ-М.2000.С.164)

Решение

В первой группе из 10 человек очень высокий уровень тревожности наблюдался у 7 испытуемых (70%), во второй группе из 13 человек он был обнаружен у 3 испытуемых (23,1%). Можно ли считать подобные различия статистически значимыми?

Гипотезы к задаче

Н_о: Доля лиц с высоким уровнем тревожности, в первой группе детей не больше, чем во второй.

Н₁: Доля лиц с высоким уровнем тревожности, в первой группе детей больше, чем во второй.

По таблице 11 Приложения 1 определяем величины , соответствующие процентным долям «эффекта» в каждой из групп:

_1(70%)=1,982 ,

_2(23,1%)=1,003.

Подсчитываем по формуле (12.8):

.

Критические величины этого критерия нам уже известны:

.

«Ось значимости»

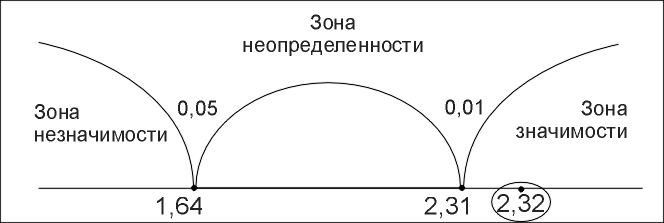
Ответ

= 2,32, принимается H₁. Доля лиц с высоким уровнем тревожности, в первой группе детей больше, чем во второй.

Если выборки сопоставляются по каким-либо количественно измеренным показателям, встает проблема выявления той точки распределения, которая может использоваться как критическая при разделении всех испытуемых на тех, у кого «есть эффект», и тех, у кого «нет эффекта».

Для того чтобы максимально повысить мощность критерия ^*, нужно выбрать точку, в которой различия между двумя сопос­тавляемыми группами являются наибольшими. Точнее всего мы сможем сделать это с помощью алгоритма расчета критерия, позволяющего обнаружить точку максимального расхождения между двумя выборками.

Рассмотрим задачу, демонстрирующую использование критерия ^* в сочетании с критерием  Колмогорова-Смирнова.

Задача 12.10

Рассмотрим решение задачи 12.8 с момента определения максимальной разности между двумя накопленными эмпириче­скими частостями.

Максимальная разность d_max=0,218 оказывается накопленной во второй категории результатов. Попробуем использовать верхнюю границу данной категории в качестве критерия для разделения обеих выборок на подгруппу, где «есть эффект», и подгруппу, где «нет эффекта».

Будем считать, что «эффект есть», если данный учащийся получил результат от 41 до 100%, и «эффекта нет», если данный учащийся получил от 0 до 40%.

Полученное распределение результатов пред­ставлено в таблице 12.16:

Таблица 12.16

Доля правильных ответов, %	Эмпирические частоты выбора данной категории результата
	Учащиеся городских школ (n1=45)	Учащиеся районных школ (n2=25)	Суммы
от 0 до 40%	19	16	35
от 41 до 100%	26	9	35
Суммы	45	25	70

Полученную таблицу мы можем использовать, проверяя разные гипотезы путем сопоставления любых двух ее ячеек.

Доля лиц, получивших результат в пределах от 41 до 100%, среди учащихся городских школ составляет 57,8% (26/45=0,578), среди учащихся районных школ – 36% (9/25=0,36).

Для применения критерия *переформулируем вопрос в нашей задаче: можно ли считать, что доля учащихся, получивших результат в пределах 41-100%, среди учащихся городских школ больше, чем среди учащихся районных школ?