6.33.Материальная точка движется по гиперболе ху=2 так, что ее абсцисса х равномерно возрастает со скоростью 1 м/с. С какой скоростью изменяется ордината точки, когда она проходит положение (6, 2)?

6.34.Исходя из определения производной, доказать, что: а) производная периодической дифференцируемой функции есть функция периодическая; б)производная четной дифференцируемой функции есть функция нечетная; в)производнаянечетнойдифференцируемойфункцииестьфункциячетная.

6.35. Доказать, что если функция f (x) дифференцируема в точке x = 0 и

f (0)= 0 , то f ′(0)= lim f (x).

x→0 x

6.36. Исследоватьнепрерывностьидифференцируемостьфункции y =| x |3 приx=0. 6.37. Функция y =| sin x | непрерывна при любом х. Убедиться, что при х=0 она недифференцируема. Имеются ли другие значения независимой

переменной, при которых функция недифференцируема?

6.38.Исследовать непрерывность и дифференцируемость функции y = e− x .

6.39.Найти f ′(0), если f (x)= x(x +1)...(x +1234567).

6.2. Дифференцирование функций

При нахождении производной функции y = f (x) обычно используют правила дифференцирования и таблицу производных основных элементарных функций.

Основные правиладифференцирования.

1.Если функции u = f (x) и v = g(x) имеют производные в точке x0, то

вэтой точке существуют производные суммы, разности, произведения и частного этих функций (частного – при условии, что g(x0 ) ≠ 0 ), причем в

точке x0 справедливы равенства:

2. Постоянный множитель k выносится за знак производной

(ku)′ = k u′.

3. Производная постоянной равна нулю: C′ = 0.

195

Пример 6.7. Вычислить производную функции y = (3x3 − 2x +1) sin x .

Решение. Функция представляет собой произведение двух функций, поэтому следует применить правило дифференцирования произведения, а затем правило дифференцирования суммы и табличные производные степенной функции и синуса:

=(3x3 − 2x +1)' sin x + (3x3 − 2x +1) (sin x)' =

=(9x2 − 2) sin x + (3x3 − 2x +1) cos x .

Решение. Функция представляет собой частное, поэтому применяем правило дифференцирования частного и формулу производной степенной функции (для x = x1/2 и для x2 ):

Подставляем в найденное выражение значение x=2:

196

Производная сложной функции. Если функция y = g(x) имеет производную в точке x0 , а функция z = f (y) имеет производную в точке y0 = g(x0 ), то сложная функция z = F(x) = f (g(x)) имеет производную в точке x0 и

F′(x0 ) = f ′(y0 )g′(x0 ).

Интерпретация этой формулы такова: скорость F′(x0 ) изменения переменной z по отношению к скорости изменения переменной x равна произведению скоростей f ′(y0 ) и g′(x0 ) (если y растет быстрее x в k раз, а z – быстрее y в m раз, то z растет быстрее x в k ×m раз).

Пример 6.10. Найти производную сложной функции y = u2 +3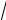u −1, если u = x4 +1.

Решение. По правилу дифференцирования сложной функции получаем

Пример 6.11. Найти производную функции y= ex2 .

Решение. Представим функцию y= ex2 в виде суперпозиции двух функций y = eu и u = x2 . Имеем y′x = yu′ u′x = (eu )'u (x2 )'x = eu 2x . Подставляя x2

вместо u, получим y = 2xex2 .

Пример 6.12. Найти производную функции y=ln sin x.

Пример 6.13. Найти производную функции y = tg 12 x .

197

Решение. Случай сложной функции, полученной в результате нескольких суперпозиций, исчерпывается последовательным применением правила

воспользоваться формулой для производной сложной функции f '(x) = (ln(tg(3x ) + x3))' = (tg(3x ) + x3 )' =(*).

Далее к числителю полученного выражения применяем формулу производной суммы, а функцию tg(3x )также дифференцируем как сложную с использованием табличных производных тангенса и показательной функции:

2 x4 + x3 +5 2 x4 + x3 +5

198

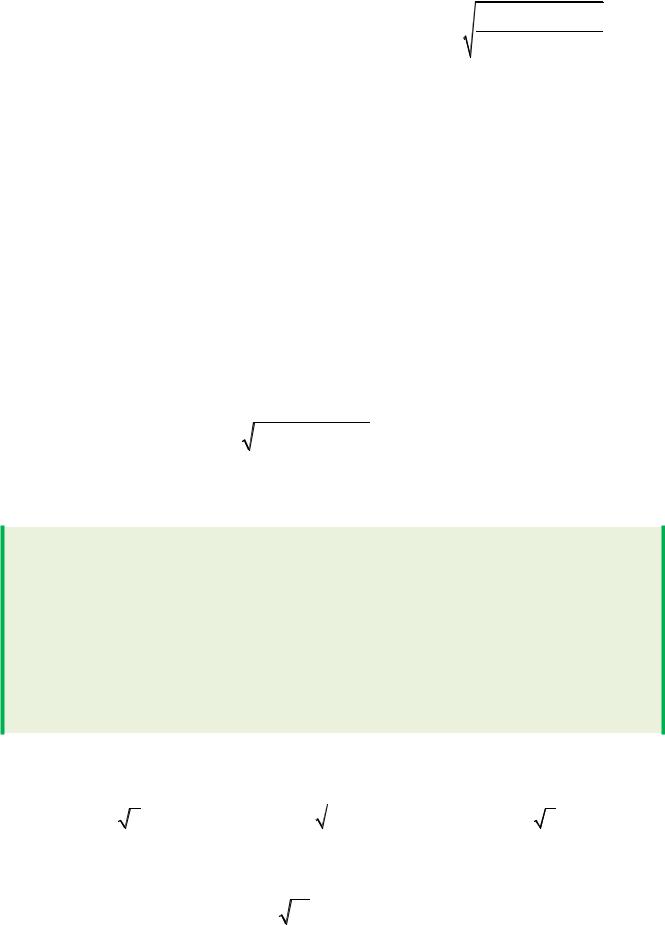
Пример 6.16. Найти производную функции y = ln 3 (x2 + 4)5(3x -1)x7 .

(6x3 +1)2 etg 5

Решение. Преобразуем исходное выражение, используя свойства логарифмов

Дифференцируя обе части последнего равенства, получим:

y0 = f (x0 ), строго монотонна, непрерывна и имеет производную в точке y0 :

199

Таким же образом могут быть получены все формулы для производных arcctg x, arcsin x, arccos x и других обратных функций, приведенных в таблице производных.

Логарифмическое дифференцирование. Пусть функция f (x) принимает положительные значения и дифференцируема на некотором интервале. Тогда по формуле производной сложной функции производная от логарифма

f (x) . В экономике еееще называют темпом изменения функции.

Способ логарифмического дифференцирования состоит в том, что сначала находят логарифмическую производную функции, а затем – производную самой функции по формуле

Эту формулу удобно использовать в тех случаях, когда производную натурального логарифма данной функции найти проще, чем производную самой функции. Например:

200

Пример 6.19. Найти производную функции y = x2 ex2 ln x cos2 x .

Решение. Прологарифмируем обе части равенства. По свойствам

Производная показательно-степенной функции. У показательной функции независимая переменная входит в показатель степени, у степенной переменная является основанием. Если же функция представляет собой степень, основание и показатель которой зависят от переменной, то такую функцию называют показательно-степенной. Общий вид такой функции: y = u(x)v(x) , или кратко: y = uv .

При нахождении производной показательно-степенной функции можно каждый раз применять технику логарифмического дифференцирования или

201

Пример 6.21. Найти производную функции f (x) = (x2 +3x)x cos x .

Решение. Воспользуемся правилом дифференцирования показательно-

Дифференцирование функций, заданных параметрически. Если

функция y = f (x) задана в параметрическом виде: x =ϕ(t) , причем функция

y =ψ (t)

φ(t) монотонна и имеет обратную функцию t=Φ(x), то у=ψ(Φ(х)) и y′(x) =ψ′(t)Φ′(x) =ψ′(t)ϕ′1(t) = xy′′((tt)) .

Другими словами, производная от параметрически заданной величины y по независимой переменной х равна отношению производных от y и от х,

взятых по параметру t. Таким образом, производную функции, заданной параметрически, можно находить без определения непосредственной зависимости у от х.

Пример 6.23. Даны параметрические уравнения кривой, называемой циклоидой x = a (1−cost), y = a t− t( Найти производную y′(x) .

Решение. Дифференцируем x и y по параметру t

202