38. Discharge with varying head (emptying of vessels)

Let us investigate efflux of a liquid through an orifice or tube in the bottom of an open vessel with a discharge coefficient JLI (Fig. 92). The discharge in this case takes place with a varying, gradually decreasing head, i.e., the flow is, strictly speaking, unsteady.

However, if the head and, consequently, the velocity of discharge are changing slowly, the motion at any given instant can be regarded as steady and Bernoulli's equation can be applied for problem solution.

Let h be the falling elevation of the free surface above the bottom, S the cross-sectional area of the vessel at that elevation and So the area of the orifice. Then, taking a differential time interval dt, the volume equation can be written as follows

(9.15)

or

where dh = fall of free surface in the vessel in time dt.

The minus sign is due to the fact that the positive increment dt corresponds to a negative increment dh.

From this, assuming μ = const, the total time of emptying a vessel of height H can be found in the

(9.16)

The integral can be computed if the law of change of the area S is known as a function of the height h. If the surface area of the vessel is uniform, i. e., S = const,

or

(9.17)

The numerator is equal to twice the volume of the vessel, the denominator represents the rate of discharge at the initial moment, i.e., when thehead was H. Consequently, the time of emptying the vessel is twice the time that would have been required if the initial head were maintained.

Equations (9.16) and (9.17) can also be used to determine the time needed to fill a vessel when the head varies from h = H to h = 0 as the vessel is filled.

Aeronautical engineers usually have to deal with discharge from closed vessels (tanks) connected with the atmosphere by an orifice or tube of small diameter (Fig.93). In this case liquid efflux causes a vacuum in the tank and atmospheric air flows in through the orifice. As a result, the discharge is retarded, the retardation being the greater the greater the resistance to the penetration of air into the tank.

To determine the time it takes for such a vessel to empty, two Bernoulli equations must be written: one for the flow of air from the motionless atmosphere into the vessel, another for the motion of the liquid from the free surface to its outlet into the atmosphere. Using the notation of Fig.93,

The compressibility of the air can be neglected and the volume rates of discharge of the air and the liquid can be equated:

(If the jet contracts, the coefficient e, should be introduced.) The foregoing equations can now be rewritten as follows:

Adding these equations and solving for Q yields

(9.18)

Substituting Eq. (9.18) into the volume equation (9.15), solving for dt and integrating from h = H to h = 0, we obtain

(9.19)

This formula is valid for the case of air intake and liquid outflow through pipes, introducing the following expression for the respective loss coefficients:

whereI and d are the length and diameter of the pipe, respectively; £f = sum of the local loss coefficients in the pipe.

Another example of discharge with varying head is found in the operation of an undercarriage shock-absorber. A hydropneumatic shock-absorber (Fig. 94) contains compressed air at the upper end the pressure of which during flight is p₀. When the airplane wheels touch the ground the hydraulic fluid flows through an orifice of area S_o and discharge coefficient μ, and the air is compressed to p₁. The height of the air volume is reduced from h₀ to h₁.

To simplify the actual process of shock-absorption, assume that a uniform force G is suddenly applied to the shock-absorber and that the air compresses according to an iso-thermic law. Let us find the duration of the shock-absorption process, i.e., the time it takes for the liquid to flow through the orifice until equilibrium is restored.

By analogy with Eq. (9.15),

Sdh = — Qdt_y

where 5 = piston area;

dh = displacement of cylinder in time dt.

The rate of discharge through the orifice

where is the constant pressure over the piston;

p = the varying air pressure given by the isothermal equation

Substitution of the expressions for p_x and p into Eq. (9.15) yields

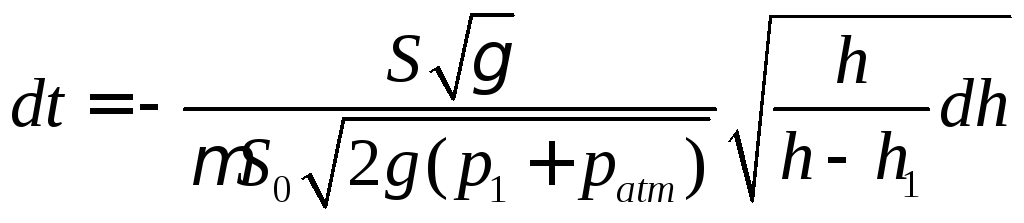
where

The required time t is found after integrating from h = h₀ to h = h₁.