14. Rate of discharge. Equation of continuity
The rate of discharge (commonly shortened to "discharge" or "flow") is defined as the quantity of fluid flowing per unit time across any section of a stream. It may be expressed in units of volume, weight or mass: volume rate of discharge Q, weight rate of discharge G and mass rate of discharge M.
The cross-sectional area of an elementary stream tube is infinitely small throughout its length, therefore the velocity v cau be assumed to be uniform at all the points of each section. Hence, the volume rate of discharge through an elementary stream tube is
(4.1)
where dS = area of the cross-section; the weight rate of discharge is
(4.2)
and the mass rate of discharge is
(4.3)
In a finite stream the velocity will generally vary across a section; the rate of discharge is therefore computed as the sum of the elementary rates of discharge of the stream tubes, i. e.,
(4.4)
Commonly the mean velocity across the section is considered:
(4.5)
whence
(4.5`)
No fluid crosses the wall of a stream tube. Hence, from the law of conservation of matter the rate of discharge of an incompressi:blo liquid in steady flow must be the same through all sections of .an elementary stream tube (Fig. 24), i. e.,
(along a stream tube)
(4.6)
This
is the equation
of continuity for
an elementary stream tube.
Introducing the mean velocity instead of the actual velocity for a finite stream contained in impermeable walls, we obtain:
(along a stream). (4.7)
Equation (4.7) shows that for an incompressible liquid the mean velocity varies inversely as the cross-sectional area of tfce stream:
(4.7`)
The equation of continuity is thus a special case of the law of conservation of matter.
15. Bernoulli's equation for a stream tube of an ideal liquid
We shall consider the steady flow of an ideal liquid subjected to a single body force, that of gravity, and develop the basic equation which gives the relation between pressure and velocity.
Consider a stream tube and in it a liquid volume of arbitrary length between sections 1 and 2 (Fig. 25). The area of section 1 is dSv the velocity through it is v1 the pressure is p1, and the elevation of the centre of gravity of the section above an arbitrary datum level is. z1. The respective quantities for section 2 are dS2, v2, p2 and z2.
In
a differential time interval dt
the
external forces move the liquid
volume to configuration 1'-2'. To the volume can be applied the
theorem of mechanics according to which the work done by external
forces on a body is equal to the change in the kinetic energy of
the body. In our case these f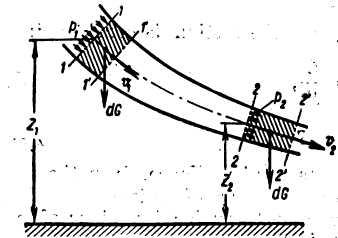
orces
are the normal pressure forceson
the sides of the stream tube and gravity.
Let us calculate the work done by the pressure forces and gravity and the change in the kinetic energy of the body of fluid in the time di.
The work done by the pressure forces on section 1 is«positive, as they are acting in the direction of the displacement, and it is equal to the product of the force p1dS1 and the path v1dt:
Fig.25. Notation for developing
Bernulli`s equation for a stream tube
The work done by the pressure forces on section 2 is negative as they are acting against the displacement, and it is equal to,
The pressure forces acting on the side walls of the stream tube do no work as they are normal to the walls and, therefore, normal to the displncerpent.
Thus, the work done by the pressure forces is
(4.8)
The work done by the gravity force, is equal to the change in the potential, or position, energy of the liquid volume. Subtracting the potential energy of volume 1'-2' from that of volume 1-2, we obtain, as the potential energy of volume 1'-2' cancels out, the difference between the potential energies of portions 1-1' and 2-2' of thle stream tube. From the continuity equation (4.6) the volumes and the weights of these portions are equal, i. e.,
(4.9)
Hence, the work done by gravity is found as the product of the change in elevation and the weight dG :
(4.10)
To determine the change in the kinetic energy of the liquid volume in the time dt, the kinetic energy of volume 1-2 must be subtracted from the kinetic energy of volume 1'-2'. The energy of the intermediate volume 1'-2' cancels out, leaving the difference between the kinetic energies of the volumes 2-2' and 1-1' the weight of both being dG. Thus, the change in the kinetic energy is equal to
(4.11)
Adding the work done by the pressure forces (4.6) and the work done by gravity (4.10) and equating the sum to the change in kinetic energy (4.11), we obtain
Dividing through by the weight dG, for which we have the two expressions (4.9), and cancelling out, we obtain
Transposing the terms referring to the first section to the left-hand side of the equation and those referring to the second section to the right-hand side, we obtain:
(4.12)
This is Bernoulli's equation for an ideal liquid. It was developed by Daniel Bernoulli in 1738.
The terms in Eq. (4.12) represent linear quantities; they are called:
z = elevation head, or potential head, or geodetic head;
= pressure head, or static head;
=
velocity head.
The sum
is called the total head.
Equation (4.12) is written for two arbitrary cross-sections of a stream tube and it expresses the equality of the total head H at the sections. As the sections were chosen arbitrarily, it follows that the total head is the same at any other section of the same stream tube, i. e.,
(along a stream tube).
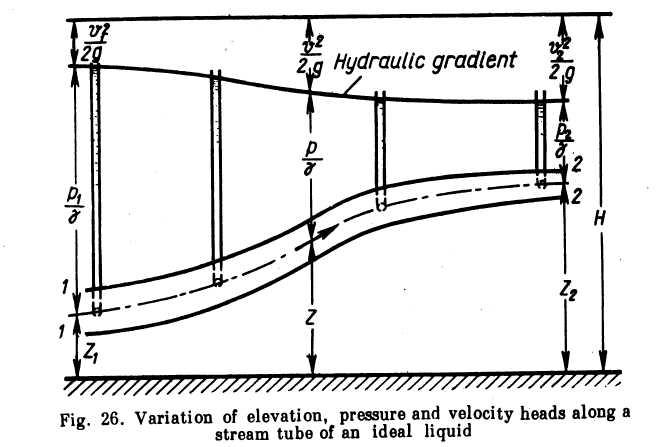
Thus, the sum of the elevation, pressure and velocity heads of an ideal liquid is constant along a stream tube.
This is illustrated by the diagram in Fig. 26, which shows the change in the three Jieads at different points of a stream tube. The line joining the pressure heads is called the piezometric line or hydraulic gradient; it is the locus of the levels that would appear in piezometric columns mounted along the stream tube.
It follows from Bernoulli's equation and the equation of continuity that the smaller the cross-section of a stream tqbe, i.e., the narrower the stream, the faster the flow and the lower the pressure; conversely, the wider the stream the slower the flow and the higher the pressure.
Let us examine the physical, or, to be more precise, the energy, meaning of Bernoulli's equation. The specific energy of a liquid is its energy per unit weight:
Specific energy is a linear quantity, like the terms in Bernoulli's equation. In fact, the latter express the different types of energy which a liquid possesses, viz.,
z
— potential energy due
to position and gravity; the potential energy
of a liquid particle of weight
at an elevation z
is
,
whence
the specific potential energy per unit weight is
=
pressure
energy due
to the pressure existing in a moving liquid;
a particle of weight
subjected to a pressure p
rises
to a height
, thereby acquiring a potential energy equal to
; divided
by
this
gives the specific pressure energy
;
- total
potential energy of
a liquid;
kinetic,
or
velocity, energy
of
a liquid;
the
specific kinetic energy of a particle
referred to unit weight is
- total
energy of a flowing liquid.
T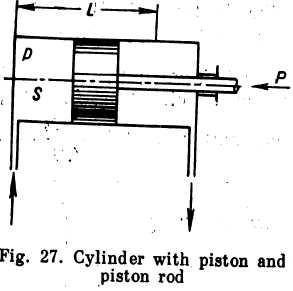
he
total energy of an ideal liquid
is constant along a streamline. Bernoulli
's equation, therefore, expresses
the law of conservation of
mechanical energy in an ideal liquid.
Thus, in fluids mechanical energy may be present in the three forms of position, pressure and kinetic energy. The first and third are characteristic of both solids and fluids; pressure energy, however, is characteristic of fluids only. In an ideal liquid one type of energy may change into another,
but the total energy, as demonstrated by Bernoulli's equation, is constant.
Energy is easily converted into mechanical work. The simplest device for this is a cylinder with piston (Fig. 27). Let us show that in the course of this conversion the work done by every unit weight of a liquid is numerically equal to the pressure head.
If the movable piston area is S, the stroke is X, the gauge pressure of the,fluid supplied into the left-hand portion of the cylinderis p, and the gauge pressure on the right-hand side is zero, then the total pressure force P, which is equal to the resistance overcome in the displacement of the piston from its extreme left to extreme right position, will be . :
P=pS,
and the work done by this force is
E=pSL;
The weight of the fluid supplied into the cylinder to do the required work is
G=SLy.
The work done per unit weight is
Bernoulli's equation is often written in another form. Multiplying Eq. (4.12) through by γ we obtain
(4.13)
All the terms now have the dimension of pressure (kg/m2), and they are called: :
zy = weight pressure;
p = static pressure, or pressure intensity, or simply pressure;
—
dynamic pressure *.
Bernoulli's equation for an ideal stream tube can also be obtained by integrating the differential equations of motion for an ideal fluid (see Appendix).