37. Flow through tubes and nozzles

A tube is a short unrounded pipe whose length is only several di­ameters [l = (2-6)d] (Fig. 88a). An orifice in a thick wall is actually a tube (Fig. 88b).

Two flow regimes are observed in efflux of a liquid through tubes with unrounded edges into a gas. The first regime is shown schemati­cally in Fig. 88a and b. On entering the tube the jet converges and forms a vena contracta in about the same way, and for the same rea­son, as in the case of a free jet through an orifice in a thin wall. Then

the jet expands and issues from the tube in a stream of the same diameter as the pipe. Between the vena contracta and tube walls a zone of violently eddying liquid is formed. As the jet has the same diameter as the aperture, ε = 1 and, consequently, μ = φ. For low-viscous liquids the mean values of the coefficients are

The rate of discharge through a circular tube running full (first regime) is greater than through an orifice in a thin wall; the veloci­ty, on the other hand, is less owing to greater friction.

Consider a jet of liquid issuing under pressure p₀ into a gas having pressure p₂ (say, into the combustion chamber of a liquid-propel-lant rocket motor). The rated head for unsuppressed contraction is

As the pressure in the jet at the tube outlet is p₂, at the vena con­tracta inside the tube, where the velocity is greater, the pressure p_x is lower than p₂. Furthermore, the higher the head under which the jet is issuing, and consequently the greater the rate of discharge, the less the absolute pressure in the vena contracta. The difference p₂ — p₁ varies as the head H. This is demonstrated by Bernoulli's equation written between sections 1-1 and 2-2 (Fig. 88a) in the form

The last term is the loss of head due to jet expansion. This is com­pletely analogous to an abrupt expansion, hence the loss of head due to expansion is given by Eq. (8.1). The vena contracta is determined by the same coefficient of contraction as in flow through an orifice. Therefore, from the continuity equation,

Using this formula to eliminate v_x from the foregoing Bernoulli equation and writing the velocity v₂ in terms of the velocity coef­ficient of the tube, we obtain the pressure drop insidethe tube:

(9.13)

Substitution of the values cp = 0.82 and e = 0.64 into this expres­sion yields

(9.13`)

At some critical head H_cr the absolute pressure at section 1-1 in the tube becomes zero and

But at H > H_cr this would mean a negative pressure p_x which is practically impossible in liquids; it follows then that at H > H_cr the first flow regime (tube running full) is impossible. This is confirmed experimentally, and at the flow regime changes suddenly. The jet springs clear of the walls of the tube and issues from it as shown in Fig. 88c.

This regime is identical to efflux through an orifice in a thin wall and it is characterised by the same jet coefficients. Thus, in a change­over from the first flow regime to the second the velocity increases and the rate of discharge, owing to jet contraction, decreases.

For the case of a jet of water into the atmosphere running clear

A submerged jet through a tube cannot run clear and the first regime persists at H>H_cr. With the head H increasing, however, the discharge coefficient drops and as a result of cavitation inside the tube the loss coefficient increases.

It follows, thus, that circular tubes possess some appreciable shortcomings: in the first regime (running full) resist­ance is great and the coefficient of dis­charge is small; in the second regime (running clear) the coefficient of discharge is even less. Furthermore, the flow regime through cylindrical tubes is unstable.

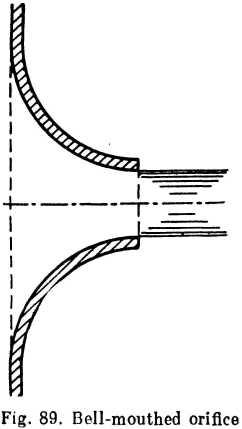
For these reasons cylindrical tubes are not favoured and, in fact, they are almost never specially provided for (with the exception of some liquid-propellant rocket motors). In engineering practice, however, tubes are frequent as bores in thick walls. Their performance can be improved substantially by rounding the inlet edge (broken lines in Fig. 88b). The greater the curve the higher the coefficient of discharge and the lower the loss coefficient. In the limit, when the radius of curvature equals the thickness of the wall, the circular tube becomes a bell-mouthed orifice (Fig. 89).

A bell-mouthed orifice is a widely used type of mouthpiece with a coefficient of discharge approaching unity, low losses, no vena con-tracta, a stable flow regime and a firm jet.

The loss coefficient is about the same as for a gradual contraction

the lower values of ζ corresponding to high Reynolds numbers and vice versa.

Correspondingly,

μ =φ = 0.99-0.96.

A diffuser mouthpiece (Fig. 90) is a diverging taper pipe affixed to a bell-mouthed orifice. Addition of a tail-pipe leads to lower pressure at the throat of the tube and, consequently, higher velocity and rate of discharge. The discharge of a bell-mouthed orifice can be increased by as much as 2.5 times by the addition of a diverging mouthpiece.

Such mouthpieces are used when the discharge for a given head must be as high as possible through a small orifice. Application, however, is limited to low heads (H = 1-4 m) as otherwise cavitation

develops in the throat, with a resulting increase in resistance and reduction of rate of discharge.

The diagram in Fig. 91 shows how the coefficient of discharge of a diverging mouthpiece is affected by the head increasing due to cav­itation at the throat. The discharge coefficient is referred to the cross-sectional area of the throat, i. e.,

The curve was obtained in tests with a cone having an optimum angle and rate of divergence ensuring the highest coefficient of discharge.

Example. In some liquid-propellant rocket motors the fuel components are supplied into the combustion chambers through so-called spray injectors which are simple boreholes. Determine the required number of oxidiser injectors for the motor of a Schmetterling rocket if G = 1.6 kg/sec, pressure drop in injec­tor Δр = 6 kg/cm², pressure in the chamber p₂ = 25 kg/cm², orifice diameter d₀ =. 1.5 mm, ratio of wall thickness to orifice diameter d/d₀ = 0.5. The oxi­diser is nitric acid, specific weight y = 1,510 kg/m⁸, kinematic viscosity v = 0.02 cm²/sec.

How many injectors would be required if 6/d₀ = 2.5?

Solution, (i) Theoretical velocity of efflux:

2. Reynolds number:

2. The graph in Fig. 84 gives the coefficient of discharge as a function of Re_t: μ= 0.62.

3. Total area of all injector mouths:

sq cm

2. Number of injectors:

2. If the bore ratio were6/d_o= 2.5, the efflux would be as from an exter­nal cylindrical tube. To determine the flow regime find /±p_cr Eq. (9.13 ) gives

kg/cm²

2. As bp_cr > AP, the first flow regime (running full) will obtain and the coefficient of discharge is \i = 0.82. Consequently,