3. Forces acting on a fluid. Pressure

In hydraulics, a fluid is treated as a continuum, i. e., a continuous medium filling a portion of space completely, without having any empty spaces. Thereby the molecular structure of matter is neglected and even infinitely small fluid particles are assumed to consist of a great number of molecules.

As a fluid will always yield with time to the slightest stress, it cannot be subject to concentrated forces. Any force acting upon a fluid is distributed uniformly throughout the volume (mass) or along the surface. Accordingly, the external forces acting on any given volume of fluid may be body or surface forces.

Body forces are proportional to the mass or, for homogeneous substances, the volume of the fluid. They arise, first of all, from the force of gravity and the forces produced in a fluid at rest inside an accelerated vessel or flowing in a channel which itself is moving with an acceleration. Body forces also appear as the "effective" D'Alembert forces in developing equations of fluid motion.

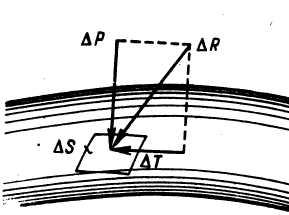
Surface forces are distributed continuously over the whole sur­face of a fluid and, in the case of uniform distribution, are propor­tional to the surface area. These forces are due to the direct action of all the surrounding fluid on a given volume or to the action of other bodies (solid, liquid or gaseous) in contact with the given fluid. In the most general case, a surface force AjR acting on a given area AS may be directed at an angle to that area and it can be resolved into a normal component AP and a tangential component AT¹ (Fig. 1). The former is called the pressure force, the latter is the friction, or shear, force.

Both body and surface forces are usually considered as unit forces, i. e.,they are referred to the corresponding units: body force to a unit mass and surface force to a unit area. As body force equals the product of mass times acceleration, a body force acting on a unit mass is numerically equal to the respective acceleration.

By hydrostatic pressure (often referred to as simply "pressure") is meant the pressure force exerted on a unit area. If the pressure force is uniform over the area, or if the mean value of the hydrostatic pressure is required, the latter is given by the formula

(1.1)

In the most general case the hydrostatic pressure at a point cor­responds to the limiting value of the ratio AP/AS as the elementary area AS shrinks to differential value at this point:

(1.2)

If pressure is measured above absolute zero, it is called absolute pressure. If it is measured either above or below atmospheric pres­sure as a base, it is called gauge pressure. Hence, absolute pressure P_ab equals atmospheric, or baro­metric, pressure p_atm plus gauge pressure p_g:

Fig. 1. Components of a surface force

A unit of pressure commonly used in engineering is the standard atmosphere:

The shear stress, or friction force, in a liquid is denoted by the Greek letter τ (tau) and, like pressure, is given by the limit

(1.3)