20. Hydrodynamic similarity

The Reynoldsnumber plays a significant part in hydraulics, as well as in aerodynamics, as an important criterion of the similarity of fluid flow. When incompressible liquids are considered similarity must be geometric, kinematic and dynamic.

Geometric similarity, it will be recalled from the course of geome­try, means proportionality of corresponding dimensions and equality of corresponding angles. In hydraulics geometric similarity is inter­preted to mean similarity of the surfaces constraining fluid flow, i. e_M similarity of channels and their relative positions (Fig. 40).

* This consideration is of practical importance in the aerodynamics of air-foils (laiminar-flow wings).

Kinematic similarity implies similarity of streamlines and propor­tionality of corresponding velocities. Obviously, kinematic simi­larity of flow requires geometric similarity of the channels.

Dynamic similarity implies proportionality of the forces acting on the corresponding elements of kinematically similar streams and equality of the direction angles of those forces.

Fluid flow is usually subjected to a variety of forces, such as pres­sure, viscosity (friction) and gravity. For complete hydrodynamic similarity, proportionality of all these different forces must be ob­served.

For example, the proportionality of the pressure forces P and the friction forces F acting on the corresponding volumes in streams I and II (Fig. 40) can be written down in the form

In actual investigations it is usually very difficult to achieve com­plete hydrodynamic similarity. Experimenters commonly deal with partial (incomplete) similarity, in which only the main forces are proportional. For flow under pressure in closed conduits (through pipes, hydraulic machines, etc.) these main forces, as calculations show, are pressure, friction and their resultants. In similar streams the resultant forces are proportional to the product of the dynamic pressure times the characteristic area S.

For a fluid particle of dimension AZ, force is the product of mass, times acceleration:

where к = dimensionless coefficient of proportionality depending on the shape of the particle; ds = elementary path of the particle.

Now multiply and divide the foregoing expression through by and , thereby introducing quantities characterising the flow as a whole. We have

The five dimensionless terms in the expression for &F have the same value for geometrically and kinematically similar streams and corresponding particles. Consequently, replacing the equality sign by a proportionality sign, we can write for these streams:

whence, as and, we finally obtain

(5.3)

For similar streams / and II we have

or

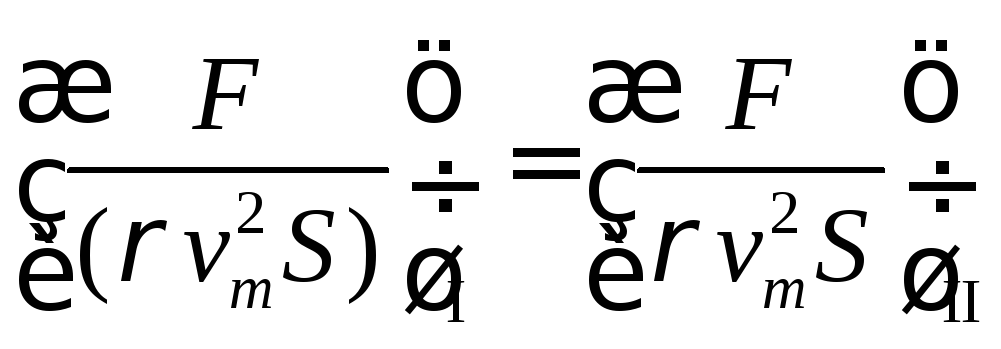
The last relation, which is the same for similar streams, is called the Newton number, denoted Ne. It should be noted that in siifiilar streams the product is also proportional to the thrust which a flow exerts (or is capable of exert­ing) on obstacles, such as walls, vanes, submerged bodies, etc. Thus, if a jet impinges normally on a flat plate of infinite area (Fig. 41) the direction of flow turns through 90°; from the well-known momen­tum equation of mechanics the impulse is

. (5.4)

This is the dynamic force acting on the plate. If the angle of ap­proach is different or if the obstacle has different shape or dimensions the proportionality factor is not unity.

Let us first consider the simplest case: motion of an ideal liquid in a horizontal plane, that is, motion not affected by viscosity or gravity.

For this case z, = z₂, and Bernoulli's theorem for cross-sections 1-1 and 2-2 in Fig. 40 takes the form:

or

For two geometrically similar streams the right-hand sides of the equation have the same value, hence the left-hand members are also equal, i.e., the pressure differences are proportional to the dyna­mic pressures:

(5.5)

Thus, for the case of an ideal incompressible fluid moving without the participation of gravity forces, geometric similarity alone ensures complete similarity of flow. The dimension less quantity representing the ratio of the pressure difference to the dynamic pressure (or of the head pressure difference to the velocity head) is called the pres­sure coefficient, or the Euler number, denoted Eu.

Let us examine the conditions that must be satisfied by the geo­metrically similar streams just considered for hydrodynamic simi­larity when shear forces are acting and, hence, there is a degradation of energy, i. e., the conditions in which the Euler numbers are the same for the two flows.

Bernoulli's equation now takes the form

or

(5.6)

The latter equation shows that Eu is the same for both streams, hence they are similar if the loss coefficients are equal (the equality of the coefficients a_t and a₂ for the corresponding cross-sections of the two streams follows from their kinematic similarity). Thus, in similar streams the coefficients £ must be the same, which means that the head losses in corresponding portions (see Fig. 40) are pro­portional to the velocity heads, i. e.,

Let us consider an important case of fluid motion: flow with fric­tion in circular pipes, for which (see Sec. 16)

In geometrically similar streams the ratio is the same, hence the similarity condition in this case is equality of the factor A, for both streams. The latter, from Eq. (4.20), is expressed in terms of tne shear stress t₀ at the wajl and tbe dynamic pressure as follows:

Hence, for the two similar streams I and II we can write

(5.7)

i. e., the shear stresses are proportional to the dynamic pressure. Taking into account Newton's law of shew, the foregoing propor­tionality can be replaced by the following;

But, as in kinematic similarity we have the proportionality

then

After the necessary transformations we obtain the condition for the similarity of fluid flow, taking viscosity into account:

or, going over to the reciprocal quantities,

This is Reynolds's law of similarity: For two geometrically similar streams of viscous fluids to be, dynamically similar, the Reynoldsnumbers for two corresponding sections of the streams must be iden­tical.

Now we see why the transition from one type of flow to another takes place at a specific Reynolds number. Furthermore, we find the physical meaning of the number for flow through pipes: it is a quantity characterising the ratio of the dynamic pressure to the shear -stress. The greater the velocity and the cross-section of a flow and the less the viscosity of a fluid, the larger the Reynolds number. For an ideal fluid Re is infinite since the viscosity is zero.

The problem of similarity is more difficult in cases when the differ­ence in elevation heads cannot be neglected in Bernoulli's equation. In such cases yet another similarity criterion is introduced: the Froude number, which takes into account the effects of gravity on fluid flow. However, for the overwhelming majority of problems of interest to the mechanical engineer this characteristic is not essential and we shall not consider it.

To sum up, in similar streams the corresponding dimensionless coefficients and numbers α, ξ, λ, Eu, Ne, Re, and several others to be introduced later on, are identical. A change in the Reynolds num­ber means a change in the relation between the basic forces acting in a stream in view of which the other factors may also change to «some extent. Thus they can all be regarded as functions of Re.