2. Метод последовательных приближений

Метод последовательных приближений применяется для решения уравнений илисистем уравнений в случаях, когда искомые параметры не могут быть выражены в явном виде. В общем случае будем пред­полагать, чтоимеется некоторая функцияF(x) и необходимо найти та­кие значения аргументах, для которых

F(^) = O. (12.1)

Функция F(x) может иметь какой угодно вид, она может быть ал­гебраической или трансцендентной, единственное, что будем предпо­лагать - это ее дифференцируемость.

В общем случае функции, которыми оперируют в задачах систем­ных исследований, не имеют аналитических формул для своих корней. Поэтому приходится пользоваться приближенными методами нахожде­ния корней, которые в основном состоят из двух этапов:

1. нахождение приближенного значения корня;

2. уточнение приближенного значения до некоторой заданной сте­пениточности.

Приближенное значение корня уравнения F(x) = 0 часто бывает из­вестно из физических соображений. Если это значение неизвестно, его можно найти с помощью грубого анализа функции. В качестве рекомен­дации можно предложить следующий метод. Определяются два такие значениях, для которыхF(x) имеет противоположные знаки, т.е. опре­деляются такиеX^t иX., для которых

F(X^t) >0 и/^rC*.) <0.

Тогда между х* и х,есть по крайней мере одна точка, где F(x) = 0. В качестве исходного приближения для нахождения корняF(x) можновзять

X₀=0,5 (х* +х.).

Рассмотрим теперь процедуры, относящиеся ко второму этапу - уточнению первоначального приближения. Численный метод, в котором производится последовательное уточнение первоначального грубого приближения, называется методом итераций. Каждый шаг в таком методе называется итерацией. Если при последовательных итерациях получаются значения, которые все ближе и ближе приближаются к ис­тинному значению корня, то говорят, что метод итеративного решения сходится. Однимиз методов получения решения спомощью итератив­ных процедур является метод последовательных приближений.

Метод последовательных приближений. Сформулируем поста­новку задачи. Имеется система уравнений вида (12.1). Необходимо определить вектор параметровX = (х,,X₂,..., x_t), при котором функция

1. достигает максимума.

Вначале рассмотрим применение метода последовательных прибли­жений для случая, когда требуется определить один параметр. Преоб­разуем уравнение (12.1) к следующему виду:G(x) - х.Это преобразо­вание можно получить, прибавив к правой и левой частям уравнения

1. искомую величину х, т.е.

F(x) + x = x. (12.2)

Пусть X₀ будет исходным приближенным значением корня уравнения

2. . Тогда в качестве следующего приближения принимается значение

*1 = ^F(^xo) ^{+ x}O-

На втором шаге в качестве приближения возьмем

*2 ^{= F}(^xi)⁺

Продолжая этот процесс дальше, в качестве п-то приближения прини­маем значение

х = FCx .)+ х..

п V Л-1' П-І

Процедура повторяется до тех пор, пока не будет достигнута задан­ная точность решения уравнения. Правило остановки можно задать следующим образом: вычислительный процесс заканчивается, когда выполняется соотношение |х_п- х_п,1 <е, гдеє - заданная точность вы­числения.

Представляет интерес рассмотрение метода последовательных при­ближений для двухпараметрического случая. Случай оценки двух па­раметров имеет прикладное значение в статистических задачах, когда исследуемые процессы описываются законом распределения с неизве­стными параметрами. Для определения параметров приходится решать, например, уравнение правдоподобия. Часто систему уравнений макси­мального правдоподобия трудно решить в явном виде. Даже для экс­поненциальных семейств система уравнений правдоподобия может быть нелинейна и трудна для решения, как это происходит при оценке параметров распределения Вейбулла. Двухпараметрические распреде­ления, например нормальное, Вейбулла, гамма-распределение, находят широкое применение в теории надежности.

При оценивании двух параметров закона распределения необходи­мо решать систему

(¹²-3)

Jx₁=FCx₁,X₂)+X₁;[ X₂ = F(x,,x₂) + x₂.

Задавая вектор начального приближения (х°,х°), находим первые приближенные оценки:

^х\ -F(X₁⁰JX₂)+ X₁⁰;

X₂ ⁼F(x°,x₂)+ х₂.

Повторяем эту процедуру до тех пор, пока разность (|х"- хГ‘|,|х₂"-х₂"‘|)не попадает вє-окрестность. Иными словами, дол­жны совместно выполняться соотношения:

|х,"-X₁"-¹! <8,

|х₂-X₂⁴1 <8 .

Значения (х",х₂)принимаются за искомую оценку вектора вычис­ляемых параметров.

Усовершенствованный метод последовательных приближе­ний. Этот метод разрабатывался в целях обеспечения более быстрой сходимости оценок. Более быстрая сходимость по сравнению с обыч­ным методом последовательных приближений достигается за счет того, что при каждой итерации делается большая поправка к очередному значению параметра х, Иначе говоря, вместо того, чтобы полагать

х = F(x ,)+ х.

п ^n-I' Л-1

применяют следующую формулу:

х_п= a F(X_{n l}) + х_п_,,где а>1.

В [8] доказано, что наилучшая сходимость достигается в случае, когда параметр а вычисляется следующим образом:

^a_l-(F(^) + ^’

где х_п<%<а,а-корень уравнения(12.1).

Значение ^ остается неизвестным, но для вычисления производной используется следующее приближение:

Формула итеративного метода приобретает в этом случае следующий вид:

0. F (x_n-d⁺x_n-v

і ^F(x_n__l )-F(x„_₂)

^Лл-1 ^лп-2

Метод Ньютона-Рафсона. Метод основан на разложении функ­ции F(x) в окрестностиа

F(x) = F(X₁)+ (a-X₁) F'(X₁)-O.

Произведем элементарные преобразования в данном уравнении, полу­чим

F(X)

а = х-

F'(x)

Заменим искомый параметр его первым приближением, получим

_{у = у} _ F(X₀)

' ° F'(x₀) ‘

Далее организуем итеративный процесс

F(X_hl)

F'(x_hl)

Если начальное приближение х₀выбрано близко к корню уравнения

1. и если производная F'(x) для/= 1,2,...не равна нулю, то последо­вательность, порожденная соотношением(12.3) сходится ка.

3. Численное интегрирование

Задачи, в которых требуется вычислить интегралы, возникают на разных этапах решения задач системного анализа. Иногда удается найти аналитическую формулу, т.е. выразить неопределенный интеграл в виде комбинаций алгебраических и трансцендентных функций, после чего остается вычислить значение определенного интеграла, подставив в формулу пределы интегрирования.

В большинстве случаев не удается найти никакой аналитической формулы или же она получается настолько сложной, что вычислять интеграл с ее помощью труднее, чем другими способами. В таких си­туациях приходится применять различные методы численного интегри-

379

рования, которые основаны на том, что интеграл представляется в виде предела суммы площадей. Далее вычисляют эту сумму с достаточно высокой степеньюточности.

Рассмотрим постановку задачи. Пусть необходимо вычислить оп­ределенный интеграл

Ь

1. =jf(x)dx

а

при условии, чтоаиЪконечныи/(х)является непрерывной функцией

10. во всем интервале а<х<Ь.Представляют интерес также те случаи, когда один или оба предела интегрирования бесконечны, либо когда подынтегральная функция имеет особенности внутри интервала интег­рирования или на его концах.

Общий подход к решению задач численного интегрирования будет следующим. Определенный интеграл /представляет собойплотят^ог­раниченную кривой/(лг), осьюX и прямымиX = а их = Ь.Задача зак­лючается в вычислении интеграла. При этом интервал интегрирования разбивается на множество более мелких подынтервалов, приближенно вычисляется площадь каждой полоски, получающейся при таком раз­биении. Далее площади полосок суммируются.

Существует множество методов вычисления определенных интег­ралов, основанных на таком разбиении и последующем суммировании. Рассмотрим некоторые из них.

^ґх -х ^{л Л}/+1 ^л

Метод прямоугольников. Пусть интервал [а, Ь\разбит на мно­жество подынтервалов [х., х.₊₁). Будем считать, что на рассматривае­мом подынтервале интегрируемая функция почти константа:f(x) ~const. Тогда для данного подынтервала можно положить:I. ~(х -х)/(Q, гдеС, -произвольная точка на рассматриваемом подынтервале. Если в качестве такой точки взять среднюю точку подынтервала, получим формулу

/,-(x,_+I -X_i)/

Далее, производя суммирование по всем подынтервалам, получим фор­мулу интегрирования по методу прямоугольников

(12.4)

где п- количество подынтервалов на отрезке интегрирования.

Метод трапеций. В отличие от метода прямоугольников, где пред­полагалось, что интегрируемая функция на каждом подынтервале близ­ка к константе, в методе трапеций принимается допущение, что функ­ция на каждом подынтервале может быть приближена линейной функ­цией. При таком предположении интеграл заменяется площадью тра­пеции с высотой (х.₊₁-х.)и основаниями/ (х.₊₁) и /(х). В результате получим формулу трапеций

/"£(^м-^і)^/(ЛС,+і)₂^+/—- (12.5)

1=0 ^

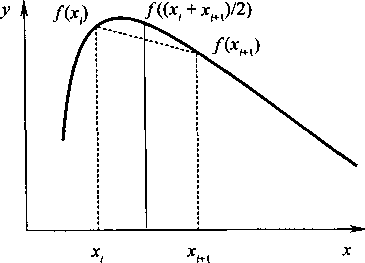
На рис. 12.1 приведена иллюстрация рассмотренных методов ин­тегрирования путем замены определенного интеграла конечной суммой, а именно показано увеличенное представление элемента площади, ограни­ченной функцией/(jc), осьюхи прямымиX = X. их = х._+гПунктирной линией выделена трапеция, которой заменяется площадь под кривой ин­тегрирования. В центре отрезка тонкой прямой линией отмечена высо­та прямоугольника, которая используется в качестве сомножителя в методе прямоугольников.

Ошибка интегрирования методом трапеций. При интегриро­вании с использованием формулы (12.5) возникает ошибка, равная сум­ме площадей между кривойу= f(x) и хордами, соединяющими точкиу.=/(jc )иу= /(х._+|). Оценим ошибку, разлагая функциюу = f (х)в ряд Тейлора в точкахjc. иX₁ .Это разложение позволит получить урав­нение исходной кривой в виде, удобном для сравнения точного значе­ния интеграла с приближенным, вычисленным по формуле(12.5).

Рассмотрим разложение функции у= f(x) в ряд Тейлора в окрест­ности точкиjc = Jt, Предположим, что интегрируемая функция имеет

Рис. 12.1. Иллюстрация численного интегрирования методом трапеций

столько производных,сколько может потребоваться.

/(*) =/(*,) + (*- X_i)/'(*) +⁾ /'(JC₁)+■■■■(12.6)

Аналогично разложим данную функцию в ряд в окрестности точки дс,получим

/(*)= f(x_M) + (х-X_m)f\x_M)+^(х *‘^чі) /'(дс_і+,) + .... (12.7)

Обозначим длину подынтервала через А, т.е. A= дс_<+1-х.и перепишем формулу(12.7)

f(x) = /(*,.) + (*-*,.-h)f\x_M) + ^~ ^Х‘--f\x_i+,) + -. (12.8) Найдем среднее из обеих представлений(12.6) и(12.8)

₊ (£^_(/._{(і) + Г(і}^_ь(І^_!)Л_Г(^_і)+^_/.⁽_ім⁾₊_ Интегрируя/ (xr)d^c в пределах отх.додс_<+1,получаем

Это выражение представляет собой оценку значения интеграла. Оценка может быть сделана как угодно точной, потому что можно взять сколько угодно большое число членов в разложении функции в ряд Тей­лора. Правило трапеций получается, если в формуле (12.9) отбросить все члены, содержащиеh в степенях выше первой. Таким образом, ошибка при использовании метода трапеций равна

E = - ^(X~h²-W(X₁) +Пх_м))^ + ... (12.10)

Для малых h первый член гораздо больше всех остальных, поэтому ошибка именно им и определяется. Более того, в[8] показано, что за счет наличия в выражении слагаемых с производными более высокого порядка ошибка определяется следующим образом

Полную ошибку интегрирования методом трапеций можно оценить сле­дующим соотношением

_е = %Е, .-^f'WW»_h\ (12.11)

і=о 12

Усовершенствованный метод трапеций. Попытаемся найти более точное значение интеграла. Для этого произведем сравнительно простое усовершенствование метода трапеций. Рассмотрим ошибку (12.11) и преобразуем данную формулу. На основании теоремы о сред­нем значении можно написать

f'(x_b)-fXx.) = Q>-a)f^r<&,

іде a<\<b,так что

(b-a)f\\).

В данном выражении обозначим

С = ~ф-а)П\\

тогда ошибку можно записать

е = Ch².

Предположим теперь, что вторая производная от интегрируемой функции является константой, тогда и Сбудет константой.

Выберем другую величину шага разбиения отрезка интегрирования к = (Ь -а)/т,причемтФп.Тогда получим выражение для ошибки ин­тегрирования в виде

е - Ck².

Запишем далее значение интеграла, вычисленное по правилу тра­пеций с шагом h -I_h и с шагомк - 1_к.Тогда будут справедливы следу­ющие выражения

/ = I.+Ch,

2. (12.12) / = /_t + Gt². ^v '

Приравняем эти два уравнения друг другу и решим их относительно С, получим

_c=hh

k²-h²

Подставляя это выражение в (12.12), получим

^,='>⁺т- ^<1213>

Вычисленное таким образом значение интеграла является лучшим приближением, чем любое представление, полученное в (12.12). Если же вторая производная интегрируемой функции действительно посто­янна на интервале интегрирования[а, Ь],то ошибка в формуле(12.13) равна нулю.

Правило Симпсона. Способ интегрирования по правилу Симпсо­на наиболее широко известный и применяемый метод численного ин­тегрирования. В данном методе, так же как и в рассмотренных ранее, интегрирование производится путем разбиения общего интервала ин­тегрирования на множество более мелких отрезков. Однако в этом методе для вычисления площади над каждым из отрезков через три последовательных ординаты разбиения проводится квадратичная па­рабола. Рассмотрим процедуру получения формулы Симпсона. Пусть, как н ранее, п -количество отрезков разбиения интервала интегриро­вания;h - ширина интервала разбиения. Предположим, что числоп является четным. Пустьк -ширина интервала при другом разбиении, такая, чток = 2А. Тоща можно записать

/* =А/2(/(х₀) + 2/(х₁) + 2/(х₂) + ... + 2/(х_|_₁) + /(х_|>)) ; (12.14) h=Kf(x₀) + 2f(x₂) + ...+ 2f(x_n_₂)+f(x_n)). (12.15)

Преобразуем выражение (12.13) учитывая, чток = 2А, получим

/ = / ₊ _₇ , h~h 4(/,-7,)

• k²/h²-1 * H¹IAh¹ -I * З

Приведем подобные члены

_z_4 I_k-I_h 3 ’

Подставим данное выражение формулы (12.14) и(12.15), окончательно получим

Л=(/(*о) + 4/(*і) + 2/(дг₂) + 4/(х,) + 2/(х₄)+...+ ч4/(х„_₂) + 2/(х„.₁) + /(х„))А/3.

Данная формула называется формулой Симпсона. Ошибка при интег­рировании с помощью формулы Симпсона равна

Как видно из данного выражения ошибка пропорциональна значе­нию А⁴,в то время как для метода трапеций она была пропорциональнаА².Это означает, что формула Симпсона соответствует ряду Тейлора с точностью до членов третьего порядка, а метод трапеций соответствует этому рядутолько сточностьюдо членов первого порядка. Поэтому при интегрировании многочленов степени не выше третьего порядка метод Симпсона дает точные значения интеграла.

Вычисление интегралов с бесконечными пределами. Рас­смотрим еще одну важную задачу численного интегрирования — вычис­ление определенного интеграла для случая, когда один или оба предела интегрирования равны бесконечности. Таким образом, предметом рас­смотрения будет вычисление одногоиз следующих выражений

~j f(x)dx, Jf(x)dx, J f(x)dx.

Поскольку вычислительная техника не работает с такими понятия­ми как бесконечность, то задача аналитика состоит в том, чтобы за­менить бесконечность реальным числом, обеспечив приэтом прием­лемую точность вычисления. Иными словами, необходимо найти такие числаАиВ,для которых были бы справедливы выражения

J / (x)dx = J /(x)dx+e; (12.16)

ВВЕДЕНИЕ 5