6. Дискретное программирование

Постановка задачи дискретного программирования. Многие задачи системного анализа, такие как распределение ресурсов, задачи сетевого планирования и управления, календарного планирования, опи­сываются математическими моделями дискретного программирования.

Рассмотрим общую задачу максимизации.

Найти тах/(х_х,х₂,..., х_п) (10.10)

при условиях

g,(x_t, X₂,..., х_п )< 0;

(10.11)

S_m (X₁,X₂,...,х_п) < 0;

V- =J-V =Ox = 4 —.

0. ОПТ 2 ⁵ 2 опт ⁹ 3 ОПТ 2

2

Проверка показывает, что никакое округление компонент этого плана не дает допустимого решения, удовлетворяющего ограничениям этой задачи. Искомое целочисленное решение задачи X_{1 опт}= 2, X_{2 от}~2,х_3от=5.

Таким образом, для решения задачи дискретного программирова­ния (ЗДП) необходимы специальные методы. Методы решения ЗДП по принципу подхода к проблеме делят на три группы: 1) методы отсече­ния или отсекающих плоскостей; 2) метод ветвей и границ; 3) методы случайного поиска и эвристические методы.

Математические модели задач дискретного программирова­ния. По структуре математической модели задачи дискретного про­граммирования разделяют на следующие классы:

1. задачи с неделимостями;

2. экстремальные комбинаторные задачи;

3. задачи на несвязных и на невыпуклых плоскостях;

4. задачи с разрывными целевыми функциями.

Рассмотрим существо некоторых из них.

Задачи с неделимостями. Математические модели задач с неде­лимостями основаны на требовании целочисленности переменных {х}, вытекающем из физических условий практических задач.

К таким задачам относится задача об определении оптимальной структуры производственной программы, где [x_jt X₂,..., х_л} - объемы выпуска продукции.

Эта задача заключается в отыскании

шfY^cj^xj (10.13)

при

Y^aij^xj-^bi(i=\,2,...,m) (10.14)

J=і

X₁ >0,х₂ >0,...,х_п 2 0;х_; -целые при je.J. (10.15)

Если J = N = (1, 2,..., п), то задача называется полностью целочис­ленной, в противном случае, ecsmJ^N-частично целочисленной.

Задача о ранце. Одной из наиболее распространенных задач цело­численного программирования является так называемая задача о ранце.

Рассмотрим постановку данной задачи. Турист готовится к длитель­ному переходу в горах. В рюкзаке он может нести груз, масса которого не более W. Этот груз может включать в себя п видов предметов, каж­дый предмет типа j, массой оо J= 1, 2,..., п. Для каждого вида предме­та турист определяет его ценность E во время перехода. Задача зак­лючается в определении количества предметов каждого типа, которые он должен положить в рюкзак, чтобы суммарная ценность снаряжения была максимальной.

Обозначим через X_j количество предметов j-го типа в рюкзаке. Тогда математическая модель задачи такова:

(10.16)

J=і

при ограничениях

Yjb_jX J<W, X_j > 0, X_j-целое, г'= 1,2,..., т. (10.17)

J=і

Экстремальные комбинаторные задачи. В данных задачах не­обходимо найти экстремум некоторой целевой функции, заданной на конечном множестве, элементами которого служат перестановки из п

символов (объектов).

Одной из наиболее простых задач этого класса является задача о назначениях-, найти такую перестановку (p_x,p₂,...,pj из чисел 1, 2, 3,...,

п

п, при которой обеспечен mmXc,_p по всем перестановкам (р_{,р₂,...,р). Каждая такая перестановка может быть представлена точкой в п²-

мерном евклидовом пространстве или в виде матрицы X^nxn = ||х,_у1|.

Вводим переменные :

10. = 1, если г'-й механизм предназначен для /-Й работы;

X_jj = 0-в противном случае.

Очевидно, что должно выполняться условие

Y^xV ^{= 1;}I^xU ^{= 1; 1 = п;}І ^{= 1}' ^п-(¹⁰-¹⁸)

>=1 J=I

Данные ограничения означают, что один механизм может быть предназначен для выполнения только одной работы. Тогда задача бу­дет состоять в определении таких чисел {xj, при которых достигает­ся минимум функционала при ограничениях (10.18). Задача о коммивояжере. Ймеется (п + 1) город. Задана матрица

С = ||с_(:/1 расстояний между городами. Выезжая из исходного города A_ff коммивояжер должен побывать во всех остальных городах по одному разу и вернуться в город A_q. Требуется определить, в каком порядке следует объезжать города, чтобы суммарное пройденное расстояние было минимально.

Введем переменные:

X_jj= 1, если коммивояжер переезжает из населенного пункта A_lBA_j;

X_ij = 0 - в противном случае.

Математическая модель задачи имеет следующий вид:

найти

^minXX^x_iy (10.19)

1*0 J= о

при условиях

Y^xU ⁼¹’(j ^{= 1}>²’-’^п);(10.20)

1=0

J_lX_ij = 1, (і = I, 2,..., n);

(10.21)

J=о

U_i-U_j^nx_ij <n-l, (i,;' = l, 2(10.22)

где и., м_у - произвольные целые и неотрицательные числа.

Условие (10.20) означает, что коммивояжер выезжает из каждого города один раз, а условие (10.21) - что он въезжает один раз в каждый город.

Если ограничить задачу только условиями (10.20) и (10.21), она бу­дет эквивалентна задаче о назначениях, план которой не обязан быть цикличным. Иначе говоря, путь коммивояжера при этом можно пред­ставить как ряд несвязанных подциклов, в то время как его путь в дей­ствительности состоит из одного цикла.

Покажем, что для любого цикла, начинающегося в A_g, можно найти

и., удовлетворяющие условию (10.22). Пусть и. =р, если коммивояжер посещает город А. нар-м этапе. Отсюда следует, что U₁- и.< п - 1 для всех і и у, и, таким образом, условие (10.22) выполняется при X_fj = 0. При X_ij = 1 условие (10.22) выполняется как строгое равенство:

U_i-U_j +nx.j = p-(p + l) + n = n-l.

Метод ветвей и границ для задачи целочисленного програм­мирования. Рассмотрим частично целочисленную задачу ЛП: минимизировать

г = /(X) = Jc_iX_i, (10.23)

1=1

при условиях

Ja_ijX_i > Ъ_}, 0 =1, 2,..., т)•; (10.24)

1=1

0<х, (i = i,2,...,л); (10.25)

х. - целые числа. (10.26)

Процесс поиска оптимального решения начинают с решения непре­рывной задачи ЛП. Если полученный при этом оптимальный план X₀ не удовлетворяет условию (10.26), то значение целевой функции ^₀=/(X₀) дает нижнюю оценку для искомого решения, т.е. min z = ^₀.

Пусть некоторая переменная х.₀ (1< i_Q < т) не получила в плане

X₀ целочисленного решения. В целочисленном плане значение X₁₀ сле­дует либо уменьшить, по крайней мере до [х.₀], либо увеличить, по край­ней мере до [X₀]+ 1.

Если границы изменения х_ю заранее не заданы, то их можно вы­числить, решив для этого две вспомогательные задачи ЛП. Эти задачи состоят в максимизации и минимизации х_ю при условиях (10.24) и (10.25).

Теперь для каждого фиксированного целочисленного значения х_й в найденном отрезке (X_0min, X_i0max) находят minz, решая задачу ЛП с огра­ничениями (10.24), (10.25) и с дополнительным ограничениемх₍₀< к_ю.

Таким образом, все указанные выше возможности можно пред­ставить в виде некоторого дерева, в котором вершина 0 отвечает плану

X₀, а каждая из соединенных с ней вершин отвечает оптимальному плану следующей задачи: минимизировать z при условиях (10.24), (10.25) и дополнительном условии, что переменной х₀ дано значение х_ю < к_ю, где к_& - целое число. Каждой из таких вершин приписывают оценку Q^k) = q(i , к), которая равна minz при указанных выше ограничениях. Оче­видно, |₀ < £(/₀, к), для всех к.

Если оптимальные планы полученных задач удовлетворяют усло­виям целочисленности, то план с минимальной оценкой = ^(/₀, к) и будет оптимальным планом исходной задачи. В противном случае воз­никает необходимость в продолжении ветвления. При этом каждый раз для очередного ветвления выбирают вершину с наименьшей оценкой.

Любой маршрут в дереве от начальной вершины 0 до некоторой вершины определяет допустимую последовательность выбора цело­численных решений для переменных. Процесс продолжают до тех пор, пока продолжение ветвления становится невозможным.

' Каждая конечная вершина отвечает некоторому допустимому це­лочисленному плану. Вершина с минимальной оценкой дает опти­мальный план.

Рассмотрим алгоритм решения задачи целочисленного программи­рования. На первом этапе необходимо задать множество G⁽⁰⁾, опреде­ляемое условиями (10.24), (10.25). Далее формируются множества

G^^}(v = l, 2,..., p_t; к = I, 2,...), задаваемые условиями (10.24), (10.25) и дополнительным условием

X_j <[*;„] или X_j <[х_;о], (10.27)

где [X_yo] - целая часть X_yo.

^Далее осуществляется вычисление оценок. Для множества G⁽⁰⁾

оценку £(G⁽⁰⁾) определяют как £(G^<0))= /(Х₀), где X₀ - оптимальный план непрерывной задачи ЛП.

;^{(1) 7}3 •

Для множества G_v'*' оценку £(G**’) определяют аналогично:

$(с'*>) = /(х<*>),

где Х<*> - оптимальный план задачи с условиями (10.24), (10.25) и с до­полнительным условием (10.27).

Если множество Gj^lci оказывается пустым, ему приписывают оценку

^Gf¹) = CO.

На следующем этапе осуществляется нахождение планов. Если план X₀ удовлетворяет условию целочисленности (10.26), X₀-оптимальный план задачи. Если X^l_v^k) удовлетворяет условию целочисленности (10.26), он является оптимальным планом задачи с условиями (10.24), (10.25), (10.27) и некоторым планом исходной задачи (10.23) - (10.26).

Далее выполняют ветвление. Ветвление производят в том случае, когда план Xf¹ не удовлетворяет условию целочисленности (10.26).

Пусть X¹_p^kJ - одна из нецелочисленных компонент плана, где 1 < р <«,, тогда множество G**¹ разбивают на два подмножества:

^gV*¹ = ^gVJ¹U^g^ ’ ⁱⁱP^h46m

G<*> ={Х/Хє Gl^kK х_р <[дсД (10.28)

G™={х/х є Gl^kK х_р >[<_v>] + l}.(10.2?)

Укажем некоторые особенности метода ветвей и границ для задач ЦП.

1. Если все коэффициенты C_j целевой функции - целые при 1 <7 < я, и равны нулю при j > я,, то оценку J;(G<‘>) можно заменить на более

сильную оценку £¹(g*^m) = ]/(x*‘’)£, где ]а[ обозначено наименьшее целое, но не меньшее, чем а, т.е. округленное до ближайшего целого с избытком.

2. Алгоритм метода в вычислительном отношении представляет собой последовательность задач ЛП, причем конечность алгоритма следует из предполагаемой ограниченности множества G.

3. Из описания алгоритма следует, что в применении метода вет­вей и границ для полностью целочисленных и для частично цело­численных задач нет никакой разницы.

Геометрически этот метод можно интерпретировать таким обра­зом. Гипер-плоскость, определяемая целевой функцией задачи, вдавли­вается внутрь многогранника планов соответствующей задачи ЛП до встречи с ближайшей целочисленной точкой этого многогранника.

■ Пример применения метода ветвей и границ для решения задач дискретного программирования. Постановка задачи следу­ющая: минимизировать функцию min(-x, +х₂) при ограничениях

Ix_l +1 Ix₂ < 38;

X₁ +х₂ <7;

Ax_l - Sx₂ < 5;

X₁, X_i > 0; X₁, х₂ - целые числа.

—* {40 231

Нулевой шаг. Оптимальный план задачи ЛП X₀ = —,— , тоща

имеем £(G₀) = ]/(X₀)[ = ]-7[ = -7.

Поскольку план X₀ не удовлетворяет условию целочисленности, возьмем его нецелочисленную компоненту X₁ и разобьем множество

G⁽⁰⁾ на G,^(l> и G‘'>:

G,^(,) = (x/XeG°,x, <4};

Gjⁿ=IXZXeG⁰, *,>5}- Первый шаг. Решаем две задачи ЛП, заключающиеся в ми­нимизации исходной задачи по множествам G,⁰⁾ и Gj¹'.

В первом случае минимум достигается при

ҐЇЇ

Множество Gj⁰ оказывается пустым, поэтому = ■

Разбиваем g,⁽¹⁾ на G₁⁰/ и G,™, где G₁^tJ' ={Х/Хе G,°\ х₂ <2j и

, G# = {Х/Хє G,⁽¹⁾, X₂ > З}. Обозначим G"¹ = G<²>, Gg =Gf, G® =G<²>.

Второй шаг. Решаем две задачи ЛП, заключающиеся в миними­зации исходной задачи при дополнительном ограничении X₁ < 2 и х₂ > 3, тогда

-5-

= -5:

= -5;

С2)

и»

Х,^=|з1 2} и ^¹(Gf) = Xf ={₂І 3} и ^¹(Gf) =

-5—

2

Gf=O^¹(Gf) = -. Производим разветвление множества G,⁽²⁾:

G,⁽²⁾ =G®(JG

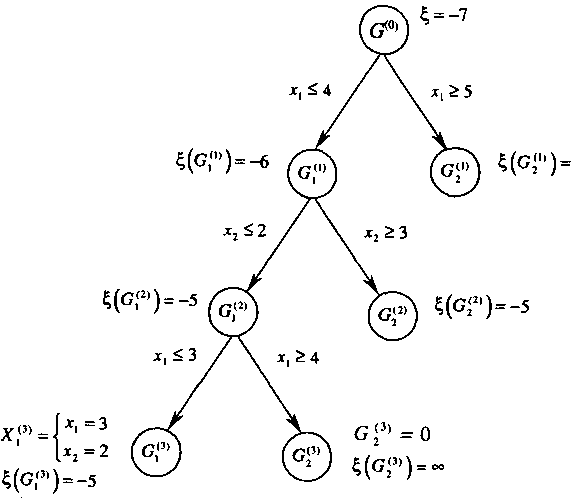
Xf = Xf =|гі, з| и S¹(Gf) = -S; G₄³ =Gf =0 и №f ) = ~. Дерево решении приведено нарис. 10.2.

Итак получен целочисленный план Xf = {3,2}, причем = min^¹ (Cf )£' (Cf )£' (Cf );^ (Cf )} = min{-5; °°; -5; ~} = -5. План Xf ={3,2} - оптимальный, так как

/(X) = -5 < min&Gf ),^(Gf ),^(Gf)}.

где Gf = {Х/Хє Gf, X₁ <3},Gf ={Х/Хє Gf, х, >4}.

Обозначим Gf = G,⁽³⁾, Gf =Gf, Gf^t = Gf, Gf =Gf.

Третий шаг. Решаем две задачи ЛП, заключающиеся в минимиза­ции исходной задачи по множествам Gf и Gf.

Находим Xf ={3,2} и §*(Gf )=]-5[=-5; Gf=O и ^'(Gf ) = -,

Рис. 10.2. Дерево решений задачи целочисленного программирования