4. Схема Эйткина

Рассм. задачу инт-ия. Ф-я задана натабл.(1) Треб. для заданного знач.вычисл. приближ. знач. ф-и, исп-я инт. мн-н. Обозн. черезинт. мн-н, постр. для ф-ипо узлам В сх. Эйткена сначала для заданного знач. арг. выб-ся ближ-й табл. узел среди всех табл-х узлов. Пусть это б. табл. узел. Этот табл.узел берется в кач-ве узла инт-ии. Соотв.табл. зн-е ф-иобозн.через. Это табл.знач. м. сч. нач. приближением к иском. зн-ю ф-и в т..Далее из ост. табл. узловвыбирается ближ. к. Это б. илиилиНайденный ближ. узел обозн.,а соотв. табл. зн-е обозн.Затем проводятся выч-я по ф-ле.(2) Здесь в числителе дроби нах. определитель кв.матрицы 2-го порядка. Опр-мый ф-ой (2) мн-нимеет 1-ую степень и для него вып-ся инт. ус-я. Б. сч. тожд-ми обоз-яиТогда ф-ла (2) м.б. переписана в виде. Выч-ое зн-еявл. 2-ым приближением к искомому зн-ию. Это зн-е получается линейной инт-ей по ф-ле (2). На след. шаге сх.Эйткена из ост. табл. узловнах. ближ. к заданному зн-июи обозн. через (берется в качестве). Новое приближение к искомому значению вычисляется по формуле (3) Перед этим предварительно должно быть вычислено , которое вычисляется по формуле, аналогичной формуле (2), в которой все индексы должны быть увеличены на 1. Легко видеть, что при этом будут выполняться условия интерполяции,.Если значенияисовпадают в пределах требуемой точности, то вычисления прекращаются. В качестве окончательного результата берется значение.В противном случае выбирается еще один узел интерполяции и проводятся вычисления по формуле 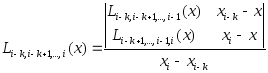(4) при i=3 и k=1, 2, 3. Формула (4) является основной вычислительной формулой схемы Эйткена.

5. Остаточный член интерполяционного многочлена Лагранжа.

Функция приближается на отрезкеинтерполяционным многочленомс узлами. Требуется оценить погрешность этого приближения, то есть, в точном равенстве

(1) нужно оценить остаточный член . Оценку будем проводить в предположении, что функциянепрерывна навместе со своими производными до-го порядка включительно. Воспользуемся вспомогательной функцией(2) В силу интерполяционных условий и вида функциифункцияв узлах интерполяцииобращается в нуль при произвольных значениях константы. Возьмем на отрезкепроизвольную точку, отличную от узлов интерполяции, и зафиксируем ее. Выберем константутак, чтобы вып-сь равенство.

Для остаточного члена, таким образом, получаем представление(3) Теперь учтем, что функцияобращается в нуль нав-ух точках:и. Эти точки делят отрезокнаотрезок, каждый из которых не имеет с другими общих внутренних точек и на концах каждого из этих отрезковобращается в нуль. По теореме Ролля внутри каждого из этих отрезков производнаяобращается в нуль по крайней мере в одной точке. Итак, из существования на-ух различных точек, в которых, следует существование-й различной точки на, где. Повторяя аналогичные рассуждения ещераз, придем к существованию напо крайней мере одной точки, для которой. Выполним дифференцирование равенства (2) и положим

: .

Отсюда получаем .

Подставляя найденное выражение для константы в равенство (3), имеем. (4)

Очевидно, значение зависит от.

Из выражения (4) для остаточного члена интерполяционного многочлена Лагранжа получаем искомую оценку

, (5) где .