
- •1.Источники и классификация погрешностей. Неустранимая и вычислительная погрешность.
- •2. Постановка задачи интерполирования. Существование и единственность обобщенного интерполяционного многочлена.
- •3. Интерполяционный многочлен Лагранжа.
- •4. Схема Эйткина
- •5. Остаточный член интерполяционного многочлена Лагранжа.
- •6. Минимиз. Оценки остаточного члена интерпол. Мн-на.
- •7. Разделенные разности и интерполяционная формула Ньютона с разделенными разностями.
- •8. Конечные разности и интерполяционные формулы Ньютона с конечными разностями.
- •9. Составление таблиц.
- •10. Сходимость интерполяционного процесса
- •11.Общая задача интерполирования алгебраическими многочленами. Интерполяционный многочлен Эрмита с узлами кратности 2.
- •13 . Оптимизация шага при численном диф-нии
- •14. Интерполяционные квадратурные формулы
- •15. Квадратурные формулы Ньютона-Котеса
- •16. Простейшие квадрат ф-лы н-Кот. И оценка их погрешности.
- •17. Составные квадратурные формулы средних прямоугольников, трапеций, парабол и оценка их погрешности
- •18. Квадратурные формулы Гаусса
- •20. Метод наименьших квадратов.
- •22.Обобщённые мног-ны наилучших среднеквадратических приближений.
- •24. Многочлены наилучших равномерных приближений. Примеры.
- •25. Наилучшие приближения в линейном нормированном пространстве.
- •26. Интерполяционные сплайны.
- •27. Существование и единственность кубического сплайна.
- •28.Краткие сведения о нормах векторов и матриц.
- •29. Обусловленность линейных алгебраических систем.
- •30. Метод Гаусса решения системы линейных ур-ний.
- •31. - Разложение квадратных матриц.
- •32. Разложение симметричных матриц. Метод квадр. Корней решения лин. Алг.Систем
- •34. Принцип сжимающих отображений в метрическом пространстве.
- •35. Метод простой итерации решения лин. Алг. Систем и усл. Его сходимости.
- •36. Метод Якоби решения линейных алгебраических систем
- •37. Метод Зейделя решения лин. Алг. Систем.
- •38. Метод покоординатного спуска решения линейных алгебраических систем.
- •39. Метод скорейшего спуска решения линейных алгебраических систем
- •40. Степенной метод решения частичной проблемы собственных значений.
- •41. Метод Данилевского раскрытия характеристического уравнения
- •42. Метод вращений решения полной проблемы собственных значений.
- •43. Метод бисекции и простой итерации решения уравнений с одним неизвестным.
- •44. Методы хорд и касательных как частные случаи метода простой итерации.
- •45. Методы локализации корней алгебраического уравнения.
- •46. Метод Лобачевского решения алгебраических уравнений.
- •47. Методы простой итерации и Зейделя решения системы нелинейных уравнений.
- •48. Метод Ньютона и аналоги метода Зейделя решения системы нелинейных уравнений.
- •49. Классификация численных методов решения задачи Коши. Методы Эйлера, трапеций и к-э.
- •50. Метод Рунге-Кутта решения задачи Коши. Построение методов р-к второго порядка точности.
- •51. Оценка погрешности и сходимость одношаговых методов решения задачи Коши.
- •52. Экстраполяц. Метод Адамса решения задачи Коши.
- •53. Интерполяционный метод Адамса решения задачи Коши.
- •54. Общий вид линейных многошаговых методов решения задачи Коши.
- •55. Условие корней многошаговых методов решения задачи Коши
- •56. Сходимость многошаговых методов решения Коши.
- •57. Сеточные методы решения краевых задач для обыкновенных дифференциальных уравнений.
- •58. Сходимость сеточного метода решения краевых задач для обыкновенных диф. Уравнений.
- •59. Методы прогонки и пристрелки решения разностных схем при решении краевых задач для обыкновенных д.У.
- •60. Эквивалентность граничных и вариационных задач
- •61. Метод Ритца решения вариационных задач.
- •62. Построение системы линейных уравнений для определения значений параметров в методе Ритца.
- •63. Вариационно-разностный вариант метода Рица.
- •64. Сеточные методы решения краевой задачи для уравнения Пуассона. Фоpмулиpовка исходной диффеpенциальной краевой задачи
- •Постpоение pазностной схемы
- •65. Основные понятия теории разностных схем.
- •66. Сходимость сеточного метода
- •Фоpмулиpовка исходной дифференциальной краевой задачи
- •67.Метод матричной прогонки решения разностной схемы. Фоpмулиpовка исходной диффеpенциальной краевой задачи
- •68. Разностные схемы для одномерного параболического уравнения. Фоpмулиpовка исходной диффеpенциальной задачи
- •69. Разностные схемы решения задачи Коши для уравнения гиперболического типа.
- •70. Сеточные методы решения смешанной задачи для уравнений гиперболического типа.
- •71. Метод квадратур решения интегрального уравнения Фредгольма 2-го рода.
- •72. Решение интегрального уравнения Фредгольма 2-го рода с вырожденным ядром.
- •Решение интегр. Ур-ния с вырожденным ядром.
- •73. Решение интегрального уравнения Фредгольма 2-го рода методом вырожденного ядра.
- •Способы приближения невырожденного ядра вырожденным.
39. Метод скорейшего спуска решения линейных алгебраических систем
Этот
метод предназначен для решения систем
линейных алгеб. уравнений
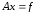 (1)
с веществ., сим-ой, положительно
определенной м-цей. Обозначим решение
системы (1) через
(1)
с веществ., сим-ой, положительно
определенной м-цей. Обозначим решение
системы (1) через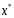 .
Из положит. опр-ти и сим-ти матрицы
следует
.
Из положит. опр-ти и сим-ти матрицы
следует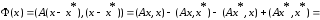
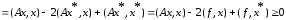 .
Отсюда видно, что минимум ф-ла
.
Отсюда видно, что минимум ф-ла
 достигается на решении
достигается на решении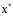 системы
(1). Т. о., решение системы (1) сводится к
минимизации ф-ла. Для минимизации ф-ла
воспользуемся градиентным методом. В
направлении градиента
системы
(1). Т. о., решение системы (1) сводится к
минимизации ф-ла. Для минимизации ф-ла
воспользуемся градиентным методом. В
направлении градиента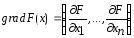 скорость
возрастания ф-ла наибольшая. В данном
случае для градиента ф-ла справедливо
рав-во
скорость
возрастания ф-ла наибольшая. В данном
случае для градиента ф-ла справедливо
рав-во
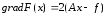 .
Действительно, проводя диф-ие, имеем
.
Действительно, проводя диф-ие, имеем

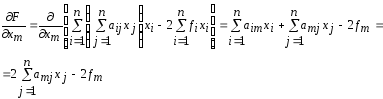 .
.
Вектор
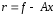 задает
направление, противоп. градиенту, то
есть направление, в котором скорость
убывания ф-ла наибольшая, если двигаться
из точки
задает
направление, противоп. градиенту, то
есть направление, в котором скорость
убывания ф-ла наибольшая, если двигаться
из точки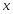 .
Пусть найдено приближение
.
Пусть найдено приближение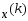 к решению. Рассмотрим процесс нахождения
очередного приближ.
к решению. Рассмотрим процесс нахождения
очередного приближ.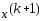 в методе скорейшего спуска. Направление
наибольшей скорости убывания функционала
в точке
в методе скорейшего спуска. Направление
наибольшей скорости убывания функционала
в точке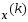 задается вектором
задается вектором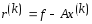 .(2)
Этот вектор наз. еще вектором невязок
системы для приближения
.(2)
Этот вектор наз. еще вектором невязок
системы для приближения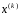 .
Точка
.
Точка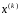 находится на поверхности уровня
находится на поверхности уровня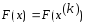 и вектор невязок
и вектор невязок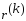 ортогонален этой поверхности уровня в
точке
ортогонален этой поверхности уровня в
точке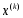 .
Будем искать минимум ф-ла на множестве
точек
.
Будем искать минимум ф-ла на множестве
точек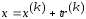 ,
где числовой параметр t0.
При этом для ф-ла имеем
,
где числовой параметр t0.
При этом для ф-ла имеем
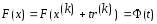 ,
то есть задача минимизации ф-ла на
направлении наибольшей скорости его
убывания сводится к нахождению минимума
функции одного переменного. Соответствующее
значение числового параметра
,
то есть задача минимизации ф-ла на
направлении наибольшей скорости его
убывания сводится к нахождению минимума
функции одного переменного. Соответствующее
значение числового параметра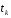 определяется из условия равенства нулю
производной
определяется из условия равенства нулю
производной
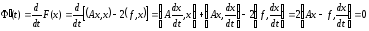 .
.
Подставляя
сюда выражение для
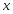 ,
получаем уравнение
,
получаем уравнение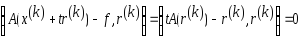 .
Отсюда
.
Отсюда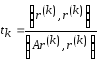 (3)
(3)
Очередное
приближение в методе скорейшего спуска
выч-ся по ф-ле
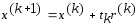 (4).
В методе скорейшего спуска нужно задать
начальное приближ.
(4).
В методе скорейшего спуска нужно задать
начальное приближ.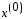 к решению системы (1) и по расчетным
формулам (2), (3), (4) вычислять очередные
приближения до получения решения с
требуемой точностью.Теорема.
Если м-ца A
вещественная,
сим-ая и
полож. определенная, то последовательные
приближения
к решению системы (1) и по расчетным
формулам (2), (3), (4) вычислять очередные
приближения до получения решения с
требуемой точностью.Теорема.
Если м-ца A
вещественная,
сим-ая и
полож. определенная, то последовательные
приближения
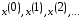 ,
построенные по методу покоорд. спуска,
сходятся к решению системы
,
построенные по методу покоорд. спуска,
сходятся к решению системы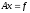 при любом начальном приближении со
скоростью геометрич. прогрессии.Доказательство.
Пусть
при любом начальном приближении со
скоростью геометрич. прогрессии.Доказательство.
Пусть
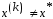 .
Тогда хотя бы одно уравнение системы
(1) не удовлетв. и по формулам (2), (3), (4)
будет найдено приближение
.
Тогда хотя бы одно уравнение системы
(1) не удовлетв. и по формулам (2), (3), (4)
будет найдено приближение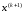 ,
для которого вып-ся нер-во
,
для которого вып-ся нер-во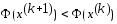 .
Обозначим через
.
Обозначим через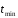 минимальное значение ф-ции
минимальное значение ф-ции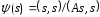 на единичной сфере
на единичной сфере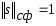 .
Так как
.
Так как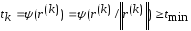 ,
то
,
то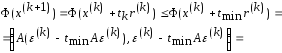
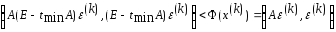 .
Далее вводится функция
.
Далее вводится функция
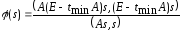 и теорема доказана.
и теорема доказана.
40. Степенной метод решения частичной проблемы собственных значений.
Пусть
собст. Знач. матр.
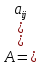 удовлю
нер-ам
удовлю
нер-ам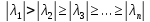 .
Будем считать также, что матрица обладает
полной системой собственных векторов.
Возьмем произв-ый вектор
.
Будем считать также, что матрица обладает
полной системой собственных векторов.
Возьмем произв-ый вектор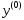 ,
разл. его по системе собст-х вект.
,
разл. его по системе собст-х вект.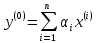 и
обр. последовательность векторов по
правилу
и
обр. последовательность векторов по
правилу
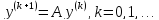 (1)
(1)
При этом получаем:
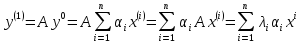
,…,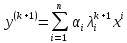 .
.
Компоненты векторов посл-ти можно представить в виде.
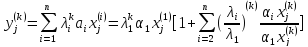 (2)
(2)
Найдем выражение для отношения компонент соседних векторов в последовательности (1)
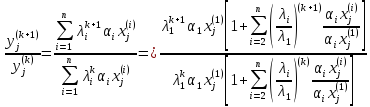
Так
как
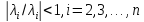 ,отсюда
имеем.
,отсюда
имеем.
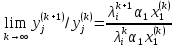 (3)
(3)
В сист.
методе построенная посл. (1) прекращается,
когда с заданной точностью для всех
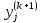 и
и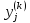 отнош.
отнош.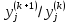 будет одинаковым, тогда
будет одинаковым, тогда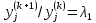 ,
а за собств. вектор можно принять
,
а за собств. вектор можно принять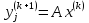 ,
где
,
где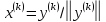 .
.
41. Метод Данилевского раскрытия характеристического уравнения
Метод Данилевского
представляет собой способ построения
невырожденного преобразования,
приводящего матрицу
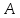 к форме Фрабениуса
к форме Фрабениуса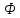 :
:

Найдем
характеристический многочлен
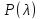 матрицы
матрицы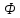 .
Имеем:
.
Имеем:


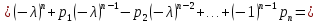
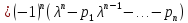
Таким образом,
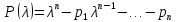 ,т.е.
в первой строке матрицы
,т.е.
в первой строке матрицы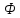 стоят коэффициенты характ-ого многочлена.
Метод Данилевского заключается в
построении посл-ти матриц
стоят коэффициенты характ-ого многочлена.
Метод Данилевского заключается в
построении посл-ти матриц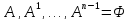 .
Рассмотрим первый шаг этого метода, в
котором строятся невырожденные
преобразования, приводящие матрицу
.
Рассмотрим первый шаг этого метода, в
котором строятся невырожденные
преобразования, приводящие матрицу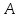
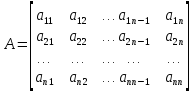
к матрице
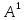 .
Будем считать, что все операции корректны.
На первом этапе поделим
.
Будем считать, что все операции корректны.
На первом этапе поделим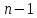 столбец матрицы
столбец матрицы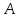 на элемент
на элемент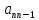 ,
т.е. проводим вычисления по формуле:
,
т.е. проводим вычисления по формуле: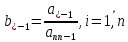 (1)
(1)
Полученный
столбец умножим на элемент
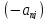 и прибавим к
и прибавим к
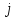 столбец для
столбец для
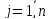 ,
,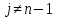 .
Т.е. вычисления проводим по формулам:
.
Т.е. вычисления проводим по формулам:
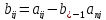 ,
,
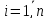 ,
,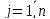 ,
, (2)
(2)
В
результате указанных преобразований
по формулам (1),(2) получим матрицу
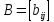 .
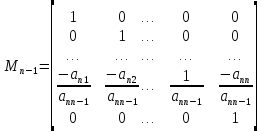
Рассмотрим матрицу
.
Рассмотрим матрицу
Формулы
(1),(2) можно записать в матрицу в виде
так:
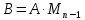 .
Так же заметим, что в результате указанных
преобразований последняя строка матрицы
.
Так же заметим, что в результате указанных
преобразований последняя строка матрицы
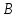 совпадает с последней строкой с матрицей
совпадает с последней строкой с матрицей
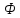 .
.
Непосредственно проверкой убеждаемся, что

Построим
матрицу
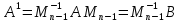 . (3)
. (3)
Здесь вычисления проводим по формулам:
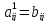 ,
,
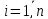 ,
,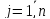 ,
,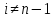 (4)
(4)
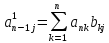 ,
,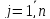 (4)
(4)
Из формул
(4) видно,что при умножении матрицы
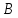 на матрицу
на матрицу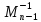 меняется
только
меняется
только
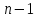 строка. Таким образом, на первом шаге
построена невырожденное преобразование
(3) такое, что последняя строка матрицы
строка. Таким образом, на первом шаге
построена невырожденное преобразование
(3) такое, что последняя строка матрицы
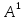 совподает с последней строкой матрицы
совподает с последней строкой матрицы
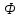 .
Переходим к построению матрицы матрицы
.
Переходим к построению матрицы матрицы
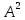 .
.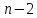 столбец этой матрицыделим
на элемент и продолжаем указанный
процесс. В результате получим матрицу
столбец этой матрицыделим
на элемент и продолжаем указанный
процесс. В результате получим матрицу
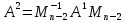 ,
у которой
,
у которой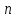 и
и
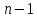 строки совпадают с матрицей
строки совпадают с матрицей
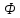 ,
и т.д. На последнем шаге будет построена
матрица
,
и т.д. На последнем шаге будет построена
матрица
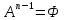 ,
т.е. будет построено преобразование
,
т.е. будет построено преобразование
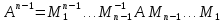 приводящее
матрицу
приводящее
матрицу
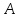 к
форме Фрабениуса.
к
форме Фрабениуса.
Выше
рассмотрено так называемый регулярный
случай, т.е. случай, когда все
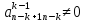 .
Имеет место два нерегулярных случая.
.
Имеет место два нерегулярных случая.
Пусть
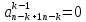 ,но
существует
,но
существует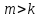 ,что
,что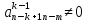 (т.е. в
(т.е. в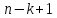 строке матрицы
строке матрицы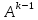 существует ненулевой элемент, располож.
левое элемента
существует ненулевой элемент, располож.
левое элемента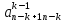 ).
Тогда в матрице
).
Тогда в матрице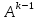 поменяем местами столбцы
поменяем местами столбцы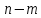 и
и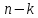 .
Рассмотрим матрицу
.
Рассмотрим матрицу

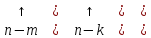
Перестановка в
матрице
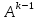 местами столбцов
местами столбцов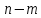 и
и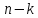 представляет собой умножение матрицы
представляет собой умножение матрицы на матрицу
на матрицу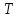 справа.
справа.
Заметим что обратной
перестановкой столбцов востанавл.
исходный вид матрицы, поэтому
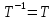 .
.
Рассмотрим матрицу
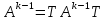 (5).
При умножении некоторой матрицы на
матрицу
(5).
При умножении некоторой матрицы на
матрицу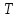 слева, у исходной матрицы меняются
строки с номерами
слева, у исходной матрицы меняются
строки с номерами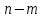 и
и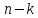 местами (но не изменяется строка
местами (но не изменяется строка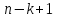 ).
).
Таким образом в
рассмотриваемой нерегулярном случае
выполн. преобразование (5), которое будет
невырожденным. После этого для матрицы
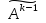 имеем регулярный случай.
имеем регулярный случай.
Пусть
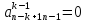 и
кроме этого
и
кроме этого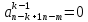
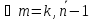 .
В этом случае матрица
.
В этом случае матрица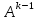 примет следующую структуру:
примет следующую структуру: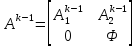
Характ. многочлен
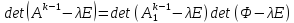 т.е. исходная задача сведена к задаче
построения преобразов. подобия,
приводящего матрицу
т.е. исходная задача сведена к задаче
построения преобразов. подобия,
приводящего матрицу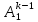 ,
к форме Фрабениуса, причем порядок этой
матрицы меньше порядка исходной матрицы.
,
к форме Фрабениуса, причем порядок этой
матрицы меньше порядка исходной матрицы.
