
- •1.Источники и классификация погрешностей. Неустранимая и вычислительная погрешность.
- •2. Постановка задачи интерполирования. Существование и единственность обобщенного интерполяционного многочлена.
- •3. Интерполяционный многочлен Лагранжа.
- •4. Схема Эйткина
- •5. Остаточный член интерполяционного многочлена Лагранжа.
- •6. Минимиз. Оценки остаточного члена интерпол. Мн-на.
- •7. Разделенные разности и интерполяционная формула Ньютона с разделенными разностями.
- •8. Конечные разности и интерполяционные формулы Ньютона с конечными разностями.
- •9. Составление таблиц.
- •10. Сходимость интерполяционного процесса
- •11.Общая задача интерполирования алгебраическими многочленами. Интерполяционный многочлен Эрмита с узлами кратности 2.
- •13 . Оптимизация шага при численном диф-нии
- •14. Интерполяционные квадратурные формулы
- •15. Квадратурные формулы Ньютона-Котеса
- •16. Простейшие квадрат ф-лы н-Кот. И оценка их погрешности.
- •17. Составные квадратурные формулы средних прямоугольников, трапеций, парабол и оценка их погрешности
- •18. Квадратурные формулы Гаусса
- •20. Метод наименьших квадратов.
- •22.Обобщённые мног-ны наилучших среднеквадратических приближений.
- •24. Многочлены наилучших равномерных приближений. Примеры.
- •25. Наилучшие приближения в линейном нормированном пространстве.
- •26. Интерполяционные сплайны.
- •27. Существование и единственность кубического сплайна.
- •28.Краткие сведения о нормах векторов и матриц.
- •29. Обусловленность линейных алгебраических систем.
- •30. Метод Гаусса решения системы линейных ур-ний.
- •31. - Разложение квадратных матриц.
- •32. Разложение симметричных матриц. Метод квадр. Корней решения лин. Алг.Систем
- •34. Принцип сжимающих отображений в метрическом пространстве.
- •35. Метод простой итерации решения лин. Алг. Систем и усл. Его сходимости.
- •36. Метод Якоби решения линейных алгебраических систем
- •37. Метод Зейделя решения лин. Алг. Систем.
- •38. Метод покоординатного спуска решения линейных алгебраических систем.
- •39. Метод скорейшего спуска решения линейных алгебраических систем
- •40. Степенной метод решения частичной проблемы собственных значений.
- •41. Метод Данилевского раскрытия характеристического уравнения
- •42. Метод вращений решения полной проблемы собственных значений.
- •43. Метод бисекции и простой итерации решения уравнений с одним неизвестным.
- •44. Методы хорд и касательных как частные случаи метода простой итерации.
- •45. Методы локализации корней алгебраического уравнения.
- •46. Метод Лобачевского решения алгебраических уравнений.
- •47. Методы простой итерации и Зейделя решения системы нелинейных уравнений.
- •48. Метод Ньютона и аналоги метода Зейделя решения системы нелинейных уравнений.
- •49. Классификация численных методов решения задачи Коши. Методы Эйлера, трапеций и к-э.
- •50. Метод Рунге-Кутта решения задачи Коши. Построение методов р-к второго порядка точности.
- •51. Оценка погрешности и сходимость одношаговых методов решения задачи Коши.
- •52. Экстраполяц. Метод Адамса решения задачи Коши.
- •53. Интерполяционный метод Адамса решения задачи Коши.
- •54. Общий вид линейных многошаговых методов решения задачи Коши.
- •55. Условие корней многошаговых методов решения задачи Коши
- •56. Сходимость многошаговых методов решения Коши.
- •57. Сеточные методы решения краевых задач для обыкновенных дифференциальных уравнений.
- •58. Сходимость сеточного метода решения краевых задач для обыкновенных диф. Уравнений.
- •59. Методы прогонки и пристрелки решения разностных схем при решении краевых задач для обыкновенных д.У.
- •60. Эквивалентность граничных и вариационных задач
- •61. Метод Ритца решения вариационных задач.
- •62. Построение системы линейных уравнений для определения значений параметров в методе Ритца.
- •63. Вариационно-разностный вариант метода Рица.
- •64. Сеточные методы решения краевой задачи для уравнения Пуассона. Фоpмулиpовка исходной диффеpенциальной краевой задачи
- •Постpоение pазностной схемы
- •65. Основные понятия теории разностных схем.
- •66. Сходимость сеточного метода
- •Фоpмулиpовка исходной дифференциальной краевой задачи
- •67.Метод матричной прогонки решения разностной схемы. Фоpмулиpовка исходной диффеpенциальной краевой задачи
- •68. Разностные схемы для одномерного параболического уравнения. Фоpмулиpовка исходной диффеpенциальной задачи
- •69. Разностные схемы решения задачи Коши для уравнения гиперболического типа.
- •70. Сеточные методы решения смешанной задачи для уравнений гиперболического типа.
- •71. Метод квадратур решения интегрального уравнения Фредгольма 2-го рода.
- •72. Решение интегрального уравнения Фредгольма 2-го рода с вырожденным ядром.
- •Решение интегр. Ур-ния с вырожденным ядром.
- •73. Решение интегрального уравнения Фредгольма 2-го рода методом вырожденного ядра.
- •Способы приближения невырожденного ядра вырожденным.
28.Краткие сведения о нормах векторов и матриц.
Будем
обозначать пространство
векторов столбцов:
пространство
векторов столбцов:
 ,
, пространство квадратных матриц
пространство квадратных матриц .
.
Нормой вектора
 наз. Число ||x||
удвл. Условиям:
наз. Число ||x||
удвл. Условиям:
1) ||x||>=0, ||x||=0 x=0.
2) ||µx||=
|µ|*||x||,

3) ||x+y||<=
||x||+||y||,
 x,
y
x,
y .
.
Нормой матрицы B наз. Число ||B||
удвл. след. условиям:
наз. Число ||B||
удвл. след. условиям:
||B||>=0, ||B||=0 B=0
|| µB||=| µ| *||B||,
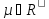
||B+C||<=||B||+||C||,

||B*C||<=||B||*||C||,

Если для матричной нормы имеют место условия 1-3, то такая норма наз. обобщённой или аддитивной. Если выполняются все 4 условия, то норма называется мультипликативной.
Интерес представляют
матричные нормы, связанные с векторной
нормой. Одна из таких связей может быть
условием согласованности, а именно,
матричная норма называется согласованной
с векторной нормой, если ||Вx||<=
||B||*||x||, ,x
,x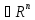 .
.
Более сильным
условием, чем условие согласованности
является условие подчинённости, т.е.
матричная норма называется подчинённой
векторной норме, если ||B||=
Очевидно, что
последнее равенство можно записать в
виде ||B||=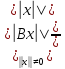 (1)
(1)
Заметим, что подчинённая норма единичной матрицы Е всегда равна 1. Действительно,
||E||= .
.
Рассмотрим важнейшие случаи векторных норм и им подчинённых матричных норм:
Норма бесконечность или кубическая норма:

Матричная
норма, ей подчин. определ. так:

Докажем,
это: имеем

Теперь
для док-ва осталось поделить полученную
оценку на
 и воспользоваться (1).
и воспользоваться (1).
Норма-единица или октандрическая норма
 .
Подчин. ей матричная норма определяется
так:
.
Подчин. ей матричная норма определяется
так:

Евклидова или сферичная норма
 =
=
Матричная
норма, ей подчин. определ. так:
 ,
где
,
где собственные
значения матрицы В*ВТ.
Докажем
это. Будем обозначать (. , .) – скалярное
произведение в
собственные
значения матрицы В*ВТ.
Докажем
это. Будем обозначать (. , .) – скалярное
произведение в
 .
Тогда,
.
Тогда, м-ца В*ВТ
является
симм. положит. определ. ,а поэтому обладает
различными положительными собственными
значениями
м-ца В*ВТ
является
симм. положит. определ. ,а поэтому обладает
различными положительными собственными
значениями
 , которые соотв. лин. нез.cобств.
, которые соотв. лин. нез.cобств.
векторы
 .
Представим векторx=
.
Представим векторx=
Тогда,
 В*ВТx,x)=(
В*ВТ
В*ВТx,x)=(
В*ВТ Т
Т
Теперь справедливость утверждения следует из формулы (1).
Матричная норма Фробениуса
 =
= Эта норма согласована с Евклидовой
векторной нормой, но не является
подчинённой.
Эта норма согласована с Евклидовой
векторной нормой, но не является
подчинённой.
29. Обусловленность линейных алгебраических систем.
Рас-м
сис-мы лин. алг. ур-й
 (1)
и
(1)
и , (2)
, (2)
которые
отличаются только правыми частями.
Будем считать, что обе системы имеют
решения: соответственно
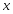 и
и при любых правых частях. Обозначим
при любых правых частях. Обозначим ,
, .
Сис-ма (1) наз-ся устойчивой по правой
части, если при любых
.
Сис-ма (1) наз-ся устойчивой по правой
части, если при любых справедлива оценка
справедлива оценка , (3)
где
, (3)
где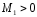 - константа, не зависящая от правых
частей
- константа, не зависящая от правых
частей .
.
Устойчивость по правой части означает, что абсолютная погрешность решения системы стремится к нулю при стремлении к нулю абсолютной погрешности правой части.
Теорема
1.
Если
 ,
то (1) устойч. по правой части.
,
то (1) устойч. по правой части.
Доказательство.
Система (1) имеет единственное решение
при любой правой части. При вычитании
(2) из (1) имеем
 ,
откуда получаем
,
откуда получаем и
и , (4)
то есть, выполняется неравенство (3) с
константой
, (4)
то есть, выполняется неравенство (3) с
константой .
Теорема доказана.
.
Теорема доказана.
Число
 наз-ся числом обусловленности м-цыA.
наз-ся числом обусловленности м-цыA.
Для
практики важной является оценка
относительной погр-ти решения. Из (1)
следует неравенство
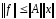 .(5)
.(5)
Перемножая (5) и (4), получим искомую оценку
 , (6).
Т. о., число обусловленности показывает,
во сколько раз относительная погр-ть
решения больше относительной погр-ти
правой части при точно заданной матрице.
Матрицы с большим числом обусловленности
наз. плохо обусловленными матрицами.
, (6).
Т. о., число обусловленности показывает,
во сколько раз относительная погр-ть
решения больше относительной погр-ти
правой части при точно заданной матрице.
Матрицы с большим числом обусловленности
наз. плохо обусловленными матрицами.
Пусть
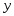 - собств. вектор матрицы А, соответствующий
наибольшему по модулю собственному
значению:
- собств. вектор матрицы А, соответствующий
наибольшему по модулю собственному
значению: .
Отсюда последовательно получаем
.
Отсюда последовательно получаем
 ,
,
 .
Поскольку
.
Поскольку ,
то
,
то .
Из полученных нер-в следует, что
.
Из полученных нер-в следует, что
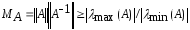 . (7)
. (7)
Из
свойства (7) для числа обусловленности
матрицы А следует свойство
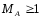 . (8)
. (8)
Отметим еще одно свойство числа обусловленности
 . (9)
. (9)
Рассмотрим
наряду с системой (1) систему
 (10)
и проведем полную оценку погрешности.
Обозначим
(10)
и проведем полную оценку погрешности.
Обозначим .
.
Лемма
1. Пусть С – квадратная матрица и
 .
Тогда существует обратная матрица
.
Тогда существует обратная матрица и выполняется оценка
и выполняется оценка . (11)
. (11)
Доказательство.
Для любого вектора
 имеем
имеем
 , (12)
где
, (12)
где
 .
След-но, однородная система
.
След-но, однородная система имеет только тривиальное решение.
Поэтому
имеет только тривиальное решение.
Поэтому и существует матрица
и существует матрица .
Возьмем произв. вектор
.
Возьмем произв. вектор и обозначим
и обозначим .
При подстановке этого выражения для
.
При подстановке этого выражения для в (12) получим
в (12) получим или
или .
Поскольку полученное нер-во выполняется
для любого ненулевого вектора
.
Поскольку полученное нер-во выполняется
для любого ненулевого вектора ,
то отсюда с учетом определения нормы
матрицы следует оценка (11). Лемма доказана.
,
то отсюда с учетом определения нормы
матрицы следует оценка (11). Лемма доказана.
Теорема
2. Пусть матрица
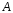 имеет обратную и выполнено условие
имеет обратную и выполнено условие . (13)
Тогда матрица
. (13)
Тогда матрица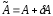 имеет обратную и имеет место оценка
имеет обратную и имеет место оценка (14)
(14)
Доказательство.
Имеем
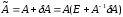 .
По условию (13) выполняется
.
По условию (13) выполняется .
Поэтому согласно лемме 1 существует
.
Поэтому согласно лемме 1 существует ,
а значит, существует и
,
а значит, существует и
 . (15)
Первое утверждение теоремы доказано.
. (15)
Первое утверждение теоремы доказано.
Из (1)
и (10) имеем
 и
и ,
откуда для искомой погрешности получаем
,
откуда для искомой погрешности получаем
 .Т.
о.,
.Т.
о.,
 и
и . (16)
. (16)
Из (15) и леммы 1 следует оценка
 . (17)
. (17)
Используя
в (16) оценку (17) и учитывая, что
 приходим к искомой оценке (14). Теорема
доказана.
приходим к искомой оценке (14). Теорема
доказана.
