1.4. Метод ортогональных проекций

Сущность метода заключается в том, что заданный геометрический объект ортогонально проецируется на две или три взаимно - перпендикулярные плоскости.

1.5. Ортогональные проекции точки.

Зададим три взаимно - перпендикулярные плоскости (рис. 3) и точку А в пространстве. П₁, П₂, П₃ - плоскости проекций: П₁ - горизонтальная; П₂ -фронтальная; П₃ - профильная. Линии пересечения плоскостей проекций - ОХ, OY, OZ - оси проекций.

Из точки А следует опустить перпендикуляры на три плоскости проекций. Точки пересечения перпендикуляров: с плоскостью П₁ - А₁ (горизонтальная проекция точки А); с плоскостью П₂ - А₂ (фронтальная проекция); с плоскостью П₃ - А₃ (профильная проекция).

Для получения плоского чертежа плоскость П₁ повернем вокруг оси ОХ вниз до совмещения с плоскостью П₂, а плоскость П₃ совмещаем с плоскостью П₂ , поворачивая ее вокруг оси OZ вправо.

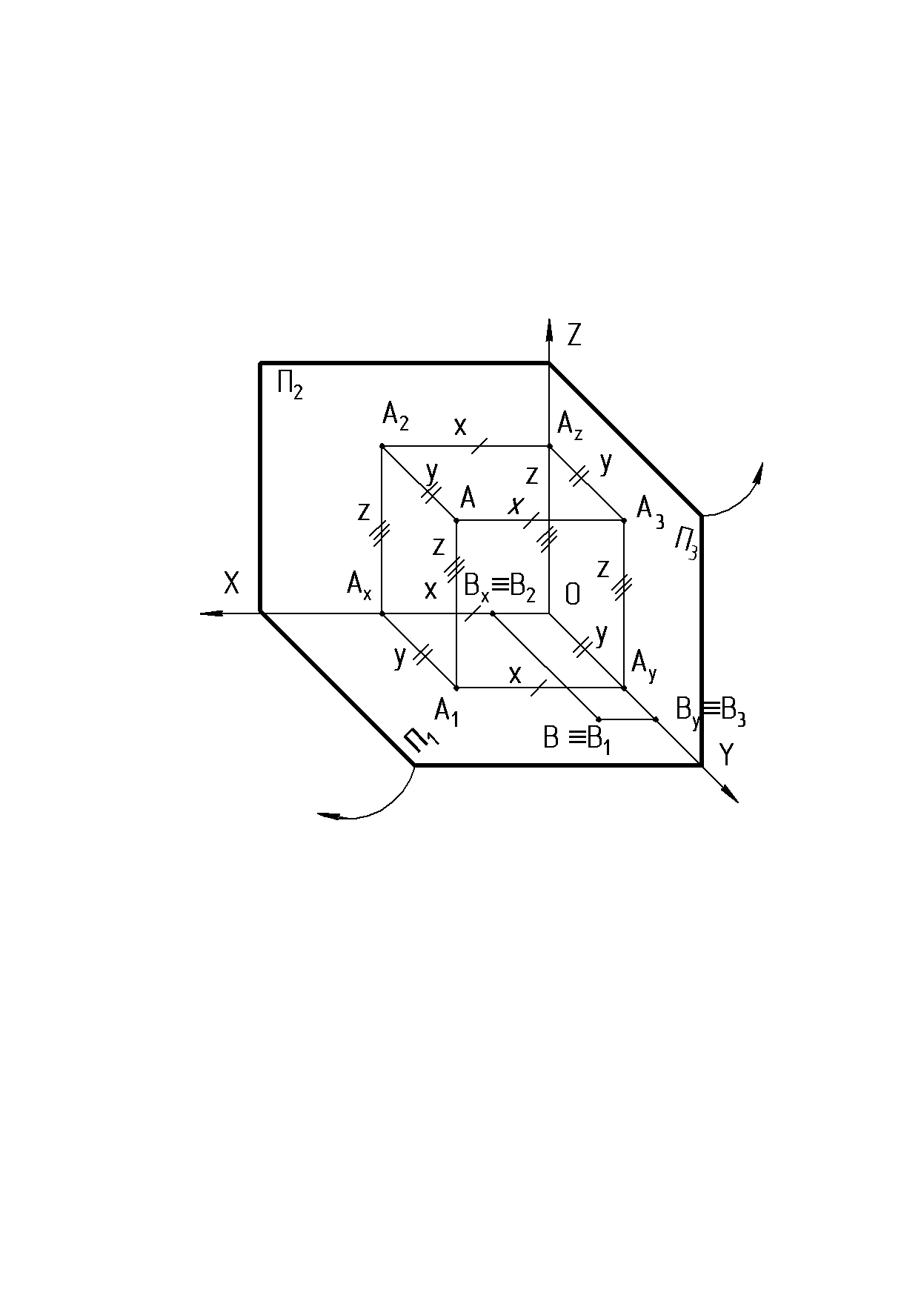
Рис. 3

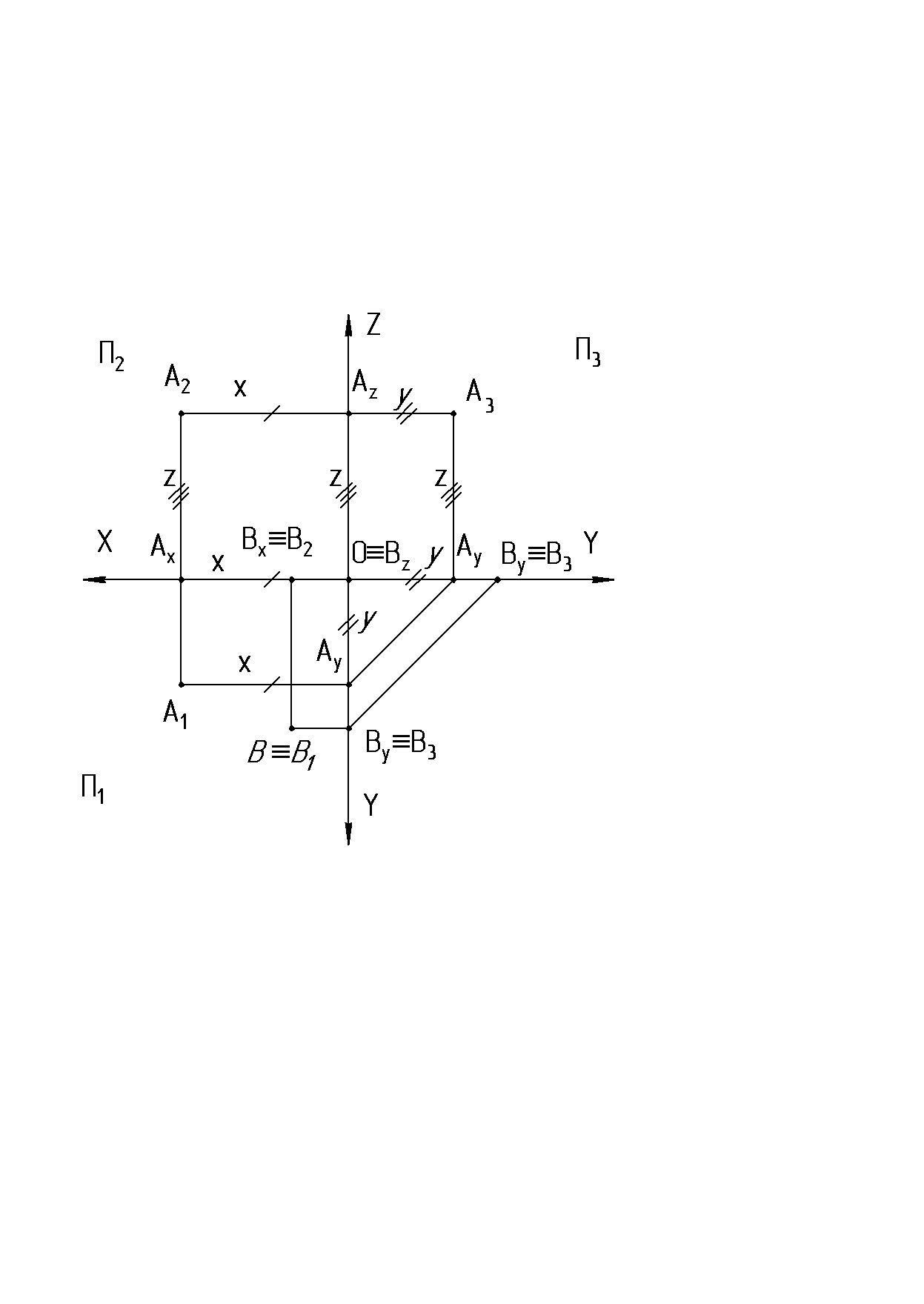
Рис. 4

Плоский чертеж, полученный в результате совмещения плоскостей П₁ и П₃ с плоскостью П₂ со всем тем, что на этих плоскостях находится, называется комплексным чертежом или «эпюром» Монжа (рис. 4). Эпюр обеспечивает точность и удобность изображений при значительной простоте построений.

Две параллельные проекции точки на взаимно – перпендикулярные плоскости лежат на прямых, перпендикулярных к соответствующей оси проекций и пересекающих эту ось в одной и той же точке. Эти линии принято называть линиями связи. Расстояния от точки до плоскости проекций называются координатами этой точки.

АА₁ = А₂А_х = ОА_z = Z (удаление точки от горизонтальной плоскости проекций)

АА₂ = А₁А_х = А_yО = Y (удаление точки от фронтальной плоскости проекций)

АА₃ = А₁А_y = ОА_x = X (удаление точки от профильной плоскости проекций)

На эпюре две любые точки, лежащие на одной линии связи, определяют ее положение в пространстве, то есть по ним можно определять координаты точек. Третья проекция строится по двум данным. Если точка лежит в плоскости проекций, то на эпюре одна ее проекция совпадает с самой точкой, а другая лежит на оси проекций (В  П₁ рис. 3, 4).

Построить три проекции точки, имеющей координаты 30, 40, 30 (рис.5) (X, Y, Z).

По оси Х откладываем 30, проводим линию связи перпендикулярно оси ХО, на которой параллельно оси Y откладываем 40 - получаем А₁, параллельно оси Z - 30, получаем точку А₂.

Точка А₃ строится по двум уже построенным проекциям А₁ и А₂.

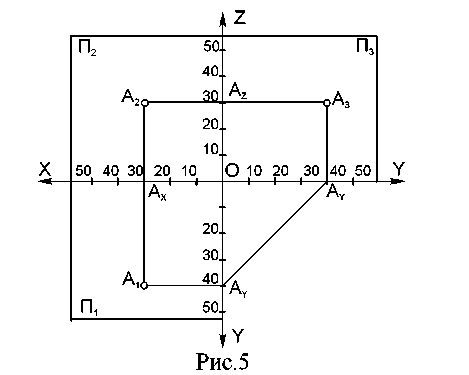
Рис. 5

1.6. Вопросы для самопроверки.

1. В чём заключается операция проецирования точки на плоскость проекций?

2. Какие основные виды проецирования геометрических форм на плоскость Вам известны?

3. Какие виды параллельных проекций вы знаете?

4. Перечислите основные свойства центральных проекций.

5. Перечислите основные свойства параллельных проекций

6. . Что называют ортогональной проекцией точки?

7. Как образуются проекции точки на плоскостях П₁, П₂, П₃?

8. В чём заключается метод построения комплексного чертежа?

9. Что называют координатами точки пространства в декартовой системе координат, и какие координаты на эпюре определяют ее горизонтальную, фронтальную и профильную проекции?

10. Как построить комплексный чертёж точки по её координатам?