2.3.1. Зв'язок між геодезичною, приведеною і геоцентричною широтами.

Для того щоб встановити зв'язок геодезичної широти В з приведеною и, розглянемо який-небудь меридіан, наприклад, такий, площиною якого є площина zx (див. рис.2.2). Для цього меридіана L=const і його рівняння в параметричній формі отримаємо із рівнянь (2.10)

Тангенс кута, утвореного нормаллю з віссю х (рис.2.4), рівний похідній взятій з оберненим знаком, тобто

,

або

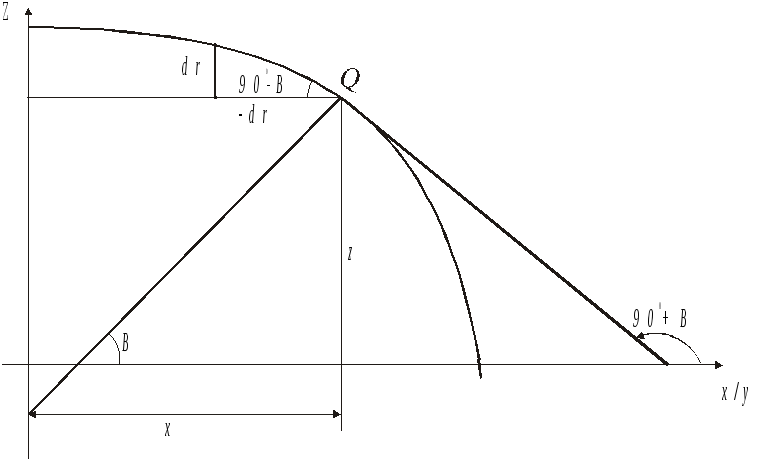
Рис. 2.4

Із останньої формули легко можна отримати

Ввівши позначення

отримаємо наступні формули зв'язку між геодезичною та приведеноюширотами

(2.18)

Приймаючи до уваги третю формулу (2.5), отримаємо

(2.19)

На основі формул (2.15) та (2.19) зв'язок між геоцентричною широтою та геодезичноюбуде наступним

(2.20)

Для подальшого викладу нам будуть необхідні ще наступні залежності, що легко отримуються із (2.19)

(2.21)

Якщо ввести позначення

(2.22)

то формули (2.21) будуть мати наступний вид

(2.23)

Згідно формул (2.23) і (2.18) можна записати зв'язок між величинами V та W

.(2.24)

Із формули (2.24) з врахуванням (2.22) та зв'язку між ексцентриситетами (перша формула із 2.5) отримаємо вираз для V у функції геодезичної широти

2.25)

Функції V та W називають ще основними сфероїдними функціями геодезичної широти.

У сфероїдній геодезії часто використовується позначення

(2.26)

тоді

(2.27)

2.3.2. Зв’язки між різними видами координат.

Між просторовими прямокутними (декартовими) та геоцентричнимикоординатами, на основі формул (2.10)

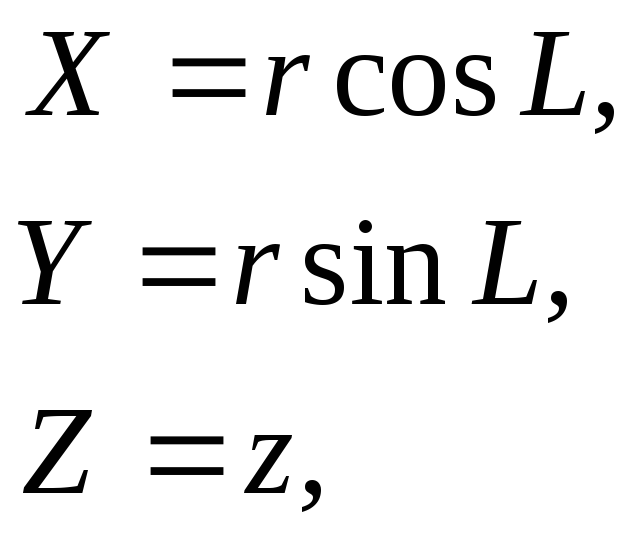
та отриманих співвідношень (2.16), існують прості математичні залежності

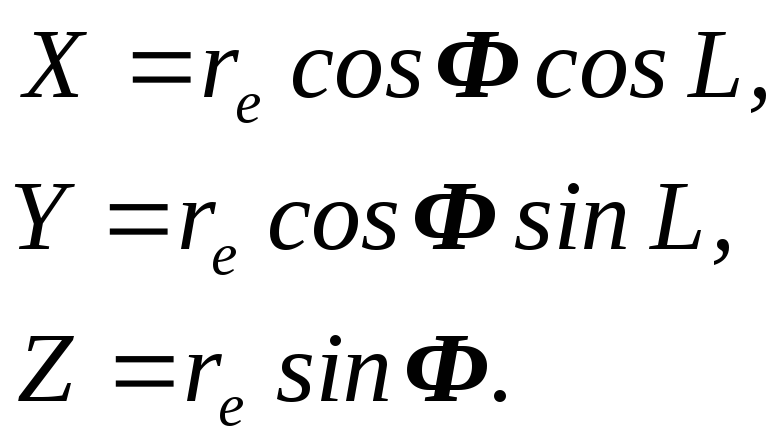(2.28)

Радіус-вектор еліпсоїда визначається із (2.17).

Обернені залежності, на основі (2.28), будуть мати наступний вид

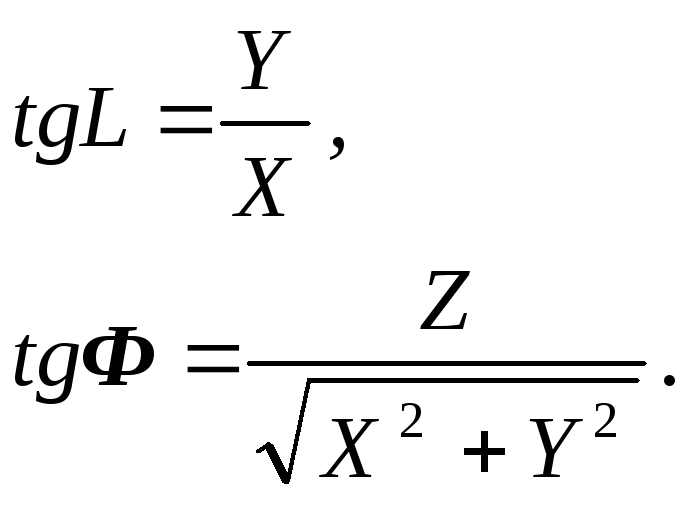(2.29)

Між просторовими прямокутними координатами X,Y,Z , приведеною широтою и та геодезичною довготою L на основі формул (2.10) та отриманих співвідношень між великою та малою півосями (див. третю формулу (2.5)), існують наступні залежності

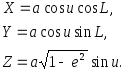(2.30)

Обернені залежності, на основі (2.30), будуть мати наступний вид

(2.31)

Враховуючи співвідношення (2.20) та (2.30), для поверхневих еліпсоїдних координат B,L та декартових X,Y,Z формули зв'язку мають вид

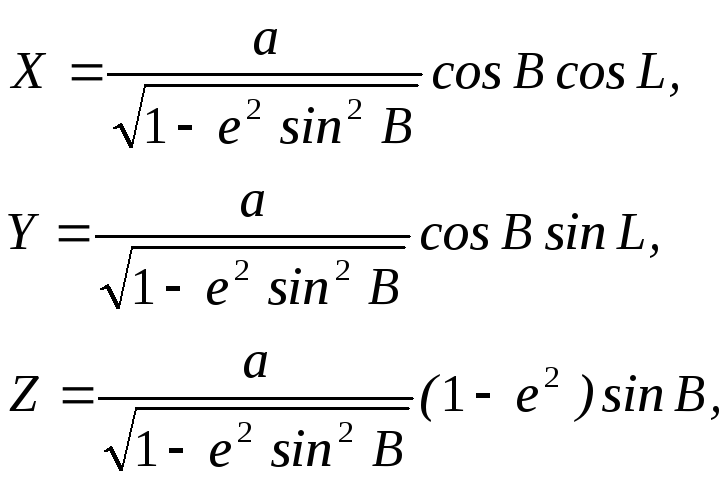
Вираз позначимо черезі, як буде видно із подальшого викладу (параграф 2.4), це є рівняння для радіуса кривини першого вертикалу заданої точки на поверхні еліпсоїда у функції геодезичної широти. Остаточно, формули зв’язку будуть наступними:

(2.32)

Обернені залежності будуть мати наступний вид

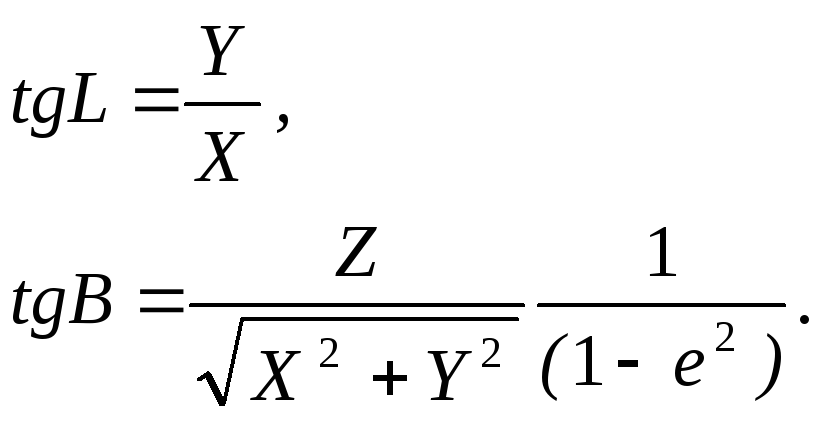(2.33)

Перша формула (2.33) отримана простим перетворенням (шляхом ділення другої формули (2.32) на першу). Друга формула (2.33) отримана наступним чином. Із перших двох формул (2.32) отримаємо

Поділивши третє рівняння (2.32) на отримане, дістанемо остаточно друге рівняння (2.33).

Зв’язок між геодезичними координатами та декартовимиотримаємо наступним чином. Спроектуємо висоту(див.рис.1.3) на відповідні осі (рис.1.4). Тоді проекції висоти будуть виражені залежностями

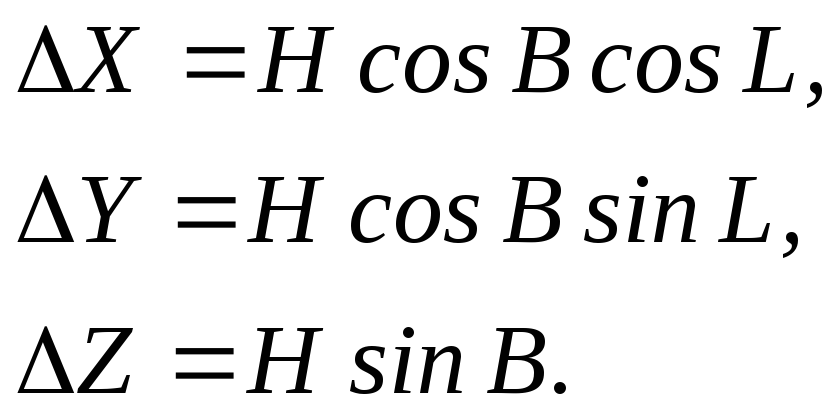
Або

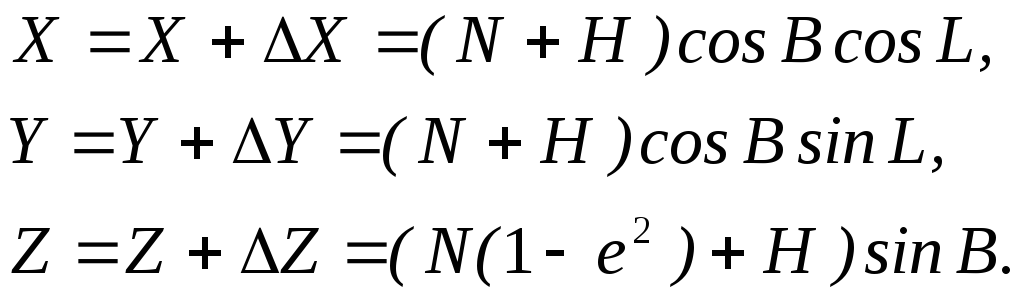(2.34)

Обернені залежності будуть мати наступний вид

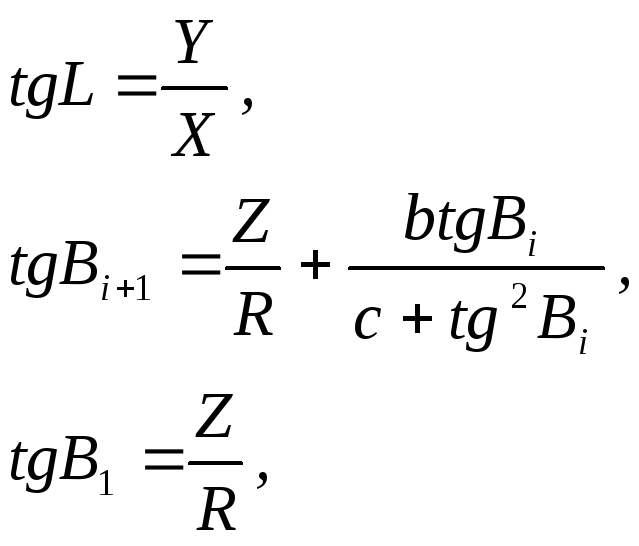
(2.35)

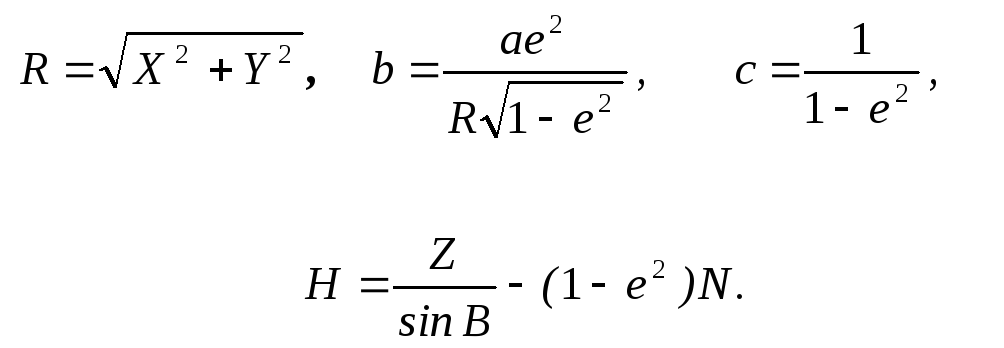
Вираз для обчислення довготи знаходимо аналогічно (2.33), а обчислення широти, як видно із (2.35) вимагає застосування процесу наближень. Формула дляотримана наступним чином.На основі рівнянь (2.34), після нескладних перетворень, можемо отримати

,

а також

.

Тоді

,

або

(2.36)

Поділимо чисельник і знаменник у другому доданку (2.36) на і в результаті перетворень отримаємо

,

а домноживши знаменник другого доданку ще на та після деяких перетворень, остаточно отримаємо формулу, яка після відповідних позначень буде відповідати (2.35).

Що стосується переходу від поверхневих еліпсоїдних координат B,L до плоских x,y, то вид формул залежить від способу зображення (проекції) поверхні еліпсоїда на площині. Для проекції Гаусса-Крюгера формули зв'язку приведенні при розгляді відповідної теми у розділі 4.

4. Головні радіуси кривизни в даній точці еліпсоїда

В будь-якій точці поверхні еліпсоїда обертання головними нормальними перерізами є:

1. меридіальний переріз, тобто нормальний переріз, що проходять через задану точку і полюси еліпсоїда;

2. переріз першого вертикалу, що проходить через точку і перпендикулярний до меридіального перерізу точки.

Радіус кривини меридіального перерізу буде радіусом кривини плоскої кривої, від обертання якої утворилась дана поверхня обертання. У сфероїдній геодезії він позначається буквою М. Радіус кривини другого головного перерізу - N. Вказані радіуси аналогічні радіусам та(див. розділ 1, п.1.6).

Згідно теореми Меньє (1.6), радіус кривини першого вертикалу буде рівний радіусу паралеліr , поділеному на косинус кута між площиною паралелі та нормаллю до поверхні

(2.37)

Це означає, що радіус кривини головного перерізу, перпендикулярного до меридіального, рівний відрізку нормалі до поверхні від поверхні до осі обертання (рис 2.5).

Радіуси кривини M та N , як функції широти В даної точки, застосовуються в багатьох теоретичних і практичних розрахунках. У функції широти радіус кривини меридіана М може бути виражений через формули (1.2) або через коефіцієнти першої та другої квадратичних форм поверхні (1.7).

На основі другої групи формул (1.2) та з врахуванням рівняння (2.10) в редакції (2.13) для радіуса кривини меридіана запишемо

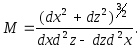
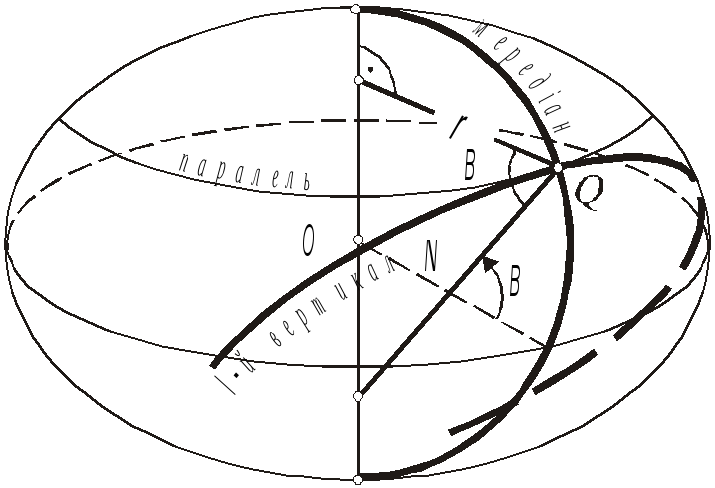
Рис. 2.5

Підставивши у вищенаведену формулу значення похідних, отримаємо вираз для радіуса кривини

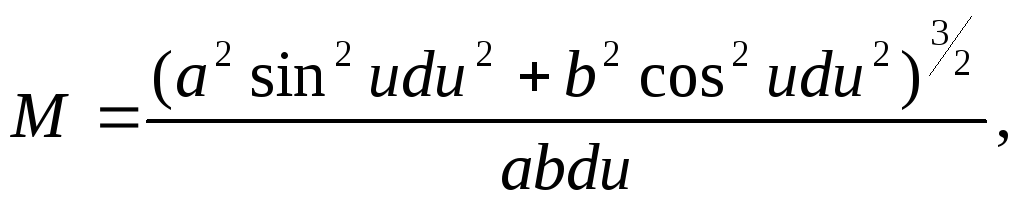
або

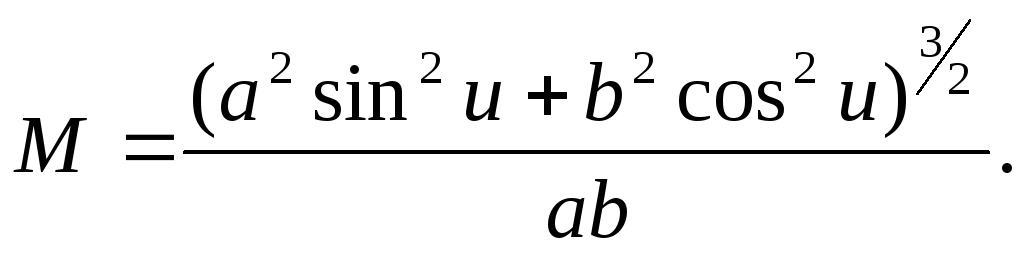(2.38)

Вираз (2.38) можна перетворити

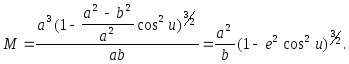
З врахуванням першої формули (2.20) та формули (2.21), остаточний вираз для радіуса кривини меридіана буде мати вид

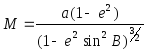. (2.39)

З врахуванням (2.11) вираз для радіуса кривини першого вертикалу буде

а використовуючи першу із формул (2.20), остаточно отримаємо

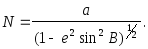(2.40)

Величини М та N характеризують форму поверхні еліпсоїда в околицях даної точки і в подальшому постійно будуть нами використовуватися. Графічно, залежність радіусів кривини івід широти, показана на рис. 2.6 а) і б) відповідно.

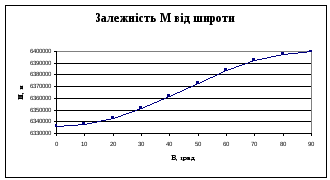
а

)

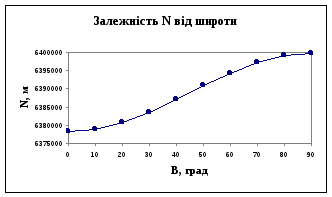
б)

Рис.2.6

Більшим за значенням є радіус кривини . Дійсно, згідно формул (2.39) і (2.40), маємо

.

тільки при В=90 , тобто на полюсі, де радіус кривини

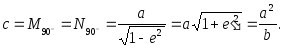(2.41)

Відношення різниці головних радіусів кривини до меншого із них може бути виражений формулою

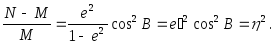
Величина ² характеризує відступ форми еліпсоїда в околицях даної точки від сфери.

Досить часто застосовуються і інші вирази для радіусів М та N

(2.42)