
- •С.Г.Савчук
- •Передмова
- •Передмова до другого видання
- •Список літератури
- •1.2. Математичні та фізичні моделі Землі.
- •1.3. Системи координат, що застосовуються у вищій геодезіі.
- •1.4. Основи теорії поверхонь.
- •Розділ 2 геометрія земного еліпсоїда
- •Таблиця 2.1
- •2.3.1. Зв'язок між геодезичною, приведеною і геоцентричною широтами.
- •2.3.2. Зв’язки між різними видами координат.
- •З використанням введених позначень, формулу (1.8) із розділу 1, запишемо у виді
- •Рис 2.8
- •На основі (2.60) отримаємо
- •Розділ 3 розв’язування геодезичних задач
- •3.1. Види геодезичних задач.
- •3.2. Короткі історичні відомості.
- •3.4.1. Розв’язування сфероїдних трикутників.
- •Сферичний надлишок
- •Таблиця 3.1
- •Способи розв’язування малих сфероїдних трикутників а) за формулами сферичної тригонометрії
- •Б) за теоремою Лежандра
- •Згідно теореми Лежандра, значення кутів плоского (лежандрового) трикутника буде
- •В) за способом аддитаментів
- •Позначивши
- •Г) за виміряними сторонами
- •3.4.2. Розв’язування головних геодезичних задач а) на поверхні сфери
- •Б) на поверхні еліпсоїда
- •В) в просторі
- •3.5. Диференційні формули.
- •3.5.1. Диференційні формули для геодезичної лінії.
- •3.5.2. Диференційні формули для довільної точки простору.
- •3.5.3. Диференційні формули для системи геодезичних координат.
- •3.5. Диференційні формули.
- •3.5.1. Диференційні формули для геодезичної лінії.
- •3.5.2. Диференційні формули для довільної точки простору.
- •3.5.3. Диференційні формули для системи геодезичних координат.
- •3.7.1.Алгоритм та числовий приклад розв'язування прямої і оберненої геодезичних задач на поверхні сфери.
- •Обернена геодезична задача
- •Обернена геодезична задача
- •3.7.5. Алгоритм та числовий приклад розв'язування прямої та оберненої геодезичних задач на поверхні еліпсоїда на основі чисельного методу (формул Рунге-Кутта) а) алгоритм
- •Пряма геодезична задача
- •Обернена геодезична задача
- •Б) числовий приклад
- •Пряма геодезична задача
- •Обернена геодезична задача
- •3.7.6. Алгоритм та числовий приклад розв'язування прямої та оберненої геодезичних задач в просторі.
- •Обернена геодезична задача
- •Розділ 4 плоскі прямокутні координати гаусса-крюгера
- •4.1. Плоскі координати в геодезії.
- •4.4. Перетворення полярних координат.
- •4.5. Формули проекції Гаусса-Крюгера
- •4.5.2. Формули для обчислення зближення меридіанів
- •4.5.3. Формули для обчислення масштабу проекції
- •Таблиця 4.2
- •Таблиця 4.3
- •Таблиця 4.4
- •Таблиця 4.5
- •Тоді, згідно формули (4.37), для відносного спотворення відстаней, напишемо
- •Таблиця 4.6
- •Таблиця 4.11
- •4.8. Перетворення координат Гаусса-Крюгера із зони в зону.
- •Розділ 5 основи теоретичної геодезії
- •5.1. Сучасні поняття про фігуру Землі та її зовнішнє гравітаційне поле
- •5.2.1. Астрономо-геодезичні відхилення прямовисних ліній
- •5.2.2. Гравіметричні відхилення прямовисних ліній
- •5.2.3. Інтерполювання відхилень прямовисних ліній
- •5.3. Визначення відступів геоїда (квазігеоїда)
- •5.3.1. Астрономічне нівелювання
- •5.3.2. Астрономо-гравіметричне нівелювання
- •5.4. Система висот в геодезії
- •5.4.1. Поняття висоти
- •5.4.1. Ортометричні висоти
- •5.4.3. Нормальні висоти
- •5.4.4. Динамічні висоти
- •5.5.1. Поняття про редукційну задачу
- •5.5.2. Редукування лінійних вимірів
- •5.5.3. Редукування виміряних горизонтальних напрямів
- •5.6.1. Методи виводу розмірів земного еліпсоїда за градусними вимірюваннями
- •5.6.2.Встановлення вихідних геодезичних дат
- •5.6.3. Сучасні підходи до визначення параметрів фігури Землі
З використанням введених позначень, формулу (1.8) із розділу 1, запишемо у виді
![]() (2.43)
(2.43)
Дана
формула встановлює залежність радіуса
кривини нормального перерізу, проведеного
під азимутом
![]() ,
від радіуса кривини меридіана та першого
вертикала.
,
від радіуса кривини меридіана та першого
вертикала.
Середнє геометричне значення із головних радіусів кривини
![]() (2.44)
(2.44)
називається середнім радіусом кривини еліпсоїда обертання, а рівняння (2.44) є наслідком формули (1.9).

Рис.2.7
При
розв’язуванні
деяких задач Землю приходиться приймати
за кулю. Якщо це робиться для досить
наближених розрахунків, радіус кулі
![]() приймається рівним 6 371 км, в інших
випадках можна прийняти
приймається рівним 6 371 км, в інших
випадках можна прийняти![]() .
.
Лінійний елемент поверхні еліпсоїда.
Через дану точку на поверхні еліпсоїда можна провести низку різних ліній. Кожна з цих ліній певним чином зорієнтована відносно однієї з координатних ліній, а саме меридіана. Кут орієнтування, тобто кут між дотичними, проведеними до меридіана в північному напрямі та заданою лінією, називається геодезичним азимутом А. Він відраховується від меридіана в сторону руху годинникової стрілки. Один і той азимут може мати і декілька різних ліній. Це буде в тому випадку, коли ці лінії мають спільну дотичну в даній точці., наприклад, паралель і перший вертикал в заданій точці поверхні еліпсоїда мають однаковий азимут, який дорівнює 900 (або 2700), хоча розташовані вони в різних площинах.
Диференціал дуги ds довільної кривої на поверхні еліпсоїда називається лінійним елементом поверхні еліпсоїда.
На поверхні еліпсоїда координатні лінії мають своє позначення: Х – довжина дуги меридіана від екватора (в сторону полюса) до даної точки; Y – довжина дуги паралелі від середнього (початкового) меридіана до даної точки.
Відомо,
що для будь-якої кривої радіус її кривини
в даній точці дорівнює відношенню
диференціала дуги кривої до до диференціалу
кута між дотичними до кривої в крайніх
точках цієї дуги. Якщо позначити
диференціал дуги меридіана через
![]() ,
а паралелі через
,
а паралелі через![]() ,
диференціал кута між дотичними до
крайніх точок елемента дуги меридіана
через
,
диференціал кута між дотичними до
крайніх точок елемента дуги меридіана
через![]() ,
а паралелі через
,
а паралелі через![]() ,
то, згідно вище зазначеного, для
диференціалів дуг меридіана та паралелі
отримаємо відповідно
,
то, згідно вище зазначеного, для
диференціалів дуг меридіана та паралелі
отримаємо відповідно
![]()
![]()
Спроектувавши лінійний елемент на координатні лінії (лінії меридіанів та паралелей), отримаємо (див. рис 2.8)
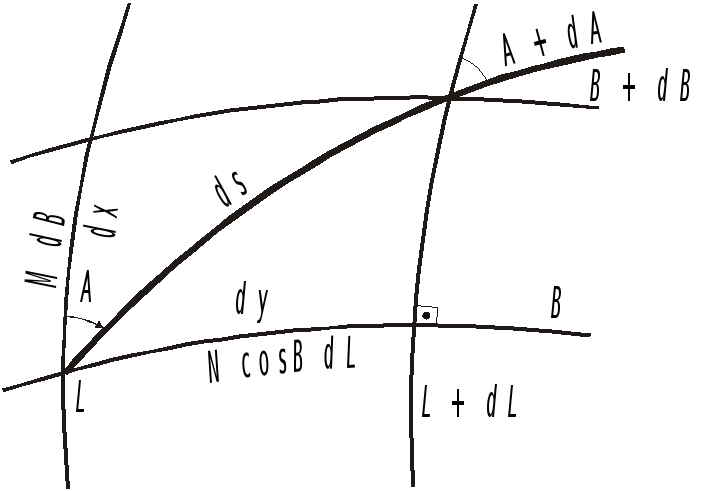
Рис 2.8
![]() (2.45)
(2.45)
Звідки,
![]() (2.46)
(2.46)
Отримане рівняння (2.46) є аналогом рівняння (1.4) для поверхні еліпсоїда обертання, тобто є першою квадратичною формою поверхні еліпсоїда.
Характер зміни довготи та широти при переміщенні вздовж будь-якої лінії на поверхні еліпсоїда, може бути виражений наступними диференціальними рівняннями, що випливають із (2.45)
![]() (2.47)
(2.47)
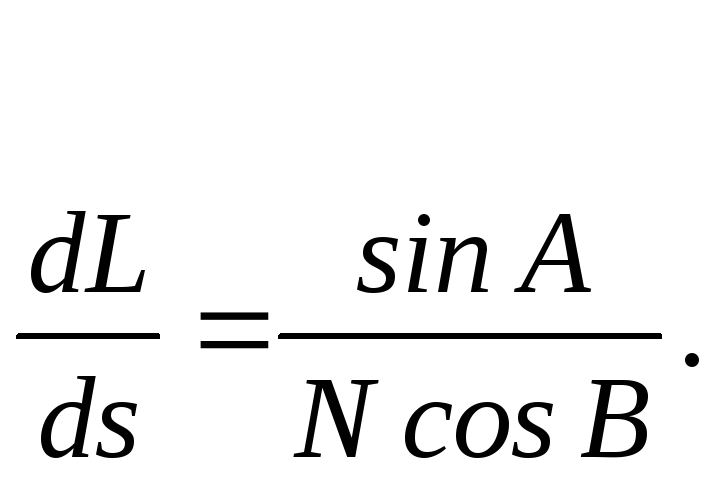 (2.48)
(2.48)
Серед цих формул відсутній вираз, що характеризує зміну азимута А в залежності від переміщення вздовж лінії на величину ds. Справа в тому, що ця залежність не буде однаковою для всіх ліній, тоді як приведенні вище формули відносяться до будь-якої лінії на поверхні.
2.6. Довжини дуг меридіана та паралелі. Площа сфероїдної трапеції.
Поскільки у формулі лінійного елемента поверхні еліпсоїда (2.46) кожна складова в правій частині є квадрат диференціала дуги координатної лінії, то звідти отримаємо наступні вирази для довжин дуг меридіана та паралелі:

 (2.49)
(2.49)
Рис. 2.9
На практиці також часто виникає необхідність обчислення площі частин поверхні еліпсоїда (сфероїдних трапецій), які представляють площі знімальних трапецій.
Сфероїдною трапецією називається частина поверхні еліпсоїда, обмежена меридіанами і паралелями (рис 2.10).
Елемент
площі сфероїдної трапеції dP
визначається добутком диференціалів
дуг координатних ліній:
dP=dXdY.
Замінивши
dX
і dY
їх значеннями за формулами (2.45) отримає-мо
![]()
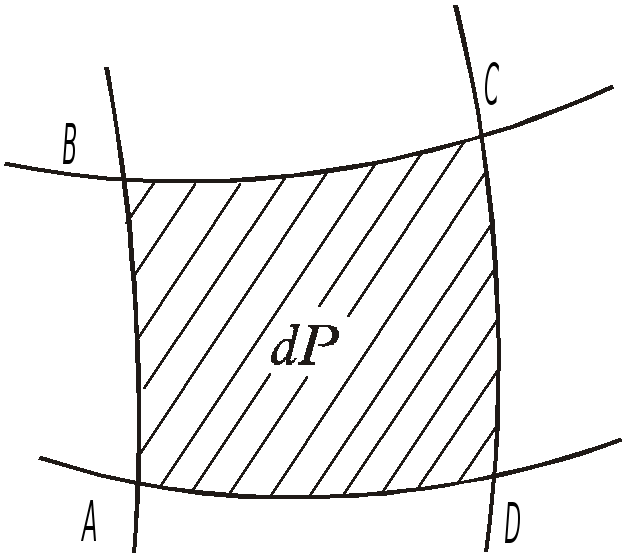
Рис.2.10
де М і N визначаються формулами (2.39) і (2.40) відповідно.
Тоді площа сфероїдної трапеції визначається подвійним інтегралом:
 (2.50)
(2.50)
Обчислення довжини дуги меридіана
Обчислення довжини дуги меридіана Х, згідно (2.49), зводиться до знаходження еліптичного інтегралу
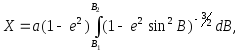 (2.51)
(2.51)
який в елементарних функціях не береться. Одним із класичних шляхів його знаходження є розклад підінтегрального виразу в біномінальний ряд з подальшим почленним інтегруванням. Маємо
![]()
Замінивши в цьому виразі парні степені синуса косинусами кратних дуг згідно відомих рівнянь
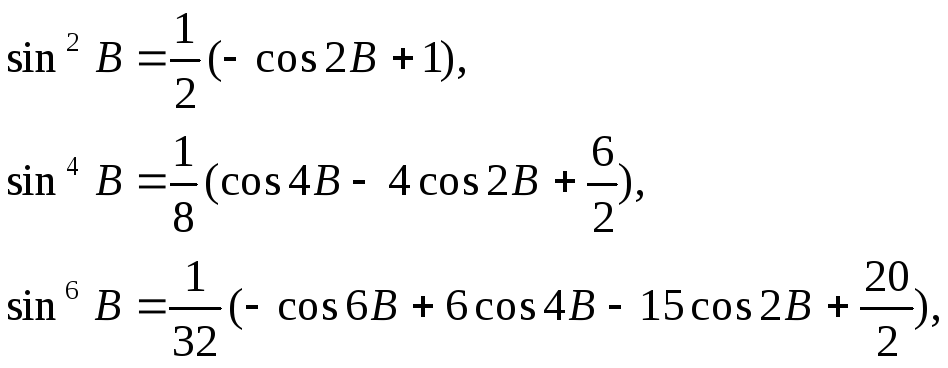
та
згрупувавши постійні члени і позначивши
їх буквами
![]() ,
отримаємо
,
отримаємо
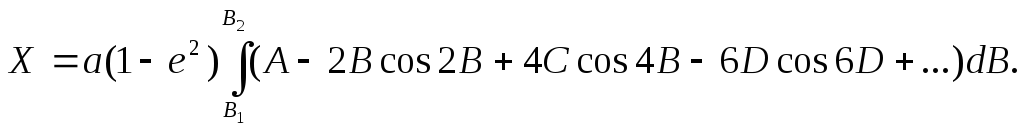
Звідси, після почленного інтегрування і підстановки границь, знайдемо остаточно
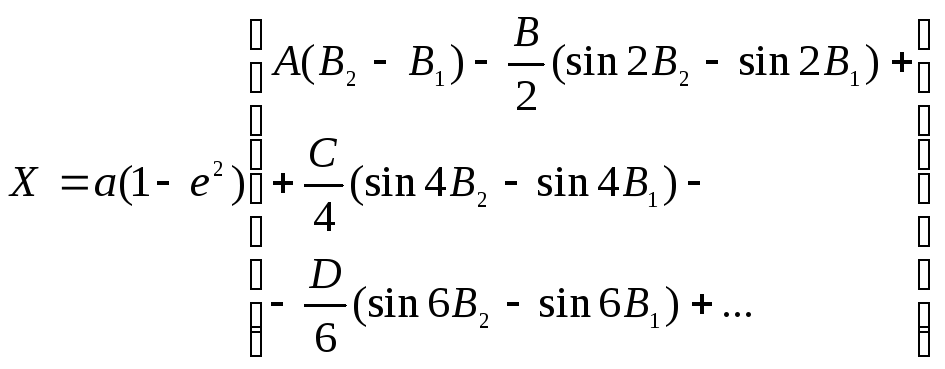 (2.52)
(2.52)
Коефіцієнти
![]() визначаються із наступних виразів,
основним аргументом яких є ексцентриситет
еліпсоїда
визначаються із наступних виразів,
основним аргументом яких є ексцентриситет
еліпсоїда
 (2.53)
(2.53)
За формулою (2.52) можна знайти довжину дуги земного меридіана будь-якої довжини, взявши при цьому необхідну кількість членів розкладу.
Для
обчислення довжини дуги меридіана від
екватора (![]() )
до будь-якої паралелі з широтоюВ
, формула (2.52) отримає наступний вид
)
до будь-якої паралелі з широтоюВ
, формула (2.52) отримає наступний вид
![]() (2.54)
(2.54)
Формулу (2.54) можна представити ще в такому виді
![]() ,
(2.55)
,
(2.55)
де
коефіцієнти
![]() визначаються через параметри прийнятого
еліпсоїда
визначаються через параметри прийнятого
еліпсоїда
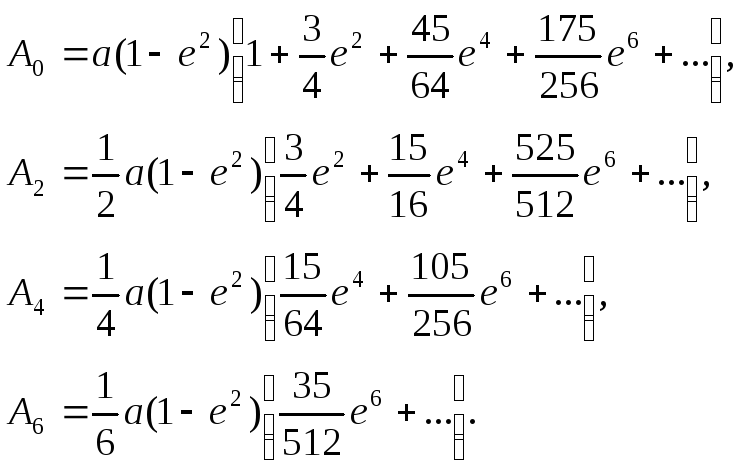 (2.56)
(2.56)
Формулами (2.55) і (2.56) ми будемо користуватися в розділі 4.
Вираз для довжини дуги меридіана при малих відстаннях (довжини сторін або ланки тріангуляції 1 класу) можна отримати на основі застосування формули Тейлора з введенням середнього аргумента.
Позначимо
довжини дуг меридіанів від екватора до
точок з широтою
![]() та
та![]() через
через![]() та
та![]() .
Крім того,
.
Крім того,
![]() .
Тоді можна написати
.
Тоді можна написати
![]() (2.57)
(2.57)
Приймаючи
різницю широт між двома точками
![]() малою величиною, запишемо ряд за степенямиВ
малою величиною, запишемо ряд за степенямиВ
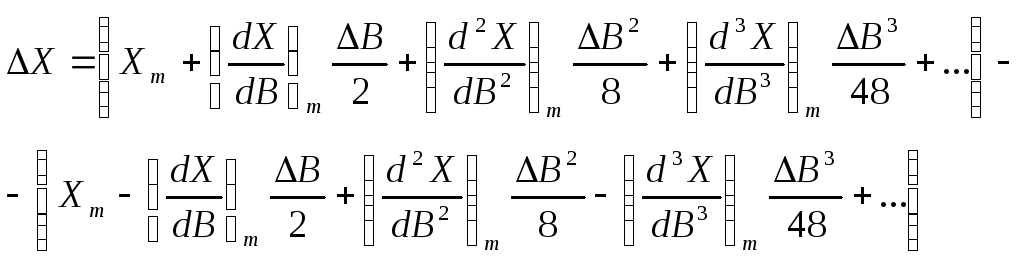 ,
,
або
![]() (2.58)
(2.58)
Індекс
“m”
при коефіцієнтах цього ряду означає,
що вони обчислюються за середнім
аргументом
![]() .
Похідні
.
Похідні![]() (і=1,3),
можна знайти на основі першої формули
(2.49) послідовним диференціюванням:
(і=1,3),
можна знайти на основі першої формули
(2.49) послідовним диференціюванням:
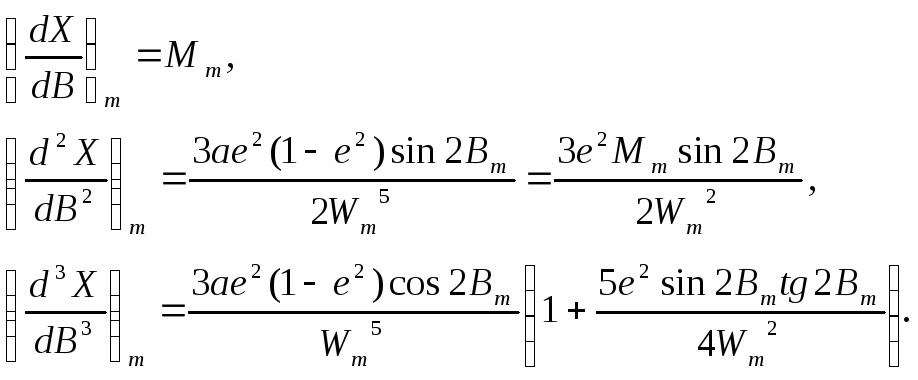
Тут
![]() визначається
формулою (2.21).
визначається
формулою (2.21).
Останній
вираз з точністю до членів з
![]() можна
записати
можна
записати
![]()
Підставивши значення похідних у (2.58), остаточно отримаємо
![]() ,(2.59)
,(2.59)
де Mm обчислюється через Bm за формулою (2.39).
Другий
член в правій частині формули (2.59) на
широтах 45-55
складає всього лише 0,002м при
![]() .
Тому для малих різниць широтВ,
дугу меридіана можна розглядати як
дугу кола з центральним кутом, який
рівний різниці широт її крайніх точок
, і описану радіусом меридіанного
перерізу, рівному Mm
,
тобто
.
Тому для малих різниць широтВ,
дугу меридіана можна розглядати як
дугу кола з центральним кутом, який
рівний різниці широт її крайніх точок
, і описану радіусом меридіанного
перерізу, рівному Mm
,
тобто
![]() (2.60)
(2.60)
Наближенене
значення інтегралу
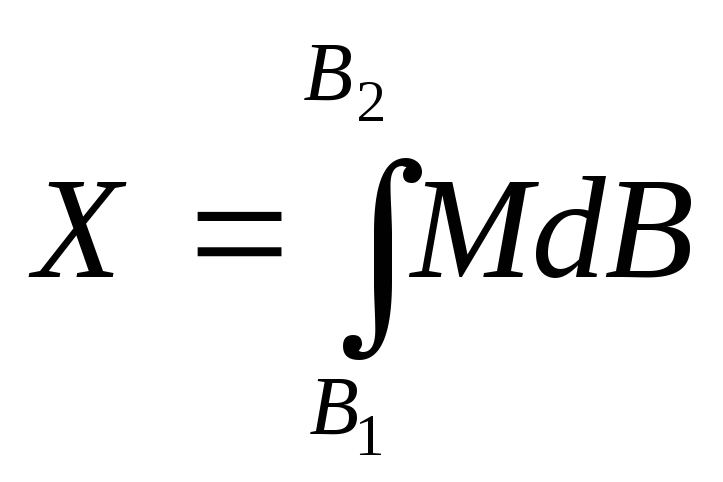 можна обчислити на основі застосування
чисельних методів розв'язування означених
інтегралів. Серед них: формули трапецій,
Сімпсона, Гаусса, Чебишева тощо. В розділі
1 приведено два методи обчислення
інтегралу
можна обчислити на основі застосування
чисельних методів розв'язування означених
інтегралів. Серед них: формули трапецій,
Сімпсона, Гаусса, Чебишева тощо. В розділі
1 приведено два методи обчислення
інтегралу![]() :
формули (1.10) для методу Сімпсона та
(1.11) для методу Гаусса. Застосуємо вказані
формули для обчислення довжини дуги
меридіана між точками з широтами
:
формули (1.10) для методу Сімпсона та
(1.11) для методу Гаусса. Застосуємо вказані
формули для обчислення довжини дуги
меридіана між точками з широтами![]() та
та![]() .
.
В
першому випадку розділимо інтервал
інтегрування на дві частини з кроком
![]() .
Для кожної вузлової точки
.
Для кожної вузлової точки![]() з кроком
з кроком![]() за аргументом
за аргументом![]() знаходимо значення підінтегральної
функції
знаходимо значення підінтегральної
функції![]() .
Тоді, згідно (1.10), отримаємо
.
Тоді, згідно (1.10), отримаємо
![]() .
(2.61)
.
(2.61)
При
застосуванні формули (1.11) виберемо дві
вузлові точки (і=2).
З врахуванням даних табл.1.1, визначимо
аргументи функції
![]() .
При
.
При![]() аргументом буде значення широти
аргументом буде значення широти![]() ,
а при
,
а при![]() -
-![]() .
Остаточно, формула для обчислення
довжини дуги меридіана методом Гаусса,
буде
.
Остаточно, формула для обчислення
довжини дуги меридіана методом Гаусса,
буде
![]() .
(2.62)
.
(2.62)
Вказані
формули є рівноточними і дозволяють
обчислювати довжину дуги меридіана при
різниці широт до
![]() з похибкою
з похибкою![]() м.
Для розширення широтного діапазону
треба ділити інтервал інтегрування на
більшу кількість частин (для методу
Сімпсона) або вибирати більшу кількість
вузлових точок (для методу Гаусса).
м.
Для розширення широтного діапазону
треба ділити інтервал інтегрування на
більшу кількість частин (для методу
Сімпсона) або вибирати більшу кількість
вузлових точок (для методу Гаусса).
Можна
поставити обернену задачу: при відомій
довжині дуги меридіана
![]() і її середній широті чи
і її середній широті чи![]() ,
знайти різницю широт кінцевих точок чи
широту
,
знайти різницю широт кінцевих точок чи
широту![]() .
.
