
- •С.Г.Савчук
- •Передмова
- •Передмова до другого видання
- •Список літератури
- •1.2. Математичні та фізичні моделі Землі.
- •1.3. Системи координат, що застосовуються у вищій геодезіі.
- •1.4. Основи теорії поверхонь.
- •Розділ 2 геометрія земного еліпсоїда
- •Таблиця 2.1
- •2.3.1. Зв'язок між геодезичною, приведеною і геоцентричною широтами.
- •2.3.2. Зв’язки між різними видами координат.
- •З використанням введених позначень, формулу (1.8) із розділу 1, запишемо у виді
- •Рис 2.8
- •На основі (2.60) отримаємо
- •Розділ 3 розв’язування геодезичних задач
- •3.1. Види геодезичних задач.
- •3.2. Короткі історичні відомості.
- •3.4.1. Розв’язування сфероїдних трикутників.
- •Сферичний надлишок
- •Таблиця 3.1
- •Способи розв’язування малих сфероїдних трикутників а) за формулами сферичної тригонометрії
- •Б) за теоремою Лежандра
- •Згідно теореми Лежандра, значення кутів плоского (лежандрового) трикутника буде
- •В) за способом аддитаментів
- •Позначивши
- •Г) за виміряними сторонами
- •3.4.2. Розв’язування головних геодезичних задач а) на поверхні сфери
- •Б) на поверхні еліпсоїда
- •В) в просторі
- •3.5. Диференційні формули.
- •3.5.1. Диференційні формули для геодезичної лінії.
- •3.5.2. Диференційні формули для довільної точки простору.
- •3.5.3. Диференційні формули для системи геодезичних координат.
- •3.5. Диференційні формули.
- •3.5.1. Диференційні формули для геодезичної лінії.
- •3.5.2. Диференційні формули для довільної точки простору.
- •3.5.3. Диференційні формули для системи геодезичних координат.
- •3.7.1.Алгоритм та числовий приклад розв'язування прямої і оберненої геодезичних задач на поверхні сфери.
- •Обернена геодезична задача
- •Обернена геодезична задача
- •3.7.5. Алгоритм та числовий приклад розв'язування прямої та оберненої геодезичних задач на поверхні еліпсоїда на основі чисельного методу (формул Рунге-Кутта) а) алгоритм
- •Пряма геодезична задача
- •Обернена геодезична задача
- •Б) числовий приклад
- •Пряма геодезична задача
- •Обернена геодезична задача
- •3.7.6. Алгоритм та числовий приклад розв'язування прямої та оберненої геодезичних задач в просторі.
- •Обернена геодезична задача
- •Розділ 4 плоскі прямокутні координати гаусса-крюгера
- •4.1. Плоскі координати в геодезії.
- •4.4. Перетворення полярних координат.
- •4.5. Формули проекції Гаусса-Крюгера
- •4.5.2. Формули для обчислення зближення меридіанів
- •4.5.3. Формули для обчислення масштабу проекції
- •Таблиця 4.2
- •Таблиця 4.3
- •Таблиця 4.4
- •Таблиця 4.5
- •Тоді, згідно формули (4.37), для відносного спотворення відстаней, напишемо
- •Таблиця 4.6
- •Таблиця 4.11
- •4.8. Перетворення координат Гаусса-Крюгера із зони в зону.
- •Розділ 5 основи теоретичної геодезії
- •5.1. Сучасні поняття про фігуру Землі та її зовнішнє гравітаційне поле
- •5.2.1. Астрономо-геодезичні відхилення прямовисних ліній
- •5.2.2. Гравіметричні відхилення прямовисних ліній
- •5.2.3. Інтерполювання відхилень прямовисних ліній
- •5.3. Визначення відступів геоїда (квазігеоїда)
- •5.3.1. Астрономічне нівелювання
- •5.3.2. Астрономо-гравіметричне нівелювання
- •5.4. Система висот в геодезії
- •5.4.1. Поняття висоти
- •5.4.1. Ортометричні висоти
- •5.4.3. Нормальні висоти
- •5.4.4. Динамічні висоти
- •5.5.1. Поняття про редукційну задачу
- •5.5.2. Редукування лінійних вимірів
- •5.5.3. Редукування виміряних горизонтальних напрямів
- •5.6.1. Методи виводу розмірів земного еліпсоїда за градусними вимірюваннями
- •5.6.2.Встановлення вихідних геодезичних дат
- •5.6.3. Сучасні підходи до визначення параметрів фігури Землі
4.5.2. Формули для обчислення зближення меридіанів
Для
визначення зближення меридіанів
![]() скористаємось другою формулою (4.4)
скористаємось другою формулою (4.4)
![]() (4.22)
(4.22)
часткові похідні в якій знайдемо на основі формул (4.15). Отримаємо
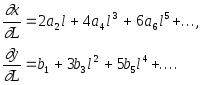 (4.22’)
(4.22’)
Підставивши значення похідних у (4.22), отримаємо
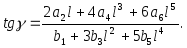 (4.23)
(4.23)
Значення
коефіцієнтів
![]() даються виразами (4.16), підставивши які
в (4.23) і виконавши елементарні математичні
перетворення, остаточно отримаємо
даються виразами (4.16), підставивши які
в (4.23) і виконавши елементарні математичні
перетворення, остаточно отримаємо
![]() (4.24)
(4.24)
Аналогічним чином можна знайти вираз для обчислення зближення меридіанів за плоскими прямокутними координатами, тільки при цьому за вихідну беруть другу формулу (4.8)
![]()
Приведемо остаточну формулу для зближення меридіанів у функції плоских прямокутних координат
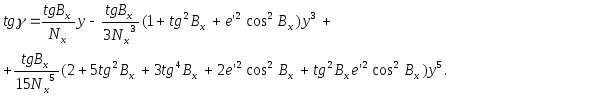 (4.25)
(4.25)
У
формулах (4.24) і (4.25) не враховано члени
з
![]() .
Точність приведених формул забезпечує
обчислення
.
Точність приведених формул забезпечує
обчислення![]() в
в![]() .
.
Знак
зближення меридіанів співпадає зі
знаком різниці довгот
![]() або
знаком
або
знаком![]() ,
тобто для точок, які розташовані на схід
від осьового меридіану, зближення
меридіанів завжди буде додатнім, а на
захід від нього - від’ємним.
,
тобто для точок, які розташовані на схід
від осьового меридіану, зближення
меридіанів завжди буде додатнім, а на
захід від нього - від’ємним.
4.5.3. Формули для обчислення масштабу проекції
Для знаходження формули масштабу зображення скористаємось формулою (4.5), яку представимо у вигляді
![]() (4.26)
(4.26)
Вирази для часткових похідних нами вже отримано - ф-ли (4.22’). Підставивши квадрати цих виразів у (4.26) і додавши їх, отримаємо
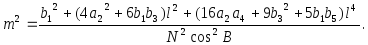
В
цій формулі збережено члени порядку
![]() .
З врахуванням виразів для
.
З врахуванням виразів для![]() (без
сфероїдних членів при
(без
сфероїдних членів при![]() )
та простих алгебраїчних перетворень
остаточно знаходимо
)
та простих алгебраїчних перетворень
остаточно знаходимо
![]() (4.27)
(4.27)
Як
видно із даної формули, при
![]() ,
тобто на осьовому меридіані, масштаб
проекції рівний одиниці. При віддалені
від осьового меридіана на схід і на
захід значення масштабу швидко зростає.
,
тобто на осьовому меридіані, масштаб
проекції рівний одиниці. При віддалені
від осьового меридіана на схід і на
захід значення масштабу швидко зростає.
Для отримання формули масштабу зображення у функції плоских прямокутних координат скористаємось другою формулою (4.19), яку, з прийнятими вище обмеженнями, запишемо
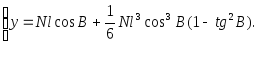
Застосовуючи
формули обертання ряду для
![]() ,
знайдемо
,
знайдемо
![]()
звідки з прийнятою точністю
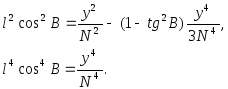
З врахуванням останніх двох виразів формулу (4.27) можна записати у наступному вигляді
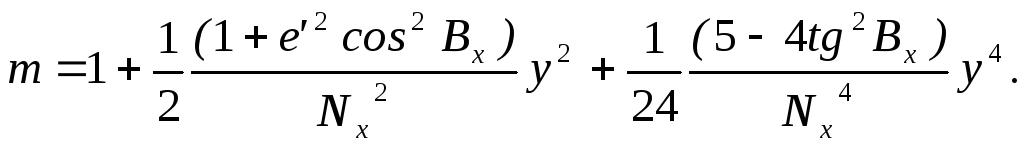 (4.28)
(4.28)
Оскільки
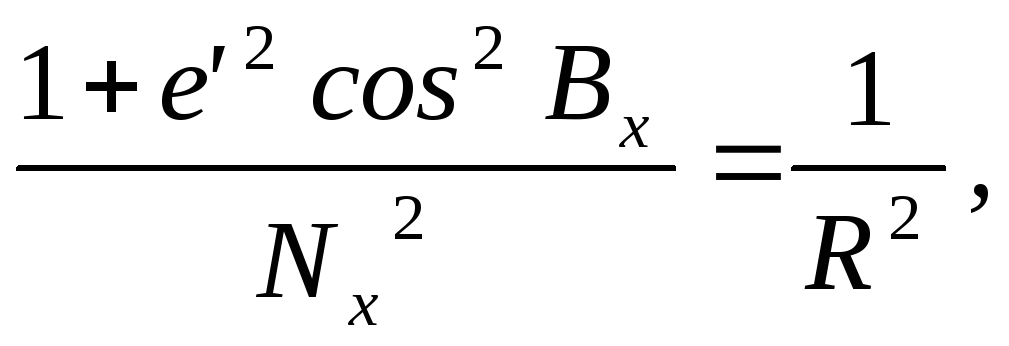
де
![]() - середній радіус кривини еліпсоїда, то
остаточно отримаємо
- середній радіус кривини еліпсоїда, то
остаточно отримаємо
![]() (4.29)
(4.29)
В
останньому члені формули (4.29) замість
![]() приведено
приведено![]() ,
що викличе похибку порядку
,
що викличе похибку порядку![]() на
сфероїдні члени, якими знехтувано у
членах порядку
на
сфероїдні члени, якими знехтувано у
членах порядку![]() .
.
Масштаб
зображення є дуже важливою характеристикою
конформної проекції. Згідно формули
(4.28) або (4.29) можна встановити величини
і розподіл лінійних спотворень при
переході з еліпсоїда на площину. Так
легко замітити, що із збільшенням
ординати
![]() лінійні
спотворення зростають пропорційно
лінійні
спотворення зростають пропорційно![]() ;
постійному значенню ординати
;
постійному значенню ординати![]() відповідає практично постійна величина
масштабу
відповідає практично постійна величина
масштабу![]() .
Величина радіуса
.
Величина радіуса
![]()
із зміною широти
змінюється звісно, але досить незначно.
Тому лінії рівних спотворень довжин в
проекції Гаусса-Крюгера розташовуються
практично паралельно осі абсцис на всій
смузі проекції від екватора до полюса,
а звідси виходить, що проекцію
Гаусса-Крюгера найбільш оптимально
застосовувати для зображення смуги,
яка витягнута на еліпсоїді з півдня на
північ. Межами такої смуги служать лінії
рівних спотворень довжин
![]() .
.
Формули для редукування напрямів і відстаней
Під редукуванням напрямів і відстаней розуміють перехід від напрямів і довжин геодезичних ліній на еліпсоїді до відповідних їм величин на площині. Редукція напрямів полягає у визначенні поправки за кривину зображення геодезичної лінії на площині, а редукція відстаней - знаходженні різниці довжини геодезичної лінії та хорди зображення геодезичної лінії. Після введення цих редукцій у виміряні величини, які приведені на поверхню еліпсоїда, ми отримаємо геодезичну мережу, редуковану з еліпсоїда на площину.
На практиці редукування мережі 1–го класу на площину проводиться тільки в окремих випадках і не має широкого розповсюдження, тому при виводі формул будемо орієнтуватися на мережі нижчих (2-4) класів.
Для редукування напрямів вважатимемо, що AB є геодезичною лінією на поверхні еліпсоїда в складі деякої замкнутої геодезичної фігури ABDC (рис. 4.5.б).
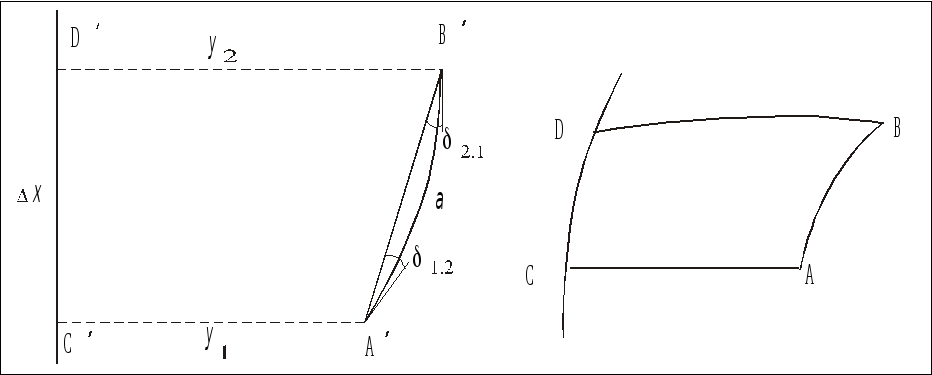
а) б)
Рис.4.5
Нехай
геодезична лінія AB
зображена на площині в виді кривої
![]() (рис.
4.5.а). Кути в точках
(рис.
4.5.а). Кути в точках
![]() і
і
![]() між дотичними до кривої і хордою
між дотичними до кривої і хордою
![]() позначимо через
позначимо через
![]() і
і
![]() .
Координати точок
.
Координати точок
![]() і
і
![]() позначимо через
позначимо через
![]() і
і
![]() .
Нехай точки
.
Нехай точки
![]() і
і
![]() є основами ординат точок
є основами ординат точок
![]() і
і
![]() відповідно. Із-за конформності проекції
фігури ABCD
і
A’B’C’D’
будуть подібними, а відповідні кути у
них рівними. Суми внутрішніх кутів
складуть:
відповідно. Із-за конформності проекції
фігури ABCD
і
A’B’C’D’
будуть подібними, а відповідні кути у
них рівними. Суми внутрішніх кутів
складуть:
на еліпсоїді
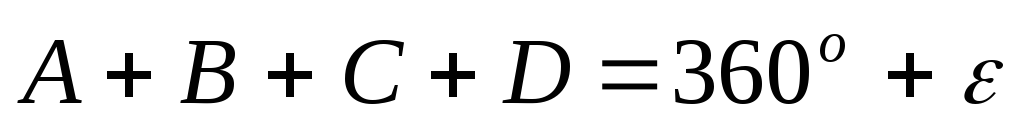 ;
;на площині
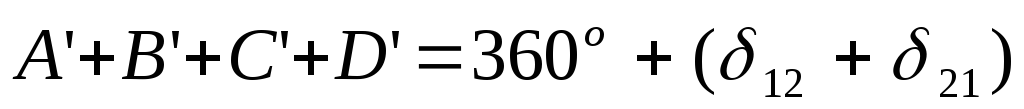 .
.
Значить,
![]() ,
тобто сферичний надлишок рівний сумі
поправок взаємнообернених напрямів.
Як відомо (див. розділ 3), сферичний
надлишок визначається формулою
,
тобто сферичний надлишок рівний сумі
поправок взаємнообернених напрямів.
Як відомо (див. розділ 3), сферичний
надлишок визначається формулою
![]()
де
![]() -
площа фігури A’B’C’D’;
-
площа фігури A’B’C’D’;
![]() .
.
Тоді
![]()
Приймаючи
наближено,
![]() ,
отримуємо
,
отримуємо
![]() .
(4.30)
.
(4.30)
На
практиці потрібно знати не тільки
величину кута
![]() для даного напряму, але і як ввести його
в цей напрям, щоб перейти на площині від
кривих ліній до їхніх хорд. Оскільки
відрахування кутів ведеться за ходом
годинникової стрілки, то із рис. 4.5.а)
легко видно, що для переходу від напряму
для даного напряму, але і як ввести його
в цей напрям, щоб перейти на площині від
кривих ліній до їхніх хорд. Оскільки
відрахування кутів ведеться за ходом
годинникової стрілки, то із рис. 4.5.а)
легко видно, що для переходу від напряму![]() до хорди
до хорди![]() кут
кут![]() при точці
при точці![]() потрібно відняти від напряму
потрібно відняти від напряму![]() ,
а при точці
,
а при точці![]() - додати до напряму
- додати до напряму![]() .
Отже,поправки
.
Отже,поправки
![]() і
і![]() у взаємні напрями мають протилежні
знаки:
у взаємні напрями мають протилежні
знаки:
![]() (4.31)
(4.31)
Формулами (4.31) користуються для редукування напрямів в тріангуляції 3 класу і нижче.
Поправки
за редукцію
![]() алгебраїчно
віднімаються
від виміряних напрямів.
алгебраїчно
віднімаються
від виміряних напрямів.
Значення редукованих плоских кутів A’,B’ і C’ за виміряними на фізичній поверхні і приведеними на еліпсоїд кутами A,B і C трикутника ABC отримують наступним чином
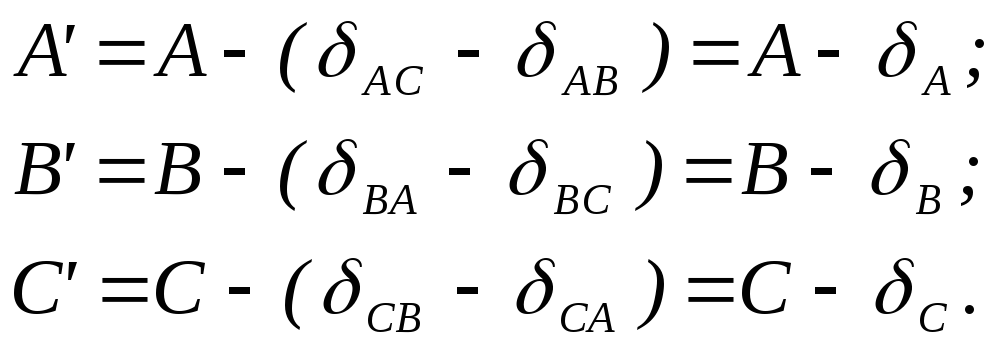
Сума
поправок за редукцію кутів трикутника
рівна його сферичному надлишку з
оберненим знаком,
що служить контролем обчислення
![]() та
та
![]() .
Справді,
.
Справді,
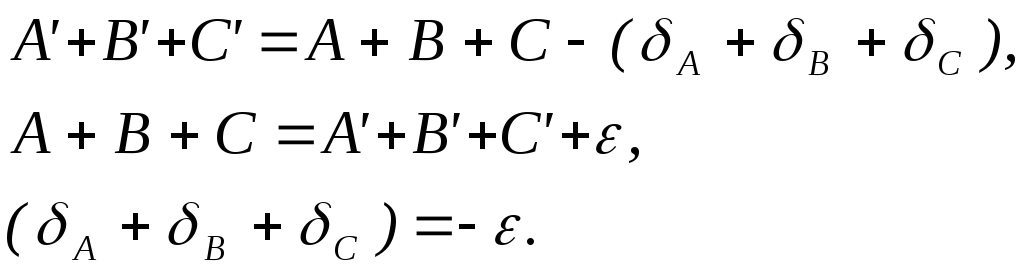
В тріангуляції 2-го класу для обчислення поправок за кривину зображення геодезичних ліній застосовують більш точні формули, які приведемо без доведення
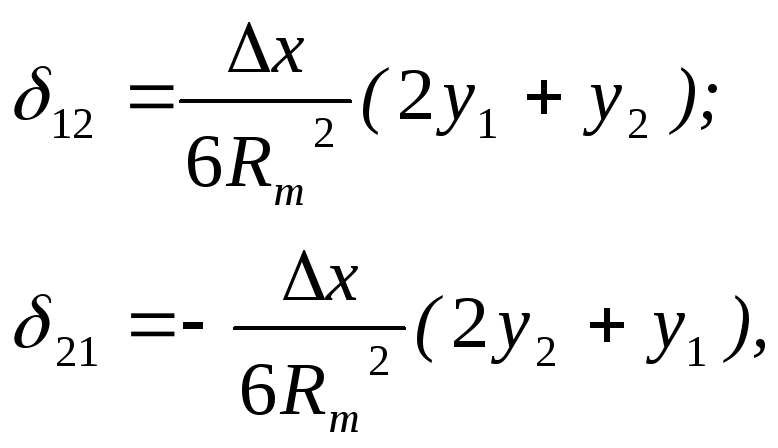 (4.32)
(4.32)
де
![]() - середній радіус кривини, обчислений
за широтою середньої точки заданої
геодезичної лінії.
- середній радіус кривини, обчислений
за широтою середньої точки заданої
геодезичної лінії.
Як
видно з наведених формул, для обчислення
редукцій повинні бути відомі плоскі
прямокутні координати початкового і
кінцевого пунктів. Визначимо необхідну
точність цих координат. Для цього
достатньо дослідити формулу (4.30).
Продиференціювавши дану формулу за
координатами
![]() і
і![]() ,
знаходимо
,
знаходимо
![]() .
.
Позначивши
![]() ,
отримаємо
,
отримаємо
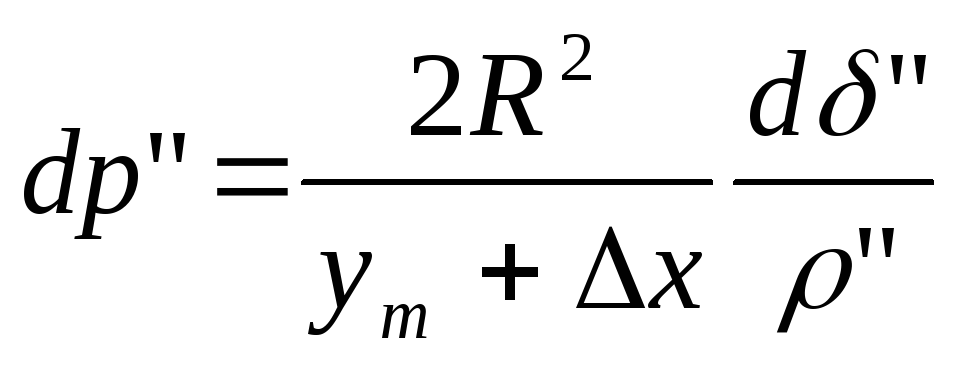 .
.
Нехай:
для тріангуляції 2-го класу
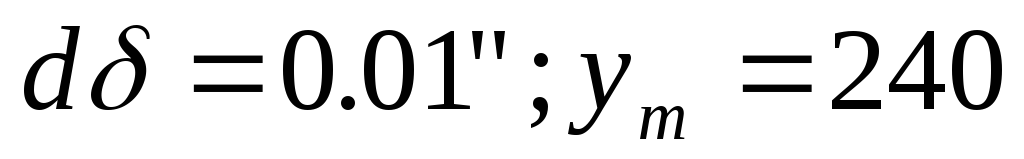 км
(на краю шестиградусної зони);
км
(на краю шестиградусної зони);
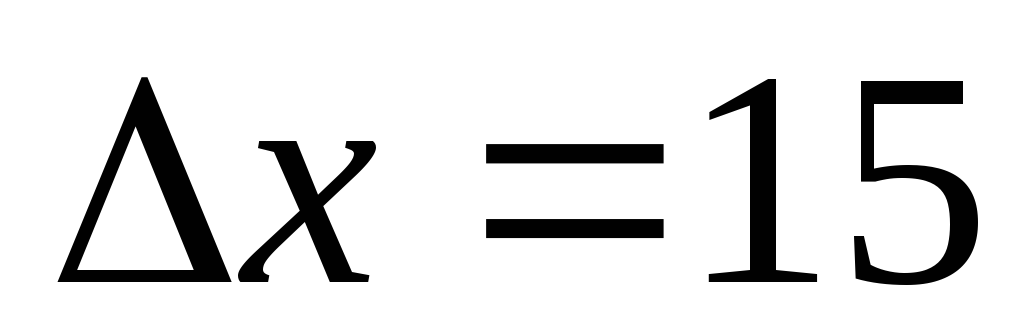 км,
тоді
км,
тоді
 м;
м;для тріангуляції 3-го класу
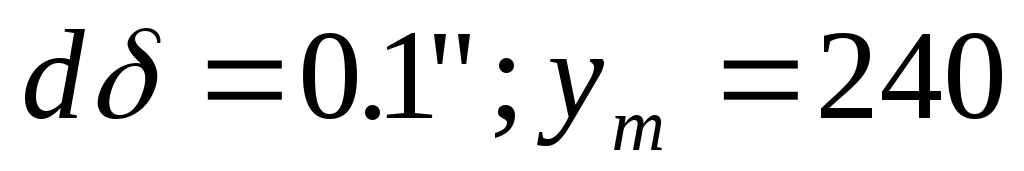 км;
км;
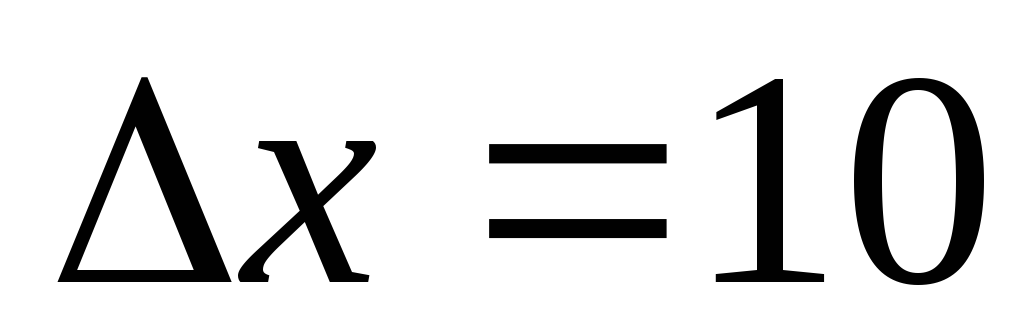 км,
тоді
км,
тоді
 м.
м.
Стосовно опрацювання кутомірних вимірювань нижчих класів (розрядів), то поправки за кривину (в межах шестиградусних зон) можна обчислювати за наближеною формулою:
![]() ,
,
а наближені координати пунктів можна вибрати із карти або схеми геодезичної мережі.
Нижче
наводиться таблиця абсолютних величин
поправок (редукцій) за кривину зображення
геодезичної лінії для різних значень
![]() та
та
![]()
Таблиця 4.1
-

 км
км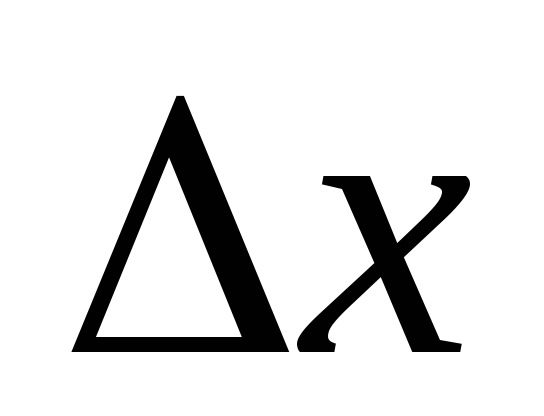 ,км
,км50
100
150
200
250
5
0.6”
1.2”
1.9”
2.5”
3.2”
10
1.3”
2.5”
3.8”
5.1”
6.4”
20
2.5”
5.0”
7.7”
10.1”
12.6”
Як
видно із таблиці 4.1, в знімальних мережах
(![]() км)
поправками за кривину, через їх незначні
величини, в порівнянні з похибками
вимірювання кутів, можна нехтувати.
км)
поправками за кривину, через їх незначні
величини, в порівнянні з похибками
вимірювання кутів, можна нехтувати.
Перед
виводом формул для редукцій відстаней
розглянемо спочатку питання про різницю
в довжинах зображення дуги геодезичної
лінії на площині
![]() та
хорди
та
хорди
![]() ,
шо стягує цю дугу.
,
шо стягує цю дугу.
Нехай
на рис.4.6
Згідно
таблиці 4.1, значення кута
Отже,
з похибкою на величину
![]() -
зображення дуги геодезичної лінії на
площині;
-
зображення дуги геодезичної лінії на
площині;
![]() - її хорда;
- її хорда;
![]() - кут між хордою і початковим елементом
дуги
- кут між хордою і початковим елементом
дуги
![]() .
Тоді можемо записати
.
Тоді можемо записати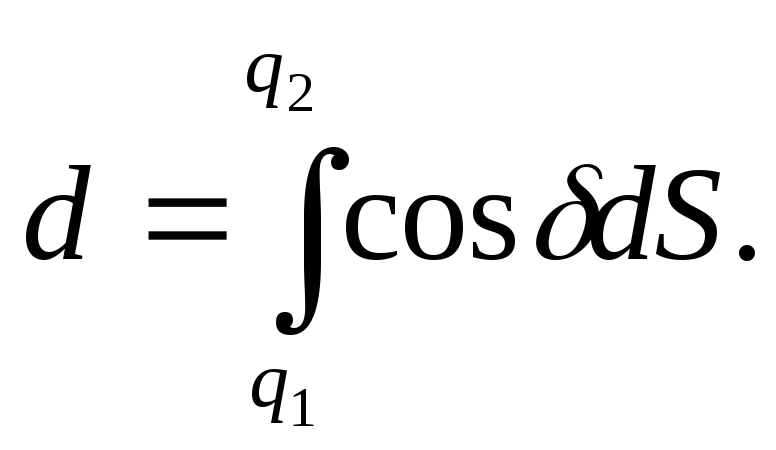
![]() при стандартних довжинах сторін
геодезичних мереж. Тому для малих кутів
можемо записати
при стандартних довжинах сторін
геодезичних мереж. Тому для малих кутів
можемо записати![]()
![]() можна прийняти, що
можна прийняти, що
![]() , тоді
, тоді
![]()

Рис.4.6
Із (4.12) можемо записати інтеграл
![]() ,
(4.33)
,
(4.33)
де
масштаб
![]() визначається формулою (4.29).
визначається формулою (4.29).
Знайти
інтеграл (4.33) в замкнутій формі надзвичайно
трудно, поскільки масштаб зображення
є досить складною функцією довжини
геодезичної лінії. Проте такі фактори
як порівняно невелика довжина геодезичної
лінії (<30
км)
і незначне віддалення від осьового
меридіану (![]() )
спрощують задачу знаходження інтегралу
(4.33), і її розв’язання
можна буде шукати наближеними методами.
)
спрощують задачу знаходження інтегралу
(4.33), і її розв’язання
можна буде шукати наближеними методами.
Одним із наближених методів обчислення вказаних означених інтегралів є чисельний метод. Конкретно для даного випадку можна застосувати формулу Сімпсона, розділивши інтервал інтегрування на дві частини. Тоді інтеграл (4.33) може бути представлений наступним наближенням
![]() (4.34)
(4.34)
де
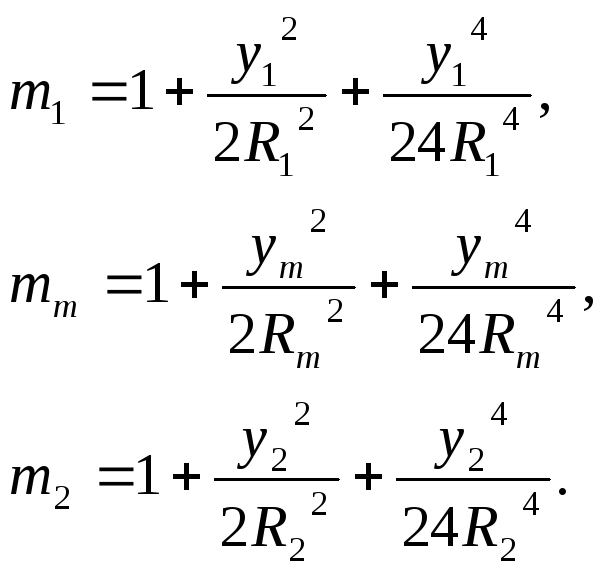 (4.35)
(4.35)
Якщо обчислення проводяться з геодезичними координатами, то для масштабів зображення можна використати формулу (4.27)
При
довжинах ліній, що не перевищують 30 км,
у всіх трьох виразах для масштабу
зображення радіус кривини
![]() можна обчислювати тільки для середньої
точки, а в членах четвертого порядку
прийняти
можна обчислювати тільки для середньої
точки, а в членах четвертого порядку
прийняти
![]() .
.
Для ординат можемо записати такі очевидні співвідношення
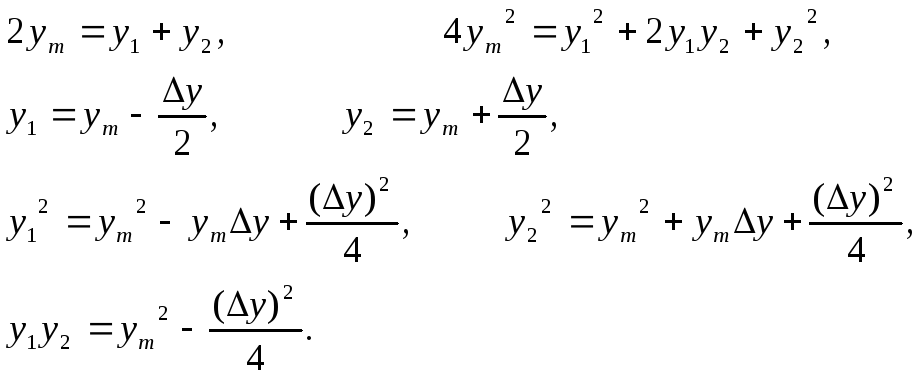
Підставивши в рівняння (4.34) вирази для масштабів (4.35) та використавши приведені вище співвідношення, отримаємо остаточну формулу
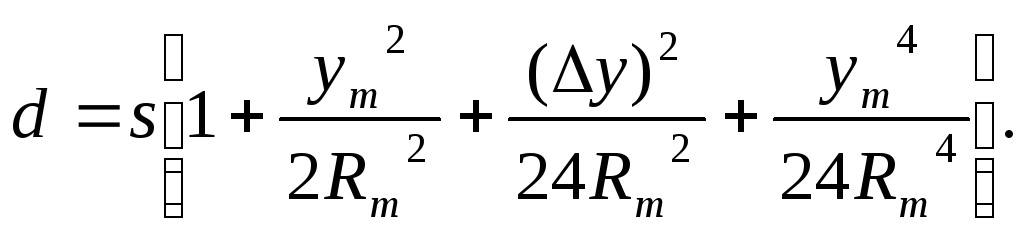 (4.36)
(4.36)
Із
отриманої формули видно, що лінія на
площині в проекції Гаусса-Крюгера завжди
довша від ліній, що зображуються з
еліпсоїда.
Третій і четвертий члени формули (4.36)
при
![]() км
(максимально можливі значення на краю
шестиградусної зони) і
км
(максимально можливі значення на краю
шестиградусної зони) і
![]() км складають 6 і 8 мм відповідно, тому в
роботах, де не вимагається висока
точність або коли розміри зони є меншими
(
км складають 6 і 8 мм відповідно, тому в
роботах, де не вимагається висока
точність або коли розміри зони є меншими
(![]() ),
можна користуватися формулою
),
можна користуватися формулою
![]() .
(4.36’)
.
(4.36’)
Підрахуємо
тепер, з якою похибкою допустимо знати
в (4.36) ординату
![]() середньої точки редукованої лінії.
середньої точки редукованої лінії.
При
похибці в
![]() ,
рівній
,
рівній![]() ,
отримаємо в
,
отримаємо в![]() похибку
похибку![]() ,
згідно (4.36’),
рівну
,
згідно (4.36’),
рівну
![]()
звідки
![]() .
.
Якщо
поставити вимогу, щоб
![]() не перевищувало 0.001 м, то, приймаючи
не перевищувало 0.001 м, то, приймаючи![]() км,
км,![]() км
і
км
і![]() км,
отримаємо, що
км,
отримаємо, що![]() м.
м.
Практика застосування проекції Гаусса-Крюгера.
Областю
зображення або областю розповсюдження
системи плоских прямокутних координат
є к о о р д и н а т н а з о н а, обмежена
двома меридіанами, з різницею довгот в
![]() ,
переважно в 6о
- шестиградусна зона. Номерація зон, а
відповідно і довгота осьового меридіана,
пов’язана
з прийнятою номенклатурою карт. Кожна
шестиградусна зона відповідає одній
колоні листів карти масштабу 1:1 000 000 і,
якщо N
є номером колони, то номер шестиградусної
зони n
визначається
за формулою
,
переважно в 6о
- шестиградусна зона. Номерація зон, а
відповідно і довгота осьового меридіана,
пов’язана
з прийнятою номенклатурою карт. Кожна
шестиградусна зона відповідає одній
колоні листів карти масштабу 1:1 000 000 і,
якщо N
є номером колони, то номер шестиградусної
зони n
визначається
за формулою
![]() .
.
Осьовий
меридіан шестиградусної зони проекції
Гаусса-Крюгера збігається із середнім
меридіаном відповідної колони карти
масштабу 1:1 000 000. Звідси виходить, що
довгота осьового меридіана може бути
знайдена за формулою
![]() .
Довгота межового меридіана шестиградусної
зони відносно осьового рівна
.
Довгота межового меридіана шестиградусної
зони відносно осьового рівна
![]() .
.
В топографічних роботах крупного масштабу застосовуються триградусні зони, а в спеціальних роботах можуть і ще вужчі, але при цьому координати опорних пунктів даються і в шестиградусній зоні.
Прямолінійне зображення осьового меридіана і екватора, які приймаються за осі декартових координат, дозволяють створити в кожній координатній зоні самостійну систему плоских координат, яка використовується у всіх видах геодезичних і топографічних робіт, що виконуються в межах однієї зони.
Системи
координат в кожній зоні проекції
Гаусса-Крюгера абсолютно ідентичні:
плоскі координати x
і
y,
обчислені за геодезичними координатами
![]() в будь-якій координатній зоні, мають
одні і ті ж значення.
в будь-якій координатній зоні, мають
одні і ті ж значення.
Для однотипного способу аналітично виражати положення будь-якої точки земної поверхні Баумгарт (1919) вніс пропозиції:
оптимальним вважати поділ на триградусні зони;
виключити з вжитку від’ємні ординати шляхом додавання до них 500 000 м;
за осьові меридіани прийняти меридіани 3, 6, 9, 12о, … східної довготи, відносячи їх до Грінвіча, а перед ординатою вказувати відповідні їм номери
