3.10. Порядок построения диаграммы

1. Построение векторных диаграмм начинаем с выбора масштаба для тока и напряжения. .

m_I = 1 А/ см, m_U = 5 B/ см. Здесь и масштабные коэффициенты. ОНи означают, сколько ампер или вольт содержится в 1 см. Масштаб можно задавать и графически, смотри рисунок.

От точки 0 горизонтально вправо проводим вектор тока I общий для всей цепи. В выбранном масштабе его длина будет l_I = I / m_I = 2 А / (1 А / см)= 2 см

2. Вектор активного напряжения U_R1 совпадает по фазе с током, угол сдвига фаз между ними равен 0, поэтому откладываем его вдоль вектора тока от точки 0 вправо.

Его длина l_UR1 = U_R1 / m_U =18 В / (5 В / см)=3,6 см

3. От конца вектра U_R1 откладываем вправо вдоль вектора тока вектор активного напряжения U_R2. Его длина l_UR2 = U_R2 / m_U= 22 В / (5 В / см) = 4,4 см

4. От конца вектора U_R2 откладывае вертикально вверх вектор падения напряжения U_L на индуктивном сопротивлении, так как он опережает ток на угол 90.

Его длина l_{U L} = U_L / m_U = 24 см / (5 В/см) = 4, 8 см.

5. От конца вектора U_L откладываем вертикально вниз вектор падения напряжения U_C на емкостном сопротивлении, так как он отстает от тока на угол 90º.

Его длина l_UC = / m_U =54 В / (5 В/см) = 10, 8 см.

Геометрическая сумма векторов U_R1, U_R2, U_L, U_C должна быть равна полному напряжению U, приложенному к зажимам цепи, т. е. U = U_R1+ U_R2+ U_L +U_C

Измерив длину этого вектора, убеждаемся, что она l_U = 10 см. Это значит, что с учетом масштаба его величина будет U = 10 см. ∙ 5 В/ см = 50 В.

По условию задачи именно такое напряжения приложено к зажимом цепи.

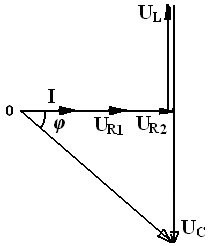
Примечание. Если в выбранном масштабе вектор суммарного напряжения не будет равен приложенному к зажимам цепи напряжения, то это будет означать об ошибке, допущенной при решении задачи или в построении векторной диаграммы. Ее нужно найти и устранить. Чаще всего наблюдаются ошибки, связанные с искажением масштабов при построении векторной диаграммы. Учтите это, и при построении вектоной диаграммы пользуйтесь чертежным инструментом. Выполняйте постоение точно и аккуратно.

3.11. Расчет параллельных цепей переменного тока

Методика (с примером) решения задач на тему: Электрические цепи с параллельным соединением активного, емкостного и индуктивного сопротивлений

Цель. Рассчитать напряжения, токи на элементах цепи. Построить диаграмму напряжений и токов.

Теория к работе.

Для такой цепи характерно, что электроприемники, соединенные параллельно, находятся под одинаковым (общим) напряжением. (При отсутствии на параллельных цепях какого-либо элемента вместо них в формулах будет стоять, естественно, нуль!).

Ток каждой ветви определяется по закону Ома:

I₁ = U /Z₁, где Z₁ = ,

I₂ = U /Z₂, где Z₂ =

Углы сдвига фаз φ₁ и φ₂ между током и напряжением каждой ветви определяются с помощью тригонометрических функций:

cos φ₁= R₁ / Z₁ и sin φ₁= X_L1 / Z₁,

cos φ₂= R₂ / Z₂ и sin φ₂= - X_C2 / Z₂

Угол сдвига фаз обязательно следует проверять по синусу во избежание потери знака угла (cos является четной функцией), но находить его тоже нужно. Он потребуется в дальнейшем расчете цепи.

Общий ток цепи следует из I закона Кирхгофа, он равен векторной сумме токов ветвей: I = I₁ + I₂

Векторная диаграмма этих токов:

Общий суммарный или результирующий ток можно найти не только графически (диаграмма строится в масштабе), но и математически, на основании теоремы Пифагора:

I = ,

где Iа – проекция вектора общего тока на вектор напряжений, она называется активной составляющей общего тока.

Iр – проекция вектора общего тока на линию, перепндикулярную линии напряжения, она называется реактивной составляющей общего тока.

Из диаграммы видно, что Iа = Iа₁ + Iа₂ , Iр = I_L1  Iс₂

В этих формулах: Iа₁ и Iа₂ - активные составляющие токов первой и второй ветви.

I_L1 - реактивные составляющие тока первой ветви. Она носит индуктивный характер и поэтому взята знаком “плюс”.

Iс₂ - реактивные составляющие тока второй ветви. Она носит емкостной характер и поэтому взята знаком “минус”.

Введем в формулу общего тока его составляющие, тогда

I =

Значения составляющих токов ветвей можно определять по формулам:

Iа₁ = I₁ cos φ₁; Iа₂ = I₂ cos φ₂; I_L1 = I₁ sin φ₁; I_C2 = I₂ sin φ₂ ;

Активная мощность цепи равна арифметической сумме активных мощностей ветвей:

Р = Р₁ + Р₂, где Р₁ = U I₁ cos φ₁ или Р₁ = I₁²R₁,

Р₂ = U I₂ cos φ₂ или Р₂ = I₂²R₂

Реактивная мщность цепи равна алгебраической сумме реактивных мощностей ветвей:

Q =Q_L1 – Q_{C2 ,} где

Q_L1= U I₁ sin φ₁ или Q_L1=I₁² Х L₁,

Q _C2= U I₂ sin φ₂ или Q_С2=I₂² Х _С2

Активную и реактивную мощность можно найти и так: Р = U I cos φ или Q= U I sin φ

Где

cos φ = ,

sin φ=

cos φ и sin φ используют также для определения угла сдвига фаз между общим током и напряжением.

Полная мощность цепи:

S =U I или S =

Угол сдвига фаз между общим токомм и напряжением можно определять и из выражений:

cos φ = Р / S, sin φ = Q/ S