
- •Часть 1. Тема «Законы постоянного тока» 10
- •Часть 2. Электромагнетизм 27
- •Часть 3. Переменный ток (краткая теория) 44
- •Часть 4. Трехфазный ток 76
- •Часть 5. Трансформаторы 98
- •Часть 6. Электрические машины 128
- •Часть 7. Практическая работа: Расчет стоимости электроэнергии 174
- •Указания к выполнению и оформлению контрольных работ
- •Выбор вариантов задач контрольной работы
- •Содержание учебной дисциплины
- •Раздел 1 Электрическое поле. Электрические цепи постоянного тока
- •Раздел 2. Электромагнетизм и электромагнитная индукция
- •Раздел 3. Электрические измерения и электротехнические приборы
- •Раздел 4. Электрические цепи переменного однофазного тока
- •Раздел 5. Трехфазные электрические цепи
- •Раздел 6. Трансформаторы
- •Раздел 7. Электрические машины переменного и постоянного тока
- •Раздел 8. Основы электроники. Полупроводниковые приборы
- •1.1 Закон Ома для участка и полной цепи
- •1.2. Последовательное и параллельное соединение проводников
- •Последовательное соединение
- •Общее напряжение u на проводниках равно сумме напряжений u1, u2 ,u3 равно:
- •Параллельное соединение
- •1.3. Расчет сложных цепей. Правила Кирхгофа
- •1.4. Пример на запись уравнений по законам Кирхгофа
- •1.5. Уравнение баланса мощностей
- •1.6. Расширение пределов измерения амперметра и вольтметра
- •1.7. Примеры решения задач
- •1.7.1. Пример 1
- •1.7.2. Пример 2
- •1.7.3. Пример 3
- •1.5. Задания к контрольной работе Задачи вариантов 1 – 10, 11 – 20, 21-30
- •Задачи вариантов 31- 40, 41 – 50
- •Часть 2. Электромагнетизм
- •2.1. Основные формулы и уравнения
- •Взаимодействие проводников с током. Электромагнит.
- •Напряженность магнитного поля. Магнитное напряжение.
- •Закон полного тока.
- •Индуктивность
- •Энергия магнитного поля
- •Взаимная индукция
- •2.2. Вопросы по теме «Магнитные свойства вещества»
- •1 Вариант
- •2 Вариант
- •3 Вариант
- •2.3. Характеристики намагничивания стали
- •2.4. Расчет магнитной цепи
- •Теоретическая часть
- •2.5. Задача на расчет магнитной цепи Задача 1. Прямая задача расчета мц
- •Порядок расчета.
- •Задача 2. (обратная задача расчета мц)
- •2.6. Задания вариантам практической работе «Расчет магнитных цепей»
- •Часть 3. Переменный ток (краткая теория)
- •3.1. Получение синусоидальной эдс
- •3.2. Характеристики синусоидальных величин
- •3.3. Цепь переменного тока с активным сопротивлением
- •3.4. Цепь с катушкой индуктивности
- •3.5. Цепь с конденсатором
- •3.6. Основные формулы и уравнения
- •3.7. Задачи с решениями по теме
- •3.8. Методические указания к решению задач
- •Общее решение типовых задач
- •3.9. Примеры задачи при последовательном соединении Особенности расчета цепи при другой комбинации элементов схемы
- •3.10. Порядок построения диаграммы
- •3.11. Расчет параллельных цепей переменного тока
- •3.12. Пример задачи параллельного соединения
- •Решение.
- •Построение векторной диаграммы
- •3.13. Практическая работа
- •3.14. Задания по теме «Синусоидальный переменный ток» Задачи вариантов 1 -10
- •Задачи вариантов 11-20
- •3Адачи вариантам 21 – 30
- •Задачи вариантам 31- 40
- •Задачи вариантов 41 – 50
- •Часть 4. Трехфазный ток
- •4.1. Трехфазный ток (краткая теория)
- •4.1.1. Трехфазные системы
- •4.1.2. Схемы соединения трехфазных систем
- •Соединение обмоток генератора звездой
- •2. Соотношение между линейными и фазными напряжениями при соединении обмоток генератора звездой
- •3. Соединение обмоток генератора треугольником
- •4. Соединение приемников энергии звездой
- •4.2. Методические указания по теме «Трехфазные электрические цепи»
- •4.3. Пример решения задачи по схеме «звезда»
- •4.4. Пример решения задачи по схеме «треугольник»
- •Решение.
- •Порядок построения векторной диаграммы
- •4.5. Задания контрольной работе Задачи вариантов 1 -10
- •Задачи вариантов 11 – 20
- •Задачи вариантов 21 – 30
- •Задачи вариантов 31 – 40
- •Задачи вариантов 41 – 50
- •Часть 5. Трансформаторы
- •5.1. Устройство, назначение, принцип работы, применение
- •5.1. 1. Назначение и применение
- •5.1.2. Устройство трансформатора
- •5.1. 3. Нагрев и охлаждение трансформаторов
- •5.1.4. Формула трансформаторной эдс
- •5.1.5. Принцип действия. Коэффициент трансформации
- •5.1.6. Холостой ход однофазного трансформатора
- •5.1.7. Работа нагруженного трансформатора и диаграмма магнитодвижущих сил
- •5.1.8. Изменение напряжения трансформатора при нагрузке
- •5.1.9. Мощность потерь в обмотках нагруженного трансформатора
- •5.1.10. Трехфазные трансформаторы
- •5.1.11. Регулирование напряжения трансформаторов
- •5.1.12. Автотрансформаторы
- •5.1.13. Измерительные трансформаторы
- •5.1.14. Сварочные трансформаторы
- •5.2. Расчет трансформатора
- •5.2.1. Номинальные значения
- •5.2.2. Пример по схеме «звезда» (однофазный трансформатор)
- •5.2. 3. Пример задачи трехфазного трансформатора
- •5.3. Задания контрольной работе Задачи вариантов 1 – 10 (однофазный понижающий трансформатор)
- •Задачи вариантам 11-20
- •Технические данные трансформатора
- •Часть 6. Электрические машины
- •6.1. Электрические машины переменного тока (теория)
- •6.1.1. Назначение и их классификация.
- •6.1.2. Вращающееся магнитное поле
- •2. Подключить к катушкам несовпадающие по фазе токи.
- •6.1.3. Устройство трехфазных асинхронных двигателей
- •6.1.4. Принцип действия асинхронного двигателя
- •6.1.5. Регулирование частоты вращения асинхронных двигателей
- •6.1.6. Однофазные асинхронные двигатели
- •1. Однофазный двигатель не имеет пускового момента. Он будет вращаться в ту сторону, в которую раскручен внешней силой.
- •6.1.7. Принцип действия асинхронного и синхронного двигателей
- •6.2. Электрические машины постоянного тока
- •6.2.1. Устройство машин постоянного тока
- •6.2.2. Принцип действия машины постоянного тока
- •6.2.3. Электродвижущая сила якоря и электромагнитный момент
- •6.2.4. Генераторы постоянного тока
- •6.2.5. Двигатель постоянного тока с параллельным возбуждением
- •6.2.6. Общие сведения о двигателях с последовательным и смешанным возбуждением
- •6.2.7. Коллекторные двигатели переменного тока
- •6.2.7. Синхронные двигатели. Конструкция, принцип действия
- •6.3. Методические указания и задачи
- •6.3.1. Расчет генератора постоянного тока
- •Решение
- •6.3.2. Расчет двигателя постоянного тока
- •Решение
- •6.3. 3. Расчет двигателей переменного тока
- •Пример расчета двигателя
- •Решение
- •6.3.4. Расчет трехфазного асинхронного двигателя с короткозамкнутым ротором
- •6.4. Задания контрольных работ Задачи вариантов 1 - 10
- •Задачи вариантов 11 - 20
- •Задачи вариантам 21 - 30
- •Часть 7. Практическая работа: Расчет стоимости электроэнергии
- •Часть 8. Электробезопасность
- •8.1. Защитное заземление и зануление на строительных площадках
- •Возможные прикосновения
- •2. Режим нейтрали трансформатора
- •3. Трехфазная трехпроводная сеть с изолированной нейтралью
- •4. Защитное заземление и зануление
- •5. Защитное зануление
- •Первое требование
- •Второе требование
- •8.2. Общие требования к заземляющим устройствам
- •Естественные и искусственные заземлители
- •8.3. Заземление и зануление передвижных установок и переносных электроинструментов
- •8.4. Правила эксплуатации защитного заземления и зануления
- •Часть 9. Практическая работа. Тема. Выбор типа электродвигателя
- •2. Режимы работы
- •3.Выбор двигателей для различных режимов работы
- •3.1.Продолжительный режим работы
- •3.2.Повторно-кратковременный режим работы
- •3.3. Кратковременный режим работы
- •1.4. Определить моменты двигателя
- •2.3. Определяется расчетная продолжительность включения:
- •Задания контрольной работы
- •Технические данные асинхронных двигателей основного исполнения
- •Часть 10. Экзаменационные вопросы по электротехнике
- •10.1. Критерии оценивания
- •10.2. Экзаменационные вопросы
- •Литература
3.5. Цепь с конденсатором
На практике, т. е. в силовых цепях, конденсатор рассматривают как элемент цепи, не имеющий потерь. Заряд конденсатора q пропорционален напряжению между его обкладками
q
= CU.
Условное обозначение
емкости изображено на рис.3.7, б.
Скорость изменения
заряда q
равна электрическому
току, тогда i
=
![]() =
C
=
C![]() (3.18)
(3.18)
Таким образом, сила тока в цепи с конденсатором пропорциональна скорости изменения напряжения на его обкладках.
Выясним, как будет изменяться сила тока, если к конденсатору приложить напряжение, изменяющееся по синусоидальному закону и = Um sin ωt (pиc. 3 6. a)
Ток в цепи
i
=
![]() =
C
=
C![]() =C
=C![]() =ωCUm
cosωt,
т. е. i
= Im
sin(ωt+90°)(3.19)
=ωCUm
cosωt,
т. е. i
= Im
sin(ωt+90°)(3.19)
Величина ωCUm = Im есть амплитуда тока.
Действующее значение тока
I
= ω
CU=![]() =
=![]() (3.20)
(3.20)
Величину
ХC=
![]() =
=![]() (3.21)
(3.21)
имеющую размерность сопротивления [XC] = с • В/Кл = В • с / А • с = Ом, называют емкостным сопротивлением.
Для получения XC в омах нужно емкость выражать в фарадах. Емкостное сопротивление обратно пропорционально частоте тока и емкости конденсатора (цепи). Суть емкостного сопротивления можно продемонстрировать, если в схеме цепи с индуктивным сопротивлением трансформатор заменить батареей конденсаторов. Изменяя емкость батареи конденсаторов, заметим усиление или ослабление накала лампы.
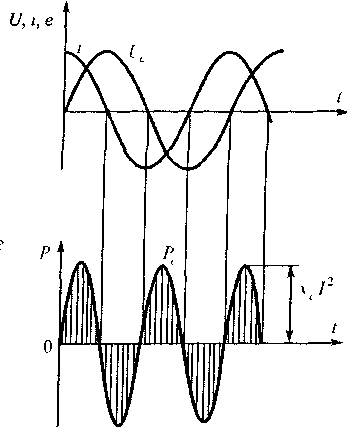
Рис. 3.7. График мгновенной мощности в цепи переменного токапри емкостном сопротивлении: а - цепь;
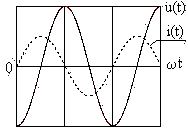
б- условное обозначениеемкостного элемента; в— графики мгновенного значения тока и напряжения;
г - график мгновенной мощности; д - векторная диаграмма тока и напряжения
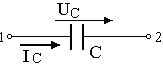 a)
a)
![]() б)
б)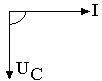 д)
д)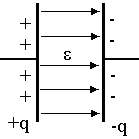 е)
е)
Сопоставление уравнений напряжения и тока показывает, что в цепи с емкостью напряжение отстает от тока по фазе на 90° (рис.3.7, в).
Мгновенное значение мощности в цепи с емкостью определяется как p = u i и строится точно так же, как и для цепи с индуктивностью.
Из графика (рис.3.7,г)
видно, что мощность
меняет свой знак каждые четверть
периода. Сначала энергия накапливается
на емкости, когда напряжение растет;
в этот момент конденсатор является
приемником энергии WC
=
![]()
Затем, когда напряжение уменьшается, конденсатор разряжается и энергия возвращается источнику, т. е. конденсатор является источником энергии.
Таким образом, активная мощность цепи с емкостью равна нулю (Р= 0), а реактивная мощность Q- произведению действующих значений напряжения и тока: Q=UcI −XC I2 (3.22)
Векторная диаграмма напряжения и тока приведена на рис. 3.7, д.
В цепи с емкостью, так же как и в цепи с индуктивностью, преобразование электрической энергии в другие виды энергии, кроме как в энергию электрического поля, не происходит.
3.6. Основные формулы и уравнения
Переменный электрический ток (ЭДС, напряжение)— это ток (ЭДС, напряжение), изменяющийся с течением времени. Значение этой величины в рассматриваемый момент времени называется мгновенным значением тока (ЭДС, напряжения).
Переменный синусоидальный ток (ЭДС, напряжение) – это ток, являющийся синусоидальной функцией времени. Переменный ток характеризуется периодом Т, (с), и величиной, обратной периоду - частотой электрического тока (ЭДС, напряжения) f, (Гц):
f
=![]() ;
(3.23)или f
=
;
(3.23)или f
=![]() ,
(3.24)
,
(3.24)
где р — число пар полюсов генератора; п — частота вращения якоря генератора, об/мин.
Мгновенные значения тока, ЭДС, напряжения соответственно:
i = Im sin (ωt ± Ψi),
e = Em sin (ωt ± Ψe), (3.25)
и = Um sin (ωt ± Ψu),
где i, е, и — мгновенные значения тока, А; ЭДС, В; напряжения, В;
Im, Em, Um — амплитудные значения тока, А; ЭДС, В; напряжения, В;
ω — угловая частота, 1/с; Ψi , Ψe , Ψu — начальная фаза тока, ЭДС, напряжения; t— время, с.
Угловая частота синусоидального электрического тока (ЭДС, напряжения) ω=2лf. (2.4)
Начальная фаза тока (ЭДС, напряжения) (Ψi, Ψe, Ψu) — значение фазы в момент времени t= 0.
Разность начальных фаз двух синусоидальных величин одной и той же частоты называют сдвигом фаз. Сдвиг фаз между напряжением и током определяется вычитанием начальной фазы тока из начальной фазы напряжения: φ = Ψu - Ψi (3.26)
Синусоидально изменяющиеся величины изображают графически как функции времени t (угла ωt), и вращающимися векторами на плоскости. В последнем случае длина вектора в выбранном масштабе представляет собой амплитудное или действующее значение этой величины, угол между этим вектором и положительным направлением оси абсцисс в начальный момент времени равен начальной фазе Ψ, а угловая частота вращения вектора равна угловой частоте ω.
Совокупность двух и большего числа векторов называют векторной диаграммой. Сложение векторов производят по правилу параллелограмма. Вычитание их — сложение с обратной по знаку вычитаемой величиной.
Действующее значение переменного тока (ЭДС, напряжения) — это среднеквадратичное значение переменного тока (ЭДС, напряжения) за период Т:
I
=
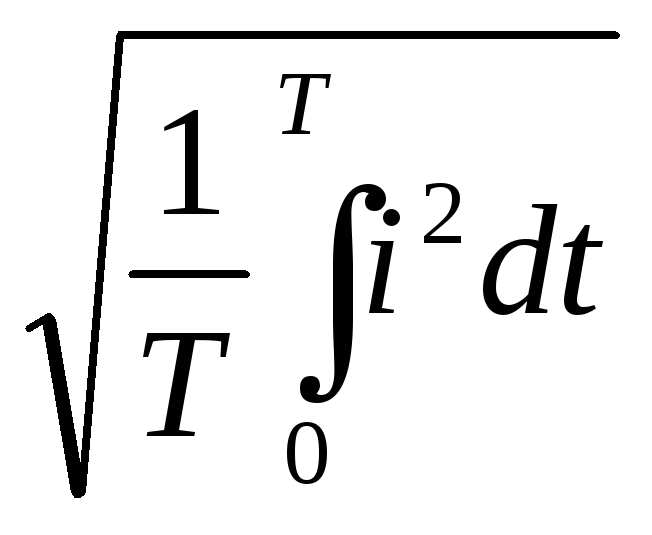 (3.27)
(3.27)
I
=
![]() = 0,7074 Im
E
=
= 0,7074 Im
E
=
![]() = 0,7074 Em
U
=
= 0,7074 Em
U
=![]() = 0,7074 Um
= 0,7074 Um
Если ток, ЭДС или напряжение изменяются по синусоидальному закону, то его действующее значение составляет 0,707 амплитудного значения:Так как действующие значения токов, ЭДС и напряжений пропорциональны амплитудам этих величин, то вектор, выражающий в одном масштабе амплитудное значение, в другом представляет собой действующее значение той же величины. Чаще векторные диаграммы строят в действующих значениях.
