
- •1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
- •1.2. Правило вычисления определителя любого порядка
- •1.4. Математические операции над матрицами
- •1.5. Понятие системы линейных алгебраических уравнений
- •1.6. Решение систем линейных алгебраических уравнений
- •2. ВЕКТОРНАЯ АЛГЕБРА
- •2.3. Линейные операции над векторами
- •2.6. Векторное произведение векторов
- •2.7. Понятие смешанного произведения векторов
- •3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
- •3.1. Линия на плоскости
- •3.2.4. Прямая, проходящая через две заданные точки
- •3.2.7. Расстояние от точки до прямой
- •3.2.8. Деление отрезка в данном отношении λ
- •3.3. Кривые второго порядка
- •3.3.1. Окружность
- •3.3.2. Эллипс
- •3.3.3. Гипербола
- •3.3.4. Парабола
- •3.3.5. Общее уравнение кривой второго порядка
- •3.4. Плоскость в пространстве
- •3.4.1. Общее уравнение плоскости
- •3.4.2. Неполные уравнения плоскости
- •3.4.5. Взаимное расположение двух плоскостей в пространстве
- •3.5.2. Канонические уравнения прямой
- •3.5.3. Параметрические уравнения прямой
- •3.5.6. Взаимное расположение прямой и плоскости
- •4. МАТЕМАТИЧЕСКИЙ АНАЛИЗ
- •4.1. Основные понятия
- •4.2. Классификация основных элементарных функций
- •4.3. Предел функции
- •4.6. Основные свойства конечных пределов
- •4.7. Вычисление пределов
- •4.8.4. Свойства функции, непрерывной на отрезке
- •4.9.7. Правило Лопиталя
- •4.10.2. Интервалы монотонности функции. Точки экстремума
- •4.10.5. Четность, нечетность и периодичность функции
- •4.10.6. Нули функции и дополнительные точки
- •Вопросы для самопроверки
Смешанное произведение обозначается |
|
|
|
|
|
|
|
|
||||||
a |
b c |
или a b c . |
|
|
|
|||||||||
|
|
|
|
|
k |
|
|
|
|
|
ax |
ay |
az |
|
|
|
|
i |
j |
|
|
|
|
|
|
||||
ax |
ay |
az |
|
bx |
by |
bz |
. |
|||||||
a b |
c |
cxi cy j czk |
||||||||||||
|
|
|
bx |
by |
bz |
|
|
|
|
|
cx |
cy |
cz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, если векторы a,b,c |
компланарны, то a |
b c 0 . |
||||||||||||
Вопросы для самопроверки
1)Что называется скалярной и векторной величиной?
2)Дайте определение коллинеарных, компланарных, равных векторов.
3)Что называется углом между векторами?
4)Как найти длину вектора, заданного двумя точками?
5)Дайте определение базиса на плоскости и в пространстве.
6)Какие операции над векторами называются линейными?
7)Что называется скалярным произведением векторов?
8)Приведите формулу скалярного произведения в координатах.
9)Каков физический смысл скалярного произведения?
10)Какая тройка векторов называется левой, а какая – правой?
11)Дайте определение векторного произведения, приведите его формулу и свойства.
12)Каков физический смысл векторного произведения?
13)Приведите понятие смешанного произведения.
Литература: [1], c.4-7, 20-39 Примеры: [2], c.44-52
3.АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
3.1.Линия на плоскости
Любую линию на плоскости ХОY будем рассматривать как множество точек, обладающих некоторым геометрическим свойством – геометрическое место точек
(ГМТ).
Обозначим: т.М(х,у) – произвольная или текущая точка линии; х,у - текущие координаты; т.М0(х0,у0) – фиксированная точка линии.
Определение. Уравнение F x,y 0 называется уравнением линии L, если координаты каждой точки линии удовлетворяют этому уравнению, и наоборот, если координаты какой-либо точки удовлетворяют этому уравнению, то данная точка принадлежит линии L.
Пример. Составить уравнение окружности с центром в т.С(α,β) и радиуса R. Определение . Окружность – ГМТ плоскости, равноудаленных на расстояние
R от фиксированной точки плоскости, называемой центром.
Пусть т.М(х,у) – текущая точка окружности и т.С (α,β) – центр окружности. Геометрическое свойство окружности: CM R или
23


 xM xC 2 yM yC 2 R ;
xM xC 2 yM yC 2 R ; 
 x 2 y 2 R . Таким образом, уравнение смещенной окружности с центром в т.С (α,β) и радиуса R: x 2 y 2 R2 .
x 2 y 2 R . Таким образом, уравнение смещенной окружности с центром в т.С (α,β) и радиуса R: x 2 y 2 R2 .
Если 0, 0 , то центр окружности лежит в т.О(0,0) и уравнение имеет вид: x2 y2 R2 . Такое уравнение называется каноническим уравнением окруж-
ности.
Определение. Линия L называется алгебраической линией n-го порядка, если уравнение линии F(x,y) = 0 является многочленом n-го порядка относительно переменных х, у.
Примеры: x2 y2 R2 – линия 2-го порядка;
2x y 2 – линия 1-го порядка; y x3 – линия 3-го порядка.
Линия L, не являющаяся алгебраической, называется трансцендентной.
Примеры: y sin x, y cos x, y ln x, y ex .
3.2. Прямая линия на плоскости 3.2.1. Общее уравнение прямой
Определение. Любой вектор n A;B , перпендикулярный прямой линии L,
называется ее нормалью.
Прямая линия имеет бесконечно много векторов нормали, они коллинеар-
ны.
Пусть вектор M0 M расположен на линии L и вектор n L . Тогда их скалярное произведение равно нулю:
|
имеет координаты A;B , |
n M0M 0 , где вектор n |
|
вектор M0M - координаты |
x x0 ,y y0 (рис.3.1). |
Тогда: A x x0 B y y0 0 |
или Ax By Ax0 By0 0; |
обозначим C Ax0 By0 . |
|
y 
M x,y n A;B
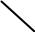 M0 x0 ,y0
M0 x0 ,y0
0 |
x |
L
Рис. 3.1
Уравнение прямой L вида Ax By C 0 называется общим уравнением
прямой на плоскости.
Геометрический смысл коэффициентов А, В при неизвестных: А, В - координаты вектора нормали n данной прямой.
|
Неполные уравнения прямой: |
||
1) |
C 0, |
Ax By 0 – прямая проходит через т.О(0,0). |
|
2) |
A 0; |
By C 0; y C |
– прямая параллельна оси ОХ (горизонталь). |
|
|
B |
|
3) |
B 0; |
Ax C 0; x C |
– прямая параллельна оси ОY (вертикаль). |
|
|
A |
|
24

4)А = 0; С = 0; Ву = 0, у = 0 – ось ОХ.
5)В = 0; С = 0; Ах = 0; х = 0 – ось ОY.
3.2.2. Прямая с угловым коэффициентом
Определение . Угловым коэффициентом k прямой Lназывается тангенс угла наклона φ прямой к оси ОХ, k tg (рис.3.2).
Определение . Любой вектор а , параллельный прямой L или расположенный на ней, называется направляющим вектором прямой.
Прямая имеет бесконечно много направляющих векторов, они коллинеарны.
|
|
a |
y |
|
|
a |
y |
|
|
|
|
Рассмотрим рис. 3.3: a ax , ,ay ; tg k ; |
tg |
|
; |
k |
|
. |
|
|
|
||
|
|
|
|
|
|
|
|||||
|
|
ax |
|
ax |
|
|
|
||||
Возьмем на линии L две точки: В(0, b) |
и М(х,у) (рис. 3.4), при этом вектор |
||||||||||
BM x; y b – направляющий вектор прямой |
|
L. |
Тогда |
k |
y b |
, отсюда |
|||||
|
x |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y kx b – уравнение прямой с угловым коэффициентом. Геометрический смысл:
k tg , |
φ – угол наклона прямой к оси ОХ; b – отрезок, отсекаемой прямой по |
оси ОY. |
|
Рис. 3.2 |
Рис. 3.3 |
Рис. 3.4 |
3.2.3.Прямая, проходящая через заданную точку М0(х0, у0)
с заданным угловым коэффициентом k (пучок прямых)
Пусть т. M0 x0 , y0 L , тогда ее координаты удовлетворяют уравнению пря-
мой: y0 kx0 b . Вычтем из уравнения y kx b полученное уравнение, в ре-
зультате получим: y y0 k x x0 . Это уравнение и называется уравнением пуч-
ка прямых с центром в т. M0 x0 , y0 .
3.2.4.Прямая, проходящая через две заданные точки
|
|
Пусть точки на прямой L имеют координаты: |
|
|
|
|
|
M L |
||||||
|
|
|
|
|
т.М1(х1, у1), т.М2(х2, у2), |
т.М(х, у) (рис.3.5). |
|
|
|
|||||
Вектор M M x x ;y y коллинеарен вектору MM |
x x ;y y , |
M2 |
||||||||||||
M1 |
||||||||||||||
|
|
|
1 |
1 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
|
||
поэтому их одноименные координаты пропорциональны: |
|
|
|
|||||||||||
|
x x1 |
|
y y1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
. Эта формула называется уравнением прямой, |
|
Рис. 3.5 |
|||||||
|
x |
x |
y |
y |
|
|||||||||
2 |
1 |
2 |
1 |
|
|
|
|
|
|
|
|
|
||
проходящей через две заданные точки.
Следствия.
1. Вектор M1M2 x2 x1; y2 y1 является направляющим вектором прямой.
25

2. Если известен направляющий вектор прямой |
|
ax , |
,ay |
и точка M1 x1 ,y1 L , |
||||
a |
||||||||
то ее уравнение можно записать в виде: |
x x1 |
|
y y1 |
. |
|
|
||
|
|
|
|
|||||
|
ax |
ay |
|
|
|
|
||
3.2.5. Прямая в отрезках
Возьмем общее уравнение прямой Ах + Ву + С = 0 и преобразуем его:
Ах + Ву = - С; |
Ax |
|
By |
1; C |
a; C |
b ; |
|
C |
C |
||||||
|
|
A |
B |
|
тогда ax by 1 есть уравнение прямой в отрезках; а – отрезок, отсекаемый прямой по оси ОХ; b – по оси ОY.
3.2.6. Взаимное расположение прямых на плоскости
y 
1. Прямая L1 пересекается с прямой L2 (рис.3.6). |
|
M 0 |
|
||||||
а) Угол γ между L1 |
и L2 можно найти по формуле: |
|
|||||||
|
|
|
|
||||||
tg tg 2 1 |
tg 2 |
tg 1 |
или tg |
k2 k1 |
. |
1 |
2 |
|
|
|
|
|
|||||||
1 tg 1 tg 2 |
|
|
|||||||
|
|
|
|||||||
|
0 |
|
x |
||||||
|
|
1 k1k2 |
|
||||||
Угол γ можно найти, используя понятие нормали:
|
|
|
n1 |
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.6 |
||
cos |
|
|
|
|
|
|
|
|
, где n |
A ;B |
– нормаль L1 |
, n |
A ;B – нормаль L2; |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
n1 |
|
|
|
n2 |
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
2 |
2 |
2 |
|
|
|
|||||||
б) точку пересечения М0(х0,у0) найдем, решив систему из уравнений L1 и L2: |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 x B1 y C1 0 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A x B y C |
2 |
0 . |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
||
2. L1 |
|
L2 , следовательно, 1 |
2 и k1 k2 |
или вектор n1 коллинеарен векто- |
|||||||||||||||||||||||||||||
ру n и тогда |
A1 |
|
|
B1 |
|
C1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2 |
|
|
|
|
|
A2 |
|
|
|
|
B2 |
|
C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3. L L |
, следовательно, ctg ctg |
0 |
и |
ctg |
1 k1k2 |
; отсюда условие |
|||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
k2 k1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
перпендикулярности прямых: |
1 k k |
|
0 ; k |
|
|
1 |
или n n 0 . |
||||||||||||||||||||||||||
2 |
2 |
k1 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3.2.7. Расстояние от точки до прямой
Чтобы найти расстояние от т. М0(х0 , у0) до прямой L: Ах + Ву + С = 0, необходимо в общее уравнение прямой, взятое по модулю, подставить координаты точки и поделить на модуль нормали n данной прямой:
d т.M0 ;L |
|
Ax0 |
By0 |
C |
. |
|
|
|
|
|
|
||
|
|
|
|
|||
|
|
|
A2 B2 |
|||
3.2.8. Деление отрезка в данном отношении λ
Пусть задан отрезок АВ, т. А(хА, уА); т. В(хВ, уВ) и т.М(х, у) – делящая точка.
Определение. т. М(х, у) делит отрезок АВ в отношении λ, если AMMB .
26
