МИНИСТЕРСТВО АГРАРНОЙ ПОЛИТИКИ И ПРОДОВОЛЬСТВИЯ УКРАИНЫ

ГОСУДАРСТВЕННОЕ АГЕНТСТВО РЫБНОГО ХОЗЯЙСТВА УКРАИНЫ

КЕРЧЕНСКИЙ ГОСУДАРСТВЕННЫЙ МОРСКОЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра высшей математики и физики

ВЫСШАЯ МАТЕМАТИКА

Часть 1

КОНСПЕКТ ЛЕКЦИЙ

для студентов направлений 6.030504 «Экономика предприятия»,

6.030509 «Учет и аудит»

Керчь 2013 г.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ …………………………………………………………………………. 4 ТЕМАТИЧЕСКИЙ ПЛАН…………………………………………………………. 5

1.ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ………………………………………. 6

1.1.Матрицы. Определители………………………………………………………. 6

1.2.Правило вычисления определителя любого порядка……………………….. 7

1.3.Свойства определителей ……………………………………………………… 8

1.4.Математические операции над матрицами ………………………………….. 8

1.5. Понятие системы линейных алгебраических уравнений …………………… 10 1.6. Решение систем линейных алгебраических уравнений…………………….. 11

2.ВЕКТОРНАЯ АЛГЕБРА………………………………………………………. 15

2.1.Прямоугольная система координат на плоскости и в пространстве………. 15

2.2.Основные понятия……………………………………………………………… 16

2.3.Линейные операции над векторами ………………………………………….. 18

2.4.Разложение вектора по базису…………………………………………………. 19

2.5.Скалярное произведение векторов……………………………………………. 20

2.6.Векторное произведение векторов……………………………………………. 21

2.7.Понятие смешанного произведения векторов……………………………….. 22

3.АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ…………………….. 23

3.1.Линия на плоскости…………………………………………………………… 23

3.2.Прямая линия на плоскости………………………………………………….. 24

3.3.Кривые второго порядка ………………………………………………… 27

3.4.Плоскость в пространстве……………………………………………….. 33

3.5.Прямая линия в пространстве ……………………………………………… 35

4.МАТЕМАТИЧЕСКИЙ АНАЛИЗ ……………………………………………. 37

4.1.Основные понятия………………………………………………………………. 37

4.2.Классификация основных элементарных функций …………………………. 38

4.3.Предел функции ……………………………………………………………….. 40

4.4. Бесконечно малые функции и их свойства…………………………………… 41

4.5.Бесконечно большие функции и их свойства…………………………………. 42

4.6.Основные свойства конечных пределов ……………………………………… 42

4.7.Вычисление пределов………………………………………………………….. 43

4.8.Непрерывность функции в точке …………………………………………….. 45

4.9.Производная функции…………………………………………………………. 47

4.10.Общая схема исследования функции………………………………………... 53

Литература ………………………………………………………………………….. 59

3

ВВЕДЕНИЕ

Последние десятилетия отмечены бурным вторжением математики во все сферы человеческой деятельности. Роль математики как орудия моделирования процессов окружающей нас действительности возросла многократно, и, как следствие этого, резко повысилась роль математического образования.

Математика является фундаментальной дисциплиной. Ее преподавание предусматривает:

развитие логического и алгоритмического мышления;

овладение основными методами исследования и решения математических задач;

выработку умения самостоятельно проводить математический анализ при-

кладных инженерных задач.

Роль математики в экономических исследованиях зачастую не всегда видна явно, в то время как она из вспомогательного средства превратилась в активный метод исследования экономической действительности. На определенных этапах экономических исследований математика становится единственным способом познания. Язык и методы математики оказались весьма продуктивными для развития экономической теории.

Решение многих управленческих и экономических задач строится на рассмотрении зависимостей интересующих нас величин от различных факторов. Функция показывает, как одна величина зависит от другой. Т.е., изучение функциональной зависимости в математике в дальнейшем поможет студентам в решении экономических задач. Для экономики также представляет интерес условие равновесия, т.е. когда спрос равен предложению. Исследование поведения кривых спроса и предложения рассматривается при изучении темы «Приложение производной».

Курс высшей математики для студентов направления «Экономика предприятия», «Учет и аудит» читается два семестра. Содержание курса излагается на лекциях. На практических занятиях студенты овладевают основными методами и приемами решения математических задач.

Данный конспект лекций содержит темы, изучаемые в первом семестре, по каждой из которых приведен теоретический материал, примеры, вопросы для самопроверки. В конце конспекта приведен список учебной литературы. Конспект лекций составлен в соответствии с программой учебной дисциплины и является методическим руководством для систематического изучения общего курса прикладной математики студентами дневной и заочной форм обучения направлений «Экономика предприятия», «Учет и аудит».

4

ТЕМАТИЧЕСКИЙ ПЛАН

Тема 1. Элементы линейной алгебры

Матрицы. Определители. Правило вычисления определителя любого порядка. Свойства определителей. Математические операции над матрицами. Понятие системы линейных алгебраических уравнений. Решение систем линейных алгебраических уравнений. Правило Крамера решения СЛАУ. Матричный способ решения. Метод Гаусса (метод последовательного исключения неизвестных).

Тема 2. Векторная алгебра

Декартова прямоугольная система координат на плоскости и в пространстве. Основные понятия. Линейные операции над векторами. Разложение вектора по базису. Скалярное произведение векторов. Векторное произведение векторов. Понятие смешанного произведения векторов.

Тема 3. Аналитическая геометрия на плоскости

Линия на плоскости. Прямая линия на плоскости. Общее уравнение прямой. Прямая с угловым коэффициентом. Пучок прямых. Прямая, проходящая через две заданные точки. Прямая в отрезках. Взаимное расположение прямых на плоскости. Расстояние от точки до прямой. Деление отрезка в данном отношении. Кривые второго порядка. Окружность. Эллипс. Гипербола. Парабола. Общее уравнение кривой второго порядка. Плоскость в пространстве. Общее уравнение плоскости. Неполные уравнения плоскости. Уравнение плоскости в отрезках. Уравнение плоскости, проходящей через три заданные точки. Взаимное расположение двух плоскостей в пространстве. Расстояние от точки до плоскости. Геометрический смысл СЛАУ. Прямая линия в пространстве. Общие уравнения прямой. Канонические уравнения прямой. Параметрические уравнения прямой. Прямая, проходящая через две заданные точки. Приведение общих уравнений прямой к каноническому виду. Взаимное расположение прямой и плоскости. Взаимное расположение двух прямых в пространстве.

Тема 4. Математический анализ

Основные понятия. Классификация основных элементарных функций. Предел функции. Бесконечно малые функции и их свойства. Бесконечно большие функции и их свойства. Основные свойства конечных пределов. Вычисление пределов. Непрерывность функции в точке. Основные понятия. Классификация точек разрыва. Свойства функций, непрерывных в точке. Свойства функции, непрерывной на отрезке. Производная функции. Основные понятия. Свойства производной. Таблица основных производных. Дифференциал функции. Геометрический смысл дифференциала. Производные высших порядков. Правило Лопиталя. Общая схема исследования функции. Область определения функции. Интервалы монотонности функции. Точки экстремума. Интервалы выпуклости-вогнутости графика функции. Точки перегиба. Асимптоты. Четность, нечетность и периодичность функции. Нули функции и дополнительные точки. График функции.

5

1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ 1.1. Матрицы. Определители

Определение. Матрицей называется прямоугольная таблица из чисел или иных математических объектов, расположенных в m строках и n столбцах. Обозначают матрицы А, В, С, … Общий вид матрицы

где aij – элемент матрицы А, i – номер строки, j – номер столбца, в которых расположен aij. Выражение m n называется размерностью матрицы.

Если m ≠ n – матрица А прямоугольная;

m = n – матрица А квадратная и число n – её порядок; m = 1 – матрица А есть матрица-строка;

n = 1 – матрица А есть матрица-столбец.

Квадратная матрица имеет главную и побочную диагонали. Главную диагональ составляют элементы с одинаковыми индексами: а11, а22, …, аnn.

Квадратная матрица, все элементы которой над главной или под главной диагональю – нули, называется матрицей треугольного вида.

Диагональная матрица – квадратная матрица, все элементы которой – нули, кроме элементов главной диагонали.

Единичная матрица – диагональная матрица, на главной диагонали которой стоят единицы. Обозначается чаще всего Е.

Ноль-матрица – матрица любой размерности, все элементы которой нули. Все квадратные матрицы имеют специальную характеристику – определи-

тель.

Определение. Определителем матрицы А называется число или математическое выражение, получаемое из элементов данной матрицы А по определенному правилу.

Обозначение : , A, det A, A .

Пусть А – квадратная матрица n-го порядка.

Определение. Минором Mij элемента aij матрицы А называется определитель (n – 1)-го порядка, полученный из A вычеркиванием i-ой строки и j-го столбца.

6

1 2

2)A . Указать алгебраическое дополнение элемента а21.

3 4

а21=3; М21 = 2; A21 1 2 1 2 2 .

Будем называть рядом определителя (матрицы) строку или столбец определителя (матрицы).

1.2. Правило вычисления определителя любого порядка

Теорема Лапласа. Определитель матрицы А n-го порядка равен сумме парных произведений элементов любого ряда на свои алгебраические дополнения.

Рассмотрим частные случаи.

1) Определитель 2-го порядка.

ведению элементов по главной диагонали минус произведение элементов по побочной диагонали.

2) Определитель 3-го порядка.

В данном случае можно вычислить определитель, раскрывая его по любой строке или любому столбцу (6 возможностей).

a11 a22a33 a32a23 a12 a21a33 a31a23 a13 a21a32 a31a22 .

7

9 36 27 0

При вычислении определителей 3-го порядка используют правило треугольников.

1.3. Свойства определителей

Определение . Операция, при которой каждая строка определителя (матрицы) становится соответствующим по номеру столбцом, называется транспонированием.

1)Транспонирование не изменяет величины определителя.

2)Если все элементы какого-либо ряда определителя – нули, то определитель равен нулю.

3)Если все элементы какого-либо ряда определителя имеют общий множитель, то его можно вынести за определитель.

Следствие. Чтобы умножить определитель на число, достаточно умножить на это число все элементы какого-либо ряда.

4)Если определитель содержит два одинаковых или два пропорциональных ряда, то определитель равен нулю.

5)Если в определителе поменять местами два соседних ряда, то определитель изменит знак на противоположный.

6)Если к элементам какого-либо ряда прибавить элементы другого ряда, умноженные на число , то определитель не изменится.

Говорим, что линейные операции над строками (столбцами) определителя не изменяют его величину.

7) Определитель треугольного вида и определитель диагонального вида равен произведению элементов, стоящих на главной диагонали:

1.4. Математические операции над матрицами

1.А = В, если А и В имеют одинаковые размерности и равны их соответствующие элементы aij bij .

2.A B , при сложении (вычитании) матриц одинаковой размерности складываются (вычитаются) соответствующие элементы.

3.A, при умножении матрицы А на число α каждый элемент матрицы умножается на это число.

8

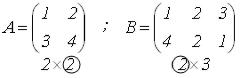
Следствие. Если все элементы матрицы имеют общий множитель, то его можно вынести за знак матрицы, как сомножитель.

Операции 1, 2, 3 называются линейными операциями над матрицами.

Свойства линейных операций.

1)А + В = В + А (коммутативность);

2)(А + В) + С = А + (В + С) (ассоциативность);

3)α (А + В) = αА + αВ (дистрибутивность);

4)А + 0 = А.

4. A B , перемножаются только согласованные матрицы.

Определение. Матрицы А, B называются согласованными на произведение A B , если число столбцов первого сомножителя А равно числу строк второго сомножителя В.

Правило перемножения матриц A B C :

Каждый элемент сij матрицы С равен сумме парных произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В, т.е. перемножение производится по правилу «строка на столбец». Матрица С будет иметь столько строк, сколько имеет матрица А, и столько столбцов, сколько имеет матрица В.

Пример.

размерность 2 3.

Операция перемножения матриц в общем случае некоммутативна A B B A . Умножение матрицы на единичную матрицу коммутативно.

5. Обращение матрицы.

Определение. Квадратная матрица, определитель которой равен нулю, называется вырожденной. В противном случае матрица невырожденная.

Всякая невырожденная матрица А имеет обратную матрицу А-1. Определение. Матрица А-1 называется обратной к матрице А, если их про-

изведение дает единичную матрицу E, т.е. A A 1 A 1 A E .

Правило обращения матрицы А, n = 3.

матрицы А.

9