10 Нерозгалужене коло з активним опором та ємністю

Усякий конденсатор має втрати, тобто активну потужність. Тому реальний конденсатор можна представити схемою послідовного з’єднання активного і реактивного ємнісного елементами. Активний опір визначається потужністю втрат:

Розглянемо коло змінного струму з послідовно з’єднаними резистивним та ємнісним елементами (рис.10.1), по яким проходе синусоїдний струм:

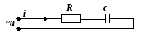
Рисунок 10.1 - Послідовне сполучення резистивного та ємнісного опорів

Діючий струм однаковий на усіх елементах, так як вони з’єднанні послідовно.

Вияснимо, якою буде напруга прикладена до кола, яка розходується у двох опорах:

1. спад напруги на активному опорі збігається за фазою зі струмом і його миттєве значення буде:

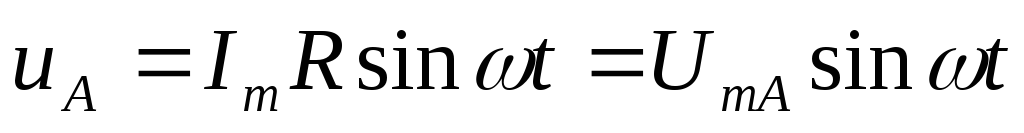
діюче:

2. спад напруги на ємнісному опорі відстає за фазою струм на кут 90º і його миттєве значення: діюче: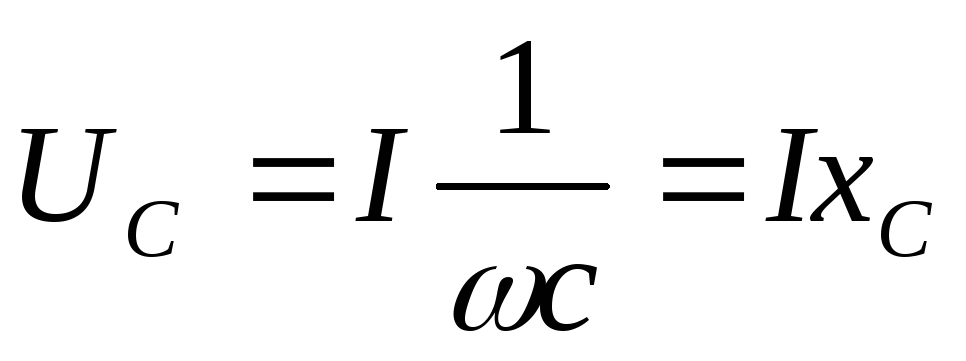

За ІІ законом Кірхгофа миттєве значення повної напруги (на затискачах кола) у будь-який час дорівнює геометричній сумі падінь напруги на окремих елементах::

Потрібно розуміти, що у конденсатора не має двох таких точок, між якими була б прикладена напруга , і у резистивного елемента не має двох таких точок, між якими була б прикладена напруга. Фізичною величиною є сума цих напруг, тобто напруга на кінцях конденсатора є напругою джерела. Розділення напруги на затискачах кола на складові є лише зручним прийомом для розрахунків.

Активна напруга переборює активний опір, а реактивна врівноважує ЕРС конденсатора. Так як усі падіння напруги синусоїдні величини однакової частоти, то і їх сума є синусоїдною величиною той же частоти.

Побудуємо векторну діаграму струму та напруг і трикутники напруг та опорів (рис.10.2).

Для побудови векторної діаграми використовуємо діючі значення струму і напруг. За вихідний вектор приймають вектор струму, який збігається з позитивним напрямком вісі абсцис при початковій фазі нуль. Вектор активної напруги відкладають за напрямком вектора струму, а вектор ємнісної напруги проводять під кутом -90º до вектора струму (за годинниковою стрілкою). За правилом паралелограма отримуємо вектор діючого значення повної напруги . Таким чином, вектори,іутворюють прямокутний трикутник, який називають трикутником напруг. З векторної діаграми видно, що напруга на затискачах розглядаємого кола відстає за фазою від струму на кут:

де φ - зсув фаз між прикладеною напругою та струмом:

Трикутник опорів можна отримати, якщо всі сторони трикутника напруг зменшити у I раз (рис10.2). Опори кола постійні величини, тому їх не можна зображати векторами. Якщо помножити сторони трикутника напруг на діюче значення струму у колі I, то отримаємо подібний трикутник потужностей (рис.10.2).

Потрібно звернути увагу: вектори індуктивних складових напруги, опору, потужності мають зсув відносно вектора активної напруги на кут 90º за напрямком обертання векторів, а вектори ємнісної складової напруги, опору, потужності - на кут 90º проти напрямку обертання векторів.

З трикутників напруг та опорів видно, що діюче значення прикладеної напруги і повний опір кола будуть:

Аналогічно визначаються амплітудні значення напруг:

Тоді, закон Ома для діючих і амплітудних значень цього кола буде:

та

Для миттєвих значень закон Ома використовуватися не можна , так як

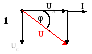
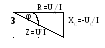
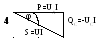
Рисунок 10.2 - Векторна діаграма (1), трикутники напруг (2), опорів (3) та потужностей (4) у колі з послідовним сполученням резистивного та ємнісного елементів

Зсув фаз з трикутників напруг, опорів та потужностей визначити можна як:

Побудуємо хвильові діаграми струму, напруг і потужності (рис.10.3).

Наруга відстає від струму на кут . Миттєва потужність дорівнює нулю, коли напруга або струм будуть дорівнювати нулю, так як. Якщо струм і напруга мають однакові знаки, то миттєва потужність позитивна, і коло споживає енергію від джерела. У ті частини періоду, коли напруга і струм мають різні знаки, миттєва потужність негативна, і деяка частина енергії повертається до генератора.

Миттєва потужність, яку розвиває джерело енергії у колі, це добуток миттєвих значень струму та напруги:

Таким чином, миттєва потужність складається з постійної складової () і синусоїдної складової, яка змінюється з подвійною частотою при зрівнянні з частотою струму і має амплітуду. Зміна складова потужності змінюється за гармонічним законом, то її середня потужність за період дорівнює нулю.

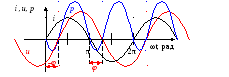
Рисунок 10.3 - Хвильові діаграми струму, напруг і потужності у колі з послідовним сполученням резистивного та ємнісного елементів

Тому середня потужність за період чи активна потужність кола дорівнює постійній складовій миттєвої потужності:

При заданих незмінно діючих значеннях напруги і струму активна потужність змінюється в залежності від від нуля придо максимально можливої потужності у коліпри(коли коло має лише активне навантаження). Тоді, середня потужність в активному опорі - це активна потужність усього розглядаємого кола, тобто активна потужність кола розходується лише на резистивному елементі.

Реактивна потужність кола є виміром величини обміну енергії між джерелом і електричним полем діелектрика конденсатора:

Повна потужність кола:

Таким чином, енергетичний процес у цьому колі складається з двох процесів:

по-перше - частка енергії безповоротно передається від джерела до активного

опору, де перетворюється у інші форми енергії,

по-друге - частка енергії коливається між джерелом і електричним полем

приймача.

Чим менше коефіцієнт потужності, тим більшу роль грають ці безкорисні коливання енергії.

З (рис.10.3) зрозуміло, що площі розміщенні вище вісі абсцис пропорційні позитивній енергії, яка безповоротно передається від джерела до кола, а площі розміщенні нижче вісі абсцис пропорційні негативній енергії, яка за певні проміжки часу повертається з електричного поля діелектрика конденсатора до джерела. Різниця цих площин уявляю собою площу пропорційну енергії, яка за один період розходується в активному опорі на безповоротні процеси. Позитивна енергія більша за негативну енергію.

Якщо коло має кілька послідовно з’єднаних резистивних та ємнісних елементів, то закон Ома буде мати вигляд:

де () - сума усіх активних (ємнісних) опорів,Ом