Зміст

Лекція 1 Вступ. Поняття про теорію ймовірностей. Зміст і завдання предмету. Основні поняття теорії ймовірностей. Класичне, статистичне та геометричне означення ймовірності

Лекція 2 Операції над подіями. Теорема додавання ймовірностей. Умовні ймовірності . Теорема множення ймовірностей. Ймовірність здійснення принаймні однієї з незалежних подій

Лекція 3 Формула повної ймовірності. Формули Байєса

Лекція 4 Схема незалежних випробувань. Формула Бернуллі. Локальна та інтегральна теореми Муавра - Лапласа. Формула Пуассона

Ле­к­ція 5 Озна­чен­ня ви­па­д­ко­вої ве­ли­чи­ни. Фу­н­к­ція розпо­ді­лу ви­па­д­ко­вої ве­личи­ни та її вла­с­ти­во­с­ті. Дискретні випадкові величини та їх розподіли

Лекція 6 Неперервні випадкові величини та їх розподіли

Лекція 7 Числові характеристики випадкової величини

Лекція 8 Закон великих чисел. Центральна гранична теорема

Лекція 9 Завдання математичної статистики. Генеральна сукупність і вибі­рка. Варіаційний ряд. Графічне зображення вибірки

Лекція 10 Числові характеристики вибірки. Статистична функція розподілу

Лекція 11 Точкові та інтервальні оцінки параметрів розподілу. Довірчі інтервали для параметрів нормального розподілу

Лекція 12 Поняття статистичної гіпотези. Статистичний критерій. Критерій Пірсона. Критерій Колмогорова

Лекція 13 Поняття про кореляційну залежність. Лінійна кореляція. Метод найменших квадратів

Лекція 14 Поняття про дисперсійний аналіз. Однофакторний дисперсійний аналіз

Список літератури

Додаток А Таблиці значень функцій

4

8

11

14

17

21

25

29

31

34

36

39

42

44

47

48

Лекція 1 Вступ. Поняття про теорію ймовірностей. Зміст і завдання предмету. Основні поняття теорії ймовірностей. Класичне, статистичне та геометричне означення ймовірності

Події в навколишньому світі можна поділити на вірогідні, неможливі та випадкові. Перші при реалізації певного комплексу умов (при випробуванні) відбуваються завжди, другі –ніколи, треті – можуть як відбуватися, так і не відбуватися. Віднесення певної події до тієї або іншої групи істотно залежить від умов випробування. Наприклад, розглянемо подію, зв’язану з попаданням у мішень. Для цього треба, щоб хтось стріляв, щоб була мішень, щоб був засіб реалізації попадання , щоб цей засіб був доступний (справжній), щоб була забезпечена певна відстань до мішені і т.д. Якщо якась з умов не виконана, то подія буде неможливою; якщо будуть виконані всі необхідні і достатні умови, то подія буде достовірною (скажімо пістолет упирається в мішень).

Основним тут є поняття випробування. Під випробуванням розуміємо забезпечення всіх необхідних умов для появи даної події. Події позначають літерами латинської абетки А, В, С, ....

Випадкові події займають проміжну позицію між “ завжди” і “ ніколи”. І можуть наставати чи не наставати в даному випробуванні, в якому виконані всі необхідні умови появи їх. Стосовно достатніх умов зазначимо, що вони не завжди підконтрольні, а про деякі з них важко здогадатися. Так, ми не контролюємо пориву вітру чи спалаху блискавки, які могли спричинити наш промах по мішені. У такій ситуації не можна обмежитися одиничними випробуваннями, а треба мати якомога більшу їх кількість і аналізувати всю множину отриманих результатів. Ця множина є більш стійкою, оскільки одна частина попадань відхиляється в один бік, а друга в другий, і ці випадкові відхилення взаємно компенсуються, відкриваючи шлях до закономірності.

Ось чому теорія ймовірності як наука про числову міру випадковості подій передбачає вивчення не одиничних, а масових однорідних випадкових подій, які підпорядковуються стохастичним ( від грець. “стохастіс” – здогадка ) закономірностям, встановлення яких і є її основною задачею.

Виникнення теорії ймовірностей , обумовлене спробою побудувати теорію азартних ігор, відноситься до ХVІ-ХVІІ ст.. і зв’язане з іменами таких учених, як Дж. Кардано, Б. Паскаль, Х. Гюйгенс, П. Ферма. Найістотнішим досягненням її першого періоду є відкриття Д. Бернуллі закону великих чисел. Другий період розвитку теорії ймовірностей зв’язаний з іменами Лапласа, Пуассона, К. Гаусса, Буняковського ( ХVІІ-ХІХ ст.). Як наука теорія ймовірностей сформувалась на межі ХІХ – ХХ ст.. завдяки зусиллям П.Л.Чебишева, О.М.Ляпунова, О.О.Маркова, Р. Мізеса. Проте в 30-х роках нашого століття вона стала повноцінним розділом математики ( до цього вважалась прикладною дисципліною) завдяки чіткому поняттю ймовірності, даному .М.Колмогоровим.

Подамо кілька означень.

Випадкові події поділяються на сумісні й несумісні . У першому випадку поява однієї події не виключає, а в другому виключає появу другої події. Наприклад, осічка і непопадання в ціль – сумісні, осічка і попадання в ціль – несумісні події.

Кілька подій утворюють повну групу, якщо поява хоч однієї з них – вірогідна подія. Наприклад, поява аверса і реверса при киданні монети, поява числа очок від одиниці до шести при киданні гральної кості, попадання і промах.

Кілька подій називають рівноможливими, якщо при випробуванні вони з’являються однаково часто. Так, аверс і реверс- рівноможливі, але попадання і промах, як правило, - ні.

Деякі події наступають досить часто, а деякі – навпаки, дуже рідко. Введемо числову характеристику показника настання події.

Означення Ймовірністю Р даної події А називається відношення числа результатів випробувань m, які сприяють появі даної події, до загального числа n рівноможливих і єдино можливих результатів випробувань, які утворюють повну групу, тобто

Р (А) = m / n (1.1)

Наведене означення називається класичним.

З означення випливають властивості ймовірності: для вірогідних подій Р = 1

( m = n ), для неможливих Р = 0 ( m = 0), для випадкових 0 < P < 1 (0 < m < n).

Приклад

У групі з 25 студентів п’ять дівчат. Знайти ймовірність того, що з цієї групи першою до аудиторії зайде дівчина.

Розв’язування. Маємо Р (А) = 5 / 25 = 0,2

Приклад

Знайти ймовірність того , що при киданні гральної кості випаде грань з парною кількістю очок .

Розв’язування. Маємо n = 6, m = 3. Отже, Р (А) = 0,5.

Класичне означення ймовірності, з одного боку, просте, наочне, конструктивне, а з другого боку, воно має ряд суттєвих недоліків, а саме: не завжди можна подати результат випробувань як сукупність рівно можливих результатів; m і n скінченні, але це не завжди так; рівноможливість і рівноймовірність –синоніми. Отже , формула (1.1) не є коректним означенням. Геометричне означення ймовірності з’явилося завдяки спробі відмовитися від скінченності величин m і n. Воно полягає в тому, що

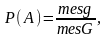
де mes g і mes G - міри ( довжини, площі, об’єми) простору всіх (G) результатів і сприятливих (g) результатів.

Приклад

Два студенти домовилися зустрітися в певному місці між 15-ю та

16-ю год. Перший, хто прийде, чекає на другого не більше 20 хв. Яка ймовірність їхньої зустрічі?

Розв’язування. Нехай х – час приходу першого, а у – другого студента. Тоді mes G = 1 - площа квадрата зі стороною, яка дорівнює одиниці (рис. 1). Умова зустрічі має вигляд у - х , тобто 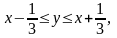звідки маємо

mes g = 5/9. Отже, Р (А) = 5 / 9.

у 16

q

15 16 x

Рисунок 1

Наведемо статистичне означення ймовірності: основним поняттям тут є відносна частота появи подій в результаті проведених випробувань

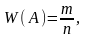
де n – число проведених випробувань, а m – число випробувань, в яких відбувалася подія А.

Ймовірність – це теоретична величина, обчислена до чи без проведення випробувань, відносна частота – величина емпірична, обчислена за результатами випробувань.

Визначення величини W (А) для різних подій показало, що в одних випадках вона для різних серій випробувань змінюється мало, а в других – істотно.

Якщо W (A) ≈ C, то подію А називають статистично стійкою, в решті випадків – нестійкою. У подальшому останні ситуації не розглядатимемо (це, як правило, ситуації, обумовлені “людським фактором”).

Переважна більшість помилок, зв’язаних із застосуванням теорії ймовірностей, пояснюється її спробами аналізувати невизначені події, які дістаємо у випробуваннях з великим числом неконтрольованих умов (про яку ймовірність виграшу команди можна вести мову, якщо тренери заздалегідь домовилися про нічию). Через це в означенні випадкової події обов’язково слід передбачити її статистичну стійкість.

Означення Статистичною ймовірністю події А називається число, навколо якого групуються відносні частоти цієї події або сама частота.

Р.Мізес встановив, що для випадкових подій

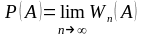
(для невизначених подій така границя не існує).

У 1900 р. відбувся Другий всесвітній математичний конгрес, на якому Д.Гільберт висунув 23 найважливіші проблеми. Шоста проблема Гільберта – побудова логічних несуперечливих основ теорії ймовірностей. Цю проблему було розв’язано через 33 роки О.Колмогоровим, який запропонував таку систему аксіом, яка дає означення ймовірностей:

1. кожній випадковій події А відповідає невід’ємне число Р (А), яке називається ймовірністю цієї події,

2. для вірогідної події U Р (U)=1,

3. ймовірність появи хоча б однієї з попарно несумісних подій дорівнює

сумі ймовірностей цих подій.

Домашнє завдання

1. Скільки різних двозначних чисел можна утворити із цифр 2, 3, 4, 5, 6, 7?

2. У групі із 25 осіб потрібно обрати 5 осіб на 5 різних посад. Скількома способами це можна зробити?

3. Скільки різних перестановок можна утворити із букв слова "фізика"?

4. На карточках написані букви "а", "в", "м", "к" , "о", "с". Карточки розкладають в ряд. Яка ймовірність отримати слово "Москва"?

5. У групі із 25 учнів розігрують 4 різні путівки. Яка ймовірність того, що всі путівки отримають деякі з 20 учнів, що подали заяви раніше?

6. У групі 20 юнаків і 10 дівчат. На зліт студентів обирають 8 учасників. Яка ймовірність обрати 5 юнаків і 3 дівчат?

7. Підкидають 2 гральні кубика. Знайти ймовірність того, що сума чисел буде більша, ніж добуток.

8. Із куль, занумерованих усіма двозначними числами, вибирається одна. Яка ймовірність того, що її номер не містить 0?

9. Навмання взято два додатних числа, кожне з яких не перевищує 1. Знайти ймовірність того, що їх сума не перевищує 1, а добуток не перевищує 2/9.

10. В середину круга радіуса 10 навмання кидають точку. Знайти ймовірність того, що точка попаде в середину вписаного в круг правильного трикутника.

Лекція 2 Операції над подіями. Теорема додавання ймовірностей. Умовні ймовірності. Теорема множення ймовірностей. Ймовірність здійснення принаймні однієї з незалежних подій

Означення Протилежними називаються події А і 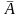( не А), які утворюють повну групу (рис. 2).

А

Рис. 1

Рисунок 2

Прикладом А і є поява аверса і реверса при киданні монети.

Означення Добутком подій А і В називається подія А·В, яка полягає в одночасній появі А і В (рис.3).

А·В

В

А

Рисунок 3

Означення Сумою подій А і В називається подія А + В , яка полягає в появі А або В ( або АВ ) (рис.4).

А В

А + В

Рисунок 4

Аналогічно визначаються добуток і сума більшого числа подій.

Теорема 1 Імовірність суми сумісних подій А і В дорівнює сумі ймовірностей цих подій без ймовірності їх добутку

Р ( А + В) = Р (А) + Р (В ) - Р ( А·В)

Теорема 2 Якщо А і В несумісні, то А·В =V, Р (А·В) = 0 і тоді ймовірність суми несумісних подій А і В дорівнює сумі ймовірностей цих подій

Р ( А + В ) = Р (А ) + Р ( В ).

Останнє співвідношення можна використати як означення несумісних подій.

Н а с л і д о к 1. Якщо події А_1, А_2, . . . А_n попарно несумісні, то

Р (А₁ + А₂ + . . .+ А_n ) = Р (А₁) + Р ( А₂) + . . . + Р ( А_n)

(треття аксіома А. Колмогорова).

Н а с л і д о к 2. Сума ймовірностей попарно несумісних подій, які утворюють повну групу, дорівнює одиниці:

Р ( А₁ ) + Р ( А₂ ) + . . . +Р (А_n) = 1

Н а с л і д о к. 3. Сума ймовірностей взаємо протилежних подій дорівнює одиниці:

Р ( А ) + Р ( ) = 1.

Так, якщо ймовірність влучення в ціль Р (А) = 0,8, то ймовірність промаху q = 1 – Р ( А) = 0,2.

Події А і В можуть бути залежними й незалежними. У першому випадку поява А впливає, а в другому не впливає на ймовірність появи В.

Приклад

У ящику чотири білих і три чорних кулі. В результаті першого випробування ( вилучення кулі з ящика) з’явилася чорна куля ( подія А). Знайти ймовірність появи білої кулі ( подія В) в другому випробуванні, якщо: а) кулю повертають в ящик, в) кулю не повертають після першого випробування.

Розв’язування. Маємо а) Р(В) = 4 / 7 – незалежна подія;

в) Р ( В/А ) = 4 / 6 = 2 / 3 – залежна подія.

Означення Умовною ймовірністю Р (В/А ) називається ймовірність події В за умови, що подія А відбулась.

Теорема 3 Ймовірність добутку двох залежних подій А і В дорівнює добутку ймовірності однієї з цих подій на умовну ймовірність іншої

Р ( А·В ) = Р (А)· Р (В/А) = Р (В)· Р ( А /В ).

Н а с л і д о к. Р (В / А ) = Р ( А·В) / Р ( А ).

Теорема 4 Ймовірність добутку незалежних подій А і В дорівнює добутку ймовірностей цих подій

Р ( А·В ) = Р (А )· Р ( В ).

Ця теорема випливає з попередньої. Крім того, можна довести, що коли А і В незалежні, то незалежні також А 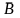і , і В, і .