Ймовірність появи хоча б однієї події

Нехай події А₁, А₂, ... ,А_n незалежні в сукупності, причому Р(А₁)= р₁,

Р(А₂)= р₂,..., Р(А_n)= р_n ; нехай внаслідок випробування можуть наступити всі події, або частина з них, або жодна з них.

Ймовірність настання події А, що полягає в появі хоч би однієї з подій А₁, А₂, ... ,А_n , незалежних в сукупності, рівна різниці між одиницею і добутком ймовірностей протилежних подій ..., :

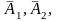Р(А) =1 - q₁q₂…q_n, де q₁ = 1-р₁; q₂ = 1-р₂; q_n = 1- р_n.

Зокрема, якщо всі n подій мають однакову ймовірність, рівну р, тоді ймовірність появи хоч би однієї з цих подій

Р(А) =1 – qⁿ , де q = 1 ─ р.

Приклад

У електричний ланцюг послідовно ввімкнені 3 елементи, що працюють незалежно один від іншого. Ймовірність відмови першого, другого і третього елементів відповідно рівні р₁ = 0,1; р₂ = 0,15; р₃ = 0,2. Знайти ймовірність того, що струму в ланцюгу не буде.

Розв’язування. Оскільки елементи ввімкнені послідовно, то струму в ланцюгу не буде (подія А), якщо відмовить хоча б один з елементів.

Шукана ймовірність

Р(А) = 1─ q₁q₂q₃ = 1─ ( 1─ 0,1)(1─ 0,15)(1 ─ 0,2) = 0,388.

Приклад

Ймовірність хоч би одного попадання стрільцем в мішень при трьох пострілах дорівнює 0,875 . Знайти ймовірність попадання при одному пострілі.

Розв’язування. Ймовірність попадання в мішень хоч би при одному з трьох пострілів (подія А) дорівнює Р(А) = 1-q³ , де q – ймовірність промаху.

По умові Р(А) = 0,875. Отже, 0,875= 1-q³ , або q³ =1 - 0,875 = 0,125.

Звідси

Шукана ймовірність p = 1 – q = 1 – 0,5 = 0,5.

Домашнє завдання

1. Підкидають гральний кубик. Знайти ймовірність того, що випаде непарне число або число кратне 3.

2. Студент знає 25 із 30 питань програми. Знайти ймовірність того, що студент знає запропоновані йому три питання в білеті.

3. Прилад складається з двох елементів, що працюють незалежно. Ймовірність виходу з ладу першого елементу - 0,05, другого - 0,08. Знайти ймовірність того, що при вмиканні приладу

а) вийдуть з ладу обидва елемента;

б) вийде з ладу хоча б один елемент;

в) вийде з ладу тільки один елемент;

г) будуть працювати обидва елемента.

4. З ящику, що містить 25 червоних і 15 синіх кульок, навмання вибирають 3кульки. Знайти ймовірність того, що серед вибраних кульок не більше однієї синьої.

5. Три стрілки провели залпи по мішеням. Ймовірність влучення у ціль у першого стрілка дорівнює 0,8, у другого і третього відповідно 0,7 та 0,9. Знайти ймовірність того, що:

а) тільки один із них влучить у ціль;

б) хоча б один влучить у ціль.

Лекція 3 Формула повної ймовірності. Формули Байєса

Нехай задані випадкові події Н₁, Н₂, . . . Н_n такі, що виконуються дві умови

1) Н₁ + Н ₂ + . . . . + Н_n = U ;

2) Н_j ·Н_k = V j ≠ k

Перша з цих умов означає, що за умов даного комплексу хоч одна з подій Н_k,

k = 1….n, відбудеться. Друга умова означає, що події Н_k попарно несумісні між собою. За виконання умов 1), 2 ) множина подій Н₁, Н ₂ . . . . Н_n називається повною групою подій.

Теорема Якщо Н₁, Н ₂ . . . . Н_n - повна група подій, Р (Н_k)> 0 для k= 1, 2,…..n, то для будь-якої випадкової події А виконується рівність

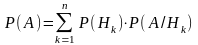
На рис.5 зображена ситуація про яку йдеться в теоремі ( на рисунку n = 4).

H₁ H₂

_А

H₃ H₄

Рисунок 5

Події АН₁, ..... АН_n несумісні і в сумі дають подію А, тому використовуючи теореми про ймовірність суми та добутку подій, маємо

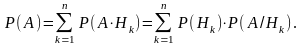
Теорему доведено.

Приклад

Одну і ту ж деталь виготовляють на трьох верстатах. Ймовірність браку на першому верстаті дорівнює 0,010, на другому – 0,015, на третьому – 0,020. Продуктивність першого верстата у 1,5 рази більша за продуктивність другого, продуктивність третього верстата у 2,5 рази більша за продуктивність другого. Усі деталі складаються до одного ящика. Чому дорівнює ймовірність того, що взята навмання деталь з ящику буде бракованою?

Розв’язування. Розглянемо такі випадкові події:

А – деталь бракована;

Н₁- деталь виготовлена на першому верстаті;

Н₂ - деталь виготовлена на другому верстаті;

Н₃ - деталь виготовлена на третьому верстаті.

Спочатку обчислимо ймовірності Р (Н_k). Покладемо Р (Н₂) = p. Тоді за умовою маємо, що Р (Н₁) = 1,5p; Р (Н ₃)= 2,5p. Звідси випливає ( враховуючи, що

Р(Н₁) + Р(Н₂) +Р(Н₃) =1 ) 1,5p + p + 2,5p = 1, тобто 5p =1, p = 0,2. Тому

Р (Н₂ ) = p =0,2; P (H₁) = 1,5p = 1,5 • 0,2 = 0,3; P (H₃) = 2,5 p =2,5 • 0,2 = 0,5.

За умовою задачі Р (А/Н₁ ) = 0,010; Р (А/Н₂ ) = 0,015; Р (А/Н₃) = 0,020.

Тому маємо Р (А ) = Р(Н₁) Р (А/Н₁ ) + P (H₂) Р (А/Н₂ ) + +P (H₃) Р (А/Н₃) = 0,3• 0,010 + 0,2• 0,015 +0,5• 0,020 = 0,016.

Іноді у ситуації, про яку сказано в теоремі, відомо, що подія А вже відбулася, і запитується, яка ймовірність того, що при цьому відбулася випадкова подія Н_k . Відповідь на це питання дає

Теорема ( формули Байєса). Якщо Н₁, Н ₂ . . . . Н_n - повна група подій,

то

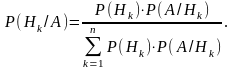
Ця формула зветься ще формулою ймовірності гіпотез – вона дає можливість обчислити ймовірність гіпотези Н_k за умови, що ми знаємо наслідок А.

Для доведення формули зауважимо, що

Р(А Н_k) = Р(А) Р(Н_k /А) = Р(Н_k) ) Р (А /Н_k )

Звідси маємо

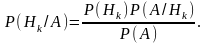
Для остаточного доведення формули досить підставити в останню формулу Р (А) її значення за формулою повної ймовірності.

Приклад

Знову розглянемо ситуацію, яка викладена у задачі про три верстати. Відомо, що витягнута деталь – бракована. Яка ймовірність того, що вона виготовлена на третьому верстаті?

Розв’язування. Усі необхідні ймовірності ми вже знаємо (див. попередній приклад). Тому маємо за формулою Байєса

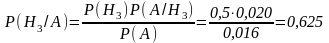
Бачимо, що переважна кількість бракованих деталей виготовлена на третьому верстаті.