
- •Домашнє завдання
- •Ймовірність появи хоча б однієї події
- •Домашнє завдання
- •Домашнє завдання
- •Домашнє завдання
- •Величини та її властивості. Дискретні випадкові величини та їх розподіли
- •5. Розподіл Пуассона ( закон розподілу рідкісних подій)
- •Домашнє завдання
- •Домашнє завдання
- •Властивості математичного сподівання
- •Домашнє завдання
- •Домашнє завдання
- •Числові характеристики вибірки
- •Домашнє завдання
- •Домашнє завдання
- •Лекція 12 Поняття статистичної гіпотези. Статистичний критерій.
- •Критерій згоди Колмогорова
- •Домашнє завдання
- •Домашнє завдання
- •Домашнє завдання
Домашнє завдання
У збиральника є 85 деталей, 31 з яких виготовлено у першому цеху, 29-удругому і 25 - у третьому. Ймовірність того, що деталь виготовлена у першому цеху стандартна, дорівнює 0,9, для другого цеху - 0,8 і для третього - 0,85. Яка ймовірність того, що навмання взята збиральником деталь не стандартна?
Є дві урни: в першій 30 білих і 20 чорних кульок, в другій 40 білих і 35 чорних. З першої урни в другу перекладають не дивлячись одну кульку. Після цього з другої урни беруть одну кульку. Знайти ймовірність того, що кулька чорна.
Деталі для збірки вузлу виготовляються на двох станках, з яких перший виробляє 80% деталей, а другий - 20%. Перший станок виробляє в середньому 4% бракованих деталей, а другий - 3%. Знайти ймовірність того, що навмання взята деталь доброякісна.
При розриві снаряду виникає 6% крупних осколків, 57% - середніх і 37% -дрібних. Ймовірність пробивання броні крупним осколком дорівнює 0,7, середнім — 0,2, дрібним 0,001 Відомо, що у броню потрапив один осколок. Визначіть ймовірність того, що броня пробита.
На двох автоматах виготовляються однакові деталі, які надходять на загальний конвейєр. Продуктивність першого автомату втричі більше продуктивності другого. Перший автомат в середньому виготовляє 95% деталей першого гатунку, а другий 97%. Взята навмання деталь опинилась першогу гатунку. Знайти ймовірність того, що ця деталь виготовлена другим автоматом.
Є три партії деталей по 50 штук у кожній. Кількість стандартних деталей упершій, другій і третій партіях відповідно дорівнює 49, 48, 40. З довільно вибраної партії навмання витягнута деталь, яка опинилася стандартною. Знайти ймовірність того, що деталь була витягнута з третьої партії.
Лекція 4 Схема незалежних випробувань. Формула Бернуллі.
Локальна та інтегральна теореми Муавра - Лапласа. Формула Пуассона
На практиці досить часто використовують схему однакових незалежних випробувань, в кожному з яких повна подія А настає з однією і тією ймовірністю. При цьому знаходять ймовірність того , що в n випробуваннях подія А настає k разів ( 0 ≤ k ≤ n ) . Розглянемо подію В1 , в якій перші k разів подія А настала, а потім в n – k випробуваннях не настала, тобто
В1
=
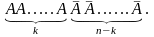
Ураховуючи незалежність подій, маємо
Р (В1) = pk q n-k (q = 1 – p ).
Кількість
варіантів, в яких А настає k
разів, а не настає n
–k разів, становить
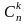 .
На основі теореми додавання ймовірностей
маємо формулу Бернуллі
.
На основі теореми додавання ймовірностей
маємо формулу Бернуллі
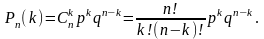
Приклад
У цеху п’ять верстатів. Ймовірність того, що кожен з них працює, p=0,8. Знайти ймовірність того, що з них працює k =0, 1, 2, 3 , 4, 5 верстатів.
Розв’язування. Згідно з формулою Бернуллі
Р5
(0) =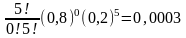 ;
Р5 (1)
=
;
Р5 (1)
=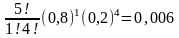 ;
;
Р5
(2) =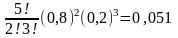 ;
Р5 (3)
=
;
Р5 (3)
=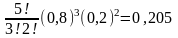 ;
;
Р5
(4) =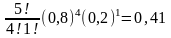 ;
Р5 (5)
=
;
Р5 (5)
= ;
;
Перевіримо,
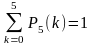 (похибка внаслідок округлення
результатів), оскільки події утворюють
повну групу.
(похибка внаслідок округлення
результатів), оскільки події утворюють
повну групу.
З цього прикладу випливає, що існує таке k = k0, якому відповідає найбільша ймовірність. Таке значення k0 називають найімовірнішим числом появи події А . Можна довести, що np – q ≤ k0 ≤ np + р
Схему Бернуллі слід відрізняти від інших аналогічних.
Приклад
У мисливця п’ять патронів . Він стріляє до першого влучення. Знайти ймовірність того, що буде витрачено k =1, 2, 3 патрони, якщо ймовірність влучення p = 0,8.
Розв’язування. Наведена схема - це не схема Бернуллі, оскільки вилучений випадок k = 0, тому формулу Бернуллі застосовувати не можна.
За умовою задачі маємо Р3 (1) = р = 0,8. Далі знаходимо
Р3
(2) =
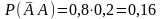 (перший патрон – промах, другий –
влучення). Нарешті,
(перший патрон – промах, другий –
влучення). Нарешті,
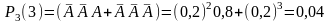
При великій кількості випробувань n формулою Бернуллі користуватися незручно. Для цих значень n є формули, за якими можна наближено обчислити ймовірність за схемою Бернуллі. Такими є формули Лапласа, які задаються відповідними теоремами (подаємо їх без доведення):
Локальна теорема Муавра-Лапласа Якщо ймовірність появи події в схемі Бернуллі дорівнює р ( р ≠ 0, р ≠ 1), а n велике, то
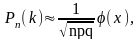
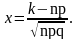
Функція
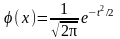 - функція Гаусса. Ця функція затабульована
(див. додатки) і має такі властивості:
- функція Гаусса. Ця функція затабульована
(див. додатки) і має такі властивості:
1.
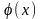 > 0 .
> 0 .
2.
— парна,
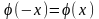 .
.
3.
max
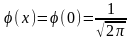
4. Вісь х =0 є асимптотою графіка ( lim = 0, х → ∞).
5. ≈ 0 при х > 4 , x < - 4, що випливає з обчислень чи з аналізу таблиці значень функції .
Приклад
Знайти імовірність того ,що з n= 100 зернин зійде рівно k = 80, якщо їх схожість р = 0,8.
Розв’язування. Згідно з формулою Лапласа, а також з таблицею , маємо
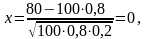
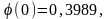
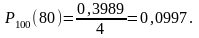
Інтегральна теорема Муавра-Лапласа Якщо ймовірність появи події в схемі Бернуллі дорівнює р ( р ≠ 0, р ≠ 1), то ймовірність того, що ця подія настане від k1 до k2 разів, дорівнює
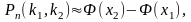
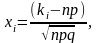 i=
1, 2 ,
i=
1, 2 ,
Функція
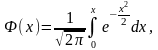 - функція
Лапласа. Ця функція затабульована (див.
додатки) і має такі властивості:
- функція
Лапласа. Ця функція затабульована (див.
додатки) і має такі властивості:
1. Ф (х) — непарна, Ф ( -х) = - Ф (х).
Ф (0) = 0.
Ф (х) зростає на ( - ∞‚ ∞ ), оскільки Ф(х) > 0.
Ф (х) ≈ 1/2 при х > 5, Ф (х) ≈ - 1/2 при х < - 5.
Приклад
Металургійний завод дістав замовлення, для виконання якого необхідно провести 90 кондиційних плавок. Ймовірність того, що плавка буде кондиційною, р = 0,9. Тому вирішили зробити n =100 плавок. Йдеться про ймовірність Р100 (90,100) , для якої ,згідно з інтегральною теоремою, маємо
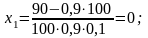

Р100 (90,100) = Ф (3,33) – Ф (0) ≈ 0,4994.
Як бачимо, дістали не таку вже й велику ймовірність.
Наступна теорема містить ще одну формулу, аналогічну формулі Бернуллі.
Формула Пуассона. Якщо в схемі випробувань Бернуллі р мале
( р< 0,1), n велике, тобто n p < 10, то
Рn (k) ≈ е- а аk / k !, а = np
