Домашнє завдання

9.1 Задано вибірку, яка характеризує місячний прибуток підприємців( у тисячах гривень). Скласти варіаційний ряд вибірки; побудувати гістограму та полігон частот.

25, 34, 38, 28, 27, 26, 30, 25, 36, 34, 35, 27, 29, 30, 35, 31, 35, 29, 30, 31.

9.2 Побудувати гістограму та полігон частот за даним розподілом вибірки

	3 – 5	5 – 7	7 – 9	9 – 11	11 – 13	13 – 15	15 – 17
mi	4	6	20	40	20	4	6

Лекція 10 Числові характеристики вибірки. Статистична функція розподілу

Аналогом функції розподілу є статистична функція розподілу:

,

де сума справа береться по усіх тих і, для яких х_і < х.

Розглянемо перший розподіл із минулої лекції.

при х -1 F* (х) = О

при -1< х 2 F* (х) = 0,05

при 2<х 5 F*(х) = 0,05+ 0,10 = 0,15

при 5<х 8 F*(х) = 0,15+ 0,40 = 0,55

при 8<х 10 F* (х) = 0,55 + 0,30 = 0,85

при х>10 F*(х) = 0,85+ 0,15 = 1

При великому об'ємі вибірки графік цієї функції дає можливість судити про теоретичну функцію розподілу F(х). Різниця між ними полягає у тому, що теоретич­на функція розподілу F(х) дорівнює Р( X < х), а статистична функція розподілу F*(х) дає частоту цієї події при експерименті. За законом великих чисел можна встанови­ти, що 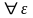>0

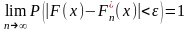
тут F_n*(х) означає статистичну функцію розподілу, одержану при п незалежних експериментах. За функцією F_n*(х) можна судити про функцію розподілу F(х).

Числові характеристики вибірки

1. Вибіркове середнє

2. Мода - значення х_і, яке має найбільшу частоту М₀Х = x_i.

3. Медіана - значення x_i , яке ділить варіаційний ряд навпіл.

4. Вибіркова дисперсія .

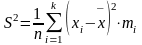Виправлена вибіркова дисперсія .

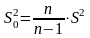5. Середнє квадратичне відхилення .

6. Коефіцієнт варіації .

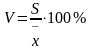7. Вибірковий коефіцієнт асиметрії .

8. Вибірковий коефіцієнт ексцесу

Е .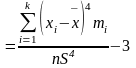

Домашнє завдання

1. Задано вибірку, яка характеризує місячний прибуток підприємців( у тисячах гривень). Обчислити моду, медіану, середнє арифметичне, дисперсію, коефіцієнт асиметрії та ексцесу варіаційного ряду.

25, 34, 38, 28, 27, 26, 30, 25, 36, 34, 35, 27, 29, 30, 35, 31, 35, 29, 30, 31.

2. За даним розподілом вибірки обчислити моду, медіану, вибіркове середнє, дисперсію, коефіцієнт асиметрії та ексцесу.

	3 – 5	5 – 7	7 – 9	9 – 11	11 – 13	13 – 15	15 – 17
mi	4	6	20	40	20	4	6

Лекція 11 Точкові та інтервальні оцінки параметрів розподілу.

Довірчі інтервали для параметрів нормального розподілу

Часто інженеру або досліднику треба подати інформацію про розподіл випад­кової величини через декілька параметрів, що цей розподіл описують. Навіть тоді, коли невідома формула функції або щільності розподілу, корисно обчислити головні покажчики на базі тих даних, що одержані у експерименті.

Параметри статистичного розподілу є емпіричними аналогами відповідних те­оретичних параметрів і служать їх точковими оцінками (точковою називають оцін­ку, що визначається одним числом). Для МХ оцінкою є , для DХ - S².

Точкові оцінки повинні бути незміщеними. Незміщеною називають статисти­чну оцінку ^* , якщо її математичне сподівання дорівнює оцінюваному параметру  при будь-якому об'ємі вибірки, тобто

M(^*)= ; M =MX; MS²=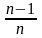 DX.

Вибіркове середнє та виправлена дисперсія , 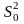- незміщені оцінки.

Незміщена оцінка може давати добре, а може і не зовсім добре наближення до оцінюваного параметра; треба щоб і дисперсія величини, що оцінюється була ма­лою.

Ефективною називають статистичну оцінку, яка при заданому об'ємі вибірки n має найменшу можливу дисперсію. Оцінки , являються ефективними.

Спроможною називають оцінку, яка при прямує по ймовірності до па­раметра, що оцінюється. Спроможність оцінок , означає, що для будь-якого

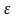>0

; .

Теорія математичної обробки даних має у своєму арсеналі два принципи оцін­ки невідомих параметрів розподілу: точкове та інтервальне оцінювання. Недолік то­чкових оцінок у тому, що невідомо, з якою точністю вони визначають шуканий па­раметр. Якщо для великого числа спостережень (об'єму вибірки) точність звичайно буває достатньою для практичних висновків (у силу незміщеності, ефективності і спроможності), то для вибірок невеликого об'єму питання про точність оцінок яв­ляється вельми істотним. Це свідчить про можливість другого підходу, зв'язаного з інтервальними оцінками.

Нехай  - шуканий параметр розподілу, а ^*- його точкова оцінка, знайдена за даними досліду. Чим менше різниця |-^*|, тим краще якість оцінки, тим точніша оцінка. Точність оцінки характеризується числом таким, що |^*--^*|< . Параметр  невідомий, тому при заданому ставиться питання лише про ймовірність події

|-^*|<

Довірчою ймовірністю або надійністю називають ймовірність виконання нерівності |-^*|< і позначають 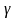, тобто

(11.1)

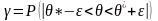
Звичайно надійність задається; часто покладають:

= 0,9; 0,95; 0,99; 0,9973.

Формула (11.1) означає, що з ймовірністю параметр  попадає у інтервал ( *- ;  *+ ). Цей інтервал називають довірчим інтервалом. Іншими словами, - ймовірність того, що інтервал покриває невідомий параметр .

Довірчий інтервал для математичного сподівання нормальної випадкової ве­личини при відомому середньому квадратичному відхиленні :

Так, як X  N (;²), то 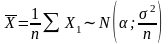. Дійсно, сума нормально розпо­ділених величин нормально розподілена і

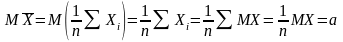, (так як всі X і мають розподіл X),

,

Якщо σ – відоме, α – невідоме, то

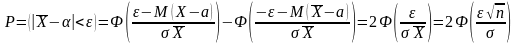
Якщо t – розв'язок рівняння 2Ф (t) = , то довірчий інтервал надійності для параметра α приймає вигляд:

Так як = t, то = , де – точність оцінки.

Довірчий інтервал для математичного сподівання нормальної випадкової ве­личини при невідомому σ має вигляд:

,

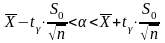де – критичні точки так званого розподілу Стьюдента з (n - 1) степенями свобо­ди, а S₀ – корінь квадратний з виправленої вибіркової дисперсії.

Довірчий інтервал для середнього квадратичного відхилення нормальної випад­кової величини.

Нехай за вибіркою об'єму n знайдена виправлена дисперсія . Тоді інтер­вал має вигляд:

(1 - q) · S₀ < σ < (1 + q) · S₀, для q < 1;

0 < σ < (1 + q) · S₀, для q > 1.

Де q – визначається за таблицею значень q = q ( , n) (див. додатки).