
- •Домашнє завдання
- •Ймовірність появи хоча б однієї події
- •Домашнє завдання
- •Домашнє завдання
- •Домашнє завдання
- •Величини та її властивості. Дискретні випадкові величини та їх розподіли
- •5. Розподіл Пуассона ( закон розподілу рідкісних подій)
- •Домашнє завдання
- •Домашнє завдання
- •Властивості математичного сподівання
- •Домашнє завдання
- •Домашнє завдання
- •Числові характеристики вибірки
- •Домашнє завдання
- •Домашнє завдання
- •Лекція 12 Поняття статистичної гіпотези. Статистичний критерій.
- •Критерій згоди Колмогорова
- •Домашнє завдання
- •Домашнє завдання
- •Домашнє завдання
Домашнє завдання
Щільність розподілу випадкової величини має вигляд
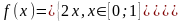 .
.
Знайти функцію розподілу F(x), обчислити P(0,6<x<0,8).
Щільність розподілу випадкової величини має вигляд
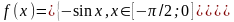 .
.
Знайти
функцію розподілу F(x),
обчислити
 .
.
Функція розподілу має вигляд
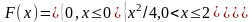 .
Знайти щільність розподілу f(х),
обчислити
.
Знайти щільність розподілу f(х),
обчислити
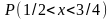 .
Побудувати графіки
f(х),
F(х).
.
Побудувати графіки
f(х),
F(х).Функція розподілу має вигляд
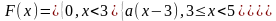 .
Знайти параметр а,
щільність розподілу f(х),
обчислити
.
Знайти параметр а,
щільність розподілу f(х),
обчислити
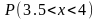 .
Побудувати графіки
f(х),
F(х).
.
Побудувати графіки
f(х),
F(х).Функція розподілу має вигляд
 . Знайти щільність розподілу f(х),
обчислити
. Знайти щільність розподілу f(х),
обчислити
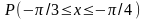 .
Побудувати графіки
f(х),
F(х).
.
Побудувати графіки
f(х),
F(х).Випадкова величина рівномірно розподілена на відрізку [2;5]. Знайти щільність розподілу f(х), функцію розподілу F(x), обчислити ймовірність попадання величини у проміжок [3;3,5].
Випадкова величина Х розподілена за нормальним законом з параметрами a=3 і σ=0,3. Знайти щільність розподілу f(х), функцію розподілу F(x), обчислити ймовірність попадання величини у проміжок [2,8;3,5].
Випадкова величина Х розподілена за експоненціальним законом з параметром λ=2. Знайти щільність розподілу f(х), функцію розподілу F(x), обчислити ймовірність попадання величини у проміжок [1,8;2,3].
Лекція 7 Числові характеристики випадкової величини
Закон, функція і щільність розподілу випадкової величини дають повну інформацію про неї. Проте дістати такі характеристики часто не просто, оскільки, як правило, необхідна велика кількість певних досліджень. Крім того, для розв’язування багатьох практичних задач можна обійтися набагато меншим обсягом інформації, а в багатьох випадках доцільним є сумарне уявлення про випадкову величину. Через те в теорії ймовірностей широке застосування набули так звані числові характеристики випадкових величин, основні з яких – математичне сподівання та дисперсія.
Означення Математичним сподіванням випадкової величини Х називається
М
(Х) = ,
М (Х) =
,
М (Х) =
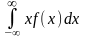 (7.1)
(7.1)
відповідно
для дискретних і неперервних величин,
тут хі
– значення величини, рі
– ймовірність цих значень,
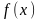 - щільність імовірності величини.
- щільність імовірності величини.
Математичне сподівання характеризує середнє значення випадкової величини і зберігає її розмірність. Математичне сподівання є аналогією центра мас систем матеріальних точок.
Властивості математичного сподівання
М (С) = С.
Справді, розглядаючи сталу як випадкову величину, яка набуває єдиного значення з імовірністю, яка дорівнює одиниці, маємо М (С) = С·1 = С.
М (ХY) = М (Х) М (Y) для незалежних Х і Y.
Н а с л і д о к 1. М (СХ) = СМ (Х).
Н а с л і д о к 2. М (Х – М (Х)) = 0.
Справді М (Х - М (Х))= М (Х) – М (М (Х))= М (Х) – М (Х) = 0.
Приклад
Знайти М (Х), якщо Х розподілена за біноміальним законом, тобто Х є кількістю появ деякої події при n випробуваннях за умови, що ймовірність появи події в кожному випробуванні дорівнює р. Нехай Хі – кількість появ події в і-му випробуванні. Значення Хі – це 0 або 1, ймовірності q і р, отже,
M (Xi) = 0 · q + 1 · p = p.
Далі знаходимо
М (Х)= М (Х1 + Х2 + . . . + Хn ) = М (Х1) + М (Х2) + . . . +. М(Хn)=np
Приклад
Знайти М (Х), якщо Х розподілено за законом Пуассона.
Розв’язування.
Маємо

Для розподілу Пуассона М (Х) = λ (λ – параметр розподілу).
Для нормального розподілу М (Х) = а (а – параметр розподілу).
Для
експоненціального розподілу М (Х) =
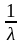 .
.
Для
рівномірного розподілу М ( Х ) =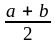 .
.
Для
геометричного
розподілу М
(Х) =
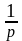 .
.
Дві випадкові величини можуть мати однакові математичні сподівання, але різне розсіяння своїх значень навколо математичних сподівань.
Наступна величина характеризує таке розсіяння.
Означення Дисперсією випадкової величини Х називається математичне сподівання квадрата відхилення цієї величини від її математичного сподівання, тобто
D ( X ) = M ( X - M ( X ))2 (7.2)
Рівність (7.2) конкретизується для дискретних і неперервних величин відповідно ( якщо інтеграл збіжний)
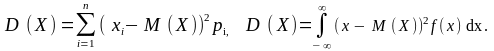
Практичне тлумачення дисперсії полягає в тому, що вона характеризує ступінь розсіяння випадкової величини навколо її математичного сподівання і вимірюється в квадратних одиницях порівняно з одиницями вимірювання вихідної величини..
Останнє приводить до введення ще однієї характеристики – середнього квадратичного відхилення, тлумачення якого таке ж, як і дисперсії, а розмір такий, як і вихідної величини, а саме:
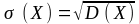
Властивості дисперсії
D ( C ) = 0.
D ( CX ) = C2 D ( X ).
D ( X ± Y ) = D ( X ) + D ( Y ), X і У - незалежні.
D ( C + X ) = D ( X ).
Кілька слів з приводу властивостей дисперсії.
Властивість 4 означає, що зміщення величини не змінює її дисперсії. Дисперсія добутку двох величин може не дорівнювати добутку дисперсій вихідних величин.
Можна
довести , що для біноміального розподілу
D (X ) = npq; для
розподілу
Пуассона D (X ) = λ. Для геометричного
розподілу D
(Х) =
 .
.
Для
рівномірного розподілу D (X) =
 ;
для експоненціального розподілу
;
для експоненціального розподілу
D
(X ) =
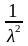 ;
для нормального розподілу D ( X ) =
;
для нормального розподілу D ( X ) =
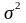 ,
де σ - параметр розподілу.
,
де σ - параметр розподілу.
Означення Початковим моментом k-го порядку випадкової величини Х називається величина
Vk = M ( X k )
Очевидно, що
v1 = M ( X ) , D ( X ) = M ( X2 ) – M2 ( X ) = v2 – v12.
Означення Центральним моментом k-го порядку випадкової величини Х називається величина
μ к = M ( X – M ( X ))k
Очевидно, що
μ 1 = M ( X – M ( X )) = 0
μ2= M ( X – M ( X ))2 = D ( X ) = v2 – v12 ,
тобто μ 2= v2 – v12 . Взагалі, довільний центральний момент можна виразити через початкові моменти, Наприклад,
μ3 = M ( X – M ( X ))3= v3 - 3v1 v2 + 2v13 ,
Означення Модою М0 (Х) розподілу випадкової величини Х називається значення Х, якому відповідає найбільша ймовірність (щільність ймовірності)
max P (X) = P (M0 ( X )) (max f (x) = f (M0 (X)).
Означення Медіаною Me (X) розподілу випадкової величини Х називається значення Х , яке задовольняє рівність
P (a < X < Me (X)) = P ( Me (X) ≤ x < b ).
Означення Асиметрією розподілу випадкової величини називається величина
As = μ 3 /σ3.
Якщо As > 0, то “довга частина” розподілу розташована справа від М (Х);
As < 0 - зліва. Асиметрія для випадкової величини, закон розподілу якої симетричний відносно М (Х) дорівнює 0.
Означення Ексцесом розподілу випадкової величини називається число
εk
=
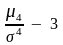
Ексцес характеризує степінь “зглаженності” ( гостровершинності) щільності розподілу в порівнянні з нормальною щільністю розподілу ( для нормального розподілу ε k = 0 )
