mls94-complete[1]

which satisfies the controllability rank condition, the norm of the optimal input is constant, that is,

ku(t)k2 = ku(0)k2 t [0, 1].

Proof. The formula for the optimal input is given in (8.13). Di erentiat-

ing it yields

u˙ i = −p˙T gi(q) − pT ∂g∂qi q˙.

Further, using the Hamiltonian equation for p˙k given by

where Ω(q, p) is a skew-symmetric matrix (i.e., it is in so(m)) given by

The solution of the linear time-varying equation (8.16) is of the form

for some U (t) SO(m) (see Exercise 6). From this fact the statement of the proposition follows.

This proposition provides an interesting formula (8.16) for the derivatives of the optimal input and establishes that the norm of the optimal input is constant. This fact can be used to establish that the same optimal input also solves other optimization problems which involve a monotone transformation of the integrand, such as

Z 1 √

uT u dt,

0

as well as some minimum-time problems (see Exercise 8). This proposition can be used to solve certain optimization problems, such as that for the so-called Engel’s system:

373

Example 8.4. Optimal inputs for Engel’s system

This system is of the form

q˙1 = u1 q˙2 = u2

q˙3 = q1u2 − q2u1 q˙4 = q12u2.

This system has growth vector (2, 3, 4). It may be verified that

0

0 [g1, g2] = 2

2q1

so that the optimal inputs satisfy the di erential equation obtained by specializing (8.16), namely

u˙ 1 = 2(p3 + q1p4)u2

(8.18)

u˙ 2 = −2(p3 + q1p4)u1.

The solution of this equation is of the form

u1(t) = r sin α(t) u2(t) = r cos α(t),

where r2 = u21(0) + u22(0). Further, since the optimal Hamiltonian given

by

H (q, p) = −12 (p1 − q2p3)2 − 12 (p2 + q1p3 + q12p4)2

is independent of q3 and q4, it follows that p˙3 = p˙4 = 0 so that p3 and p4 are constant. Using the functional form of u1 and u2 in (8.18) we get

α¨ = 2p4r sin α.

To integrate this equation, multiply both sides by 2α˙ , integrate and define

δ = 2p4r to get

(α˙ )2 = b − 2δ cos α,

where b is a constant of the integration. If b − 2|δ| > 0, this equation can

be written as

r

α˙ = ±√b − 2δ cos α = c 1 − k sin2( α2 ),

for some constants c, k. This last equation may be integrated using elliptical integrals (see, for example, Lawden [56]) for α using

374

The left hand side of this equation is an elliptic integral. Hence the optimal inputs for the Engel’s system come from elliptic functions.

In general, it is di cult to find the solution to the least squares optimal control problem for steering the system from an initial to a final point. However, it may be possible to find an approximate solution to the problem by using the so-called Ritz approximation method. To explain what this means, we begin by choosing an orthonormal basis for L2[0, 1], the set of square integrable functions on [0, 1]. One basis is a set of trigonometric functions {ψ0(t), ψ1(t), . . .} given by ψ0(t) ≡ 1 and for k ≥ 1,

For a choice of integer N , a Ritz approximation to the optimal ith input is assumed to be of the form

N

X

ui(t) = αikψk(t).

k=0

The plan now is to apply this input to steer the system

from q(0) = q0 to q(1) = qf and to determine the coe cient vectors, αi = (αi0, αi1, . . . , αiN ) RN +1 for i = 1, . . . , m, so as to minimize the cost function

In equation (8.21) the coe cient γ > 0 is a penalty term corresponding to reaching the final state. For large γ the cost function weights the reaching of the goal heavily. The heart of the Ritz approximation procedure is the hope that for large N and large γ, we will find a u that steers to the final point qf with low cost.

At this point, we have a finite-dimensional optimization problem, which may be solved by a variety of methods. One method involving a modification of the Newton iteration for minimizing J has been explored in [32] and [33], where a software package called NMPack for this purpose is described. We refer the reader to these papers for details of its application to various examples.

3.4Steering with piecewise constant inputs

In this section, we describe the rudiments of a method for motion planning for general nonholonomic systems due to La erriere and Sussmann [54].

375

The algorithm works for systems whose controllability Lie algebra is nilpotent of order k. By way of review, this means that for systems of the form

x˙ = g1u1 + · · · + gmum

the Lie products between control vector fields of order greater than k are

0; i.e., [gi1 , . . . , [gip−1 , gip ] . . .] is zero when p > k. The method proposed in [54] is conceptually straightforward but the details of their method are

somewhat involved. The first step is to derive a “canonical system equation” associated with the given control system. The chief new concept involved is that of formal power series in vector fields.

Recall from Section 2 of Chapter 7 that the flow associated with a vector field gi was denoted φgt i (q), referring to the solution of the di erential equation q˙ = gi(q) at time t starting from q at time 0. This flow is referred to as the formal exponential of gi and is denoted

etgi (q) := φgt i (q).

The usage of the formal exponential is in that we will actually use identities of the form

etgi = (I + tgi + t2 g2 + · · · ),

2! i

where polynomials like gi2 and gi3 need to be carefully justified. We will defer this question for the moment and think formally of etgi (q) as a di eomorphism from Rn to Rn. Now, consider a nilpotent Lie algebra of order k generated by the vector fields g1, . . . , gm. Recall from Section 4 of Chapter 7 that a Philip Hall basis is a basis for the controllability Lie algebra which has been constructed in such a way as to keep track of skew-symmetry and the Jacobi identity associated with the Lie bracket. We define the Philip Hall basis of the controllability Lie algebra generated

by g1, . . . , gm to be

B1, B2, . . . , Bs.

Thus, basis elements are Lie products of order less than or equal to k. In our language of formal power series, we will refer, for instance, to

:= g1g2 − g2g1

[g1, [g2, g3]] := g1g2g3 − g1g3g2 − g2g3g1 + g3g2g1.

It is a basic result of nonlinear control, called the Chen-Fliess series formula, that all flows of the nonlinear control system (8.1), namely,

m

X

376

for some suitably chosen functions h1, h2, . . . , hs, known as the Philip Hall coordinates. The meaning of equation (8.22) is as follows: all flows that could possibly be generated by the control system of (8.1) may be obtained by composing flows along the Philip Hall basis elements B1, . . . , Bs. This result bears more than a passing resemblance to the product of exponentials formula for manipulator kinematics, but we will not digress to make this connection more explicit here. Furthermore, St(q) satisfies a di erential equation involving the basis elements, namely,

where St(q) has been replaced by S(t) and the inputs v1, . . . , vs are the “fictitious inputs” corresponding to the directions of the Philip Hall basis elements B1, . . . , Bs. We say fictitious since only the first m of the Philip Hall basis elements correspond to g1, . . . , gm. The other inputs correspond to Lie bracket elements and will eventually be dropped. Differentiating equation (8.22) yields

j=1

Here, in analogy with the formulas of Chapter 2, we have introduced the

notation

Ade−hi Bi Bj = e−hi Bi Bj ehi Bi .

Since the controllability Lie algebra is nilpotent of degree k, we can express each one of the elements on the right hand side in terms of the basis elements B1, . . . , Bs. More specifically, it may be verified that

Thus each element on the right hand side of (8.24) is a linear combination of B1, . . . , Bs and we may express

for some polynomials pj,k(h). Using this in the equation (8.23) and equating coe cients of the basis elements Bi yields

377

which is a control system in Rs, called the Chen-Fliess-Sussmann equation, specifying the evolution of the Philip Hall coordinates in response to the “fictitious inputs” v1, . . . , vs. It is important to realize that, in general, the dimension s of the Philip Hall coordinates is greater than n, the dimension of the state space of the control system. The initial conditions are hi(0) = 0 corresponding to the identity di eomorphism at t = 0. This equation is the canonical form associated with the nilpotent controllability Lie algebra associated with the given problem.

Example 8.5. Nilpotent system of degree three with two inputs

Consider a two-input system which is nilpotent of degree three on R4. We will assume that g1, g2, [g1, g2], [g1, [g1, g2]] are linearly independent. As the Philip Hall basis, we have

B1 = g1 B2 = g2 B3 = [g1, g2]

B4 = [g1, [g1, g2]] B5 = [g2, [g1, g2]].

Since [g2, [g1, g2]] = B5 is dependent on B1, B2, B3, B4 by hypothesis, we have in (8.23) that v5 ≡ 0. An easy calculation shows that the coe cients

Equating the coe cients of the Bi to vi with v5 = 0, we get the Chen- Fliess-Sussmann equation

378

Note that this system is in R5, though the state space equations evolve on R4.

Example 8.6. Two-input, five-state chained system

Consider a chained system with two inputs and five states, where the input vector fields are

The system is nilpotent of degree k = 4, and the Philip Hall basis vectors are

The vector fields g1, g2, g3 := adg1 g2, g4 := ad2g1 g2, and g6 := ad3g1 g2 span the tangent space of R5.

Thus, for the Chen-Fliess-Sussmann equations, we have v5 = v7 =

The calculations for the remaining terms are carried out in a similar fashion and the results are given below (we invite the reader to do the

379

with initial condition h(0) = 0.

The task of steering the system from q0 to qf still remains to be done. This is accomplished by choosing any trajectory connecting q0 to qf indexed by time t. This is substituted into (8.23) to get the expression for the “fictitious inputs” v1, . . . , vn, corresponding to the first n linearly independent vector fields in the Philip Hall basis of the control system. The inputs vi are said to be fictitious, since they need to be generated by using the “real” inputs ui, i = 1, . . . , m. To do so involves a generalization of the definition of Lie brackets given in Section 2 of Chapter 7. For instance, to try to generate an input v3 corresponding to [g1, g2] in the previous example, one follows the definition and uses the concatenation of four segments, each for √ǫ seconds: u1 = 1, u2 = 0; u1 = 0, u2 = 1; u1 = −1, u2 = 0; u1 = 0, u2 = −1. The resulting flow is given by

380

A formula called the Campbell-Baker-Hausdor formula gives an expression for this in terms of the Philip Hall basis elements. We will make a brief digression to state this formula, since it is important in its own right (the proof and a more exhaustive recursive formulation of the coe cients is given in [115]).

Theorem 8.5. Campbell-Baker-Hausdor formula

Given two smooth vector fields g1, g2 the composition of their exponentials is given by

eg1 eg2 = eg1 + g2 + 12 [g1, g2] + 121 ([g1, [g1, g2]] − [g2, [g1, g2]]) · · · (8.29)

where the remaining terms may be found by equating terms in the (noncommutative) formal power series on the rightand left-hand sides.

Using the Campbell-Baker-Hausdor formula for the flow in equation (8.28) gives the Philip Hall coordinates to be

h = (0, 0, ǫ, h4(ǫ)),

where h4(ǫ) is of higher order than one in ǫ. Thus, the strategy of cycling between u1 and u2 not only produces motion along the direction [g1, g2], but also along [g1, [g1, g2]]. Thus, both v3, v4 6= 0. However both the h1 and h2 variables are una ected. To generate motion along the v4

direction, one concatenates an eight-segment input consisting of cycling

√

between the u1, u2 for 3 ǫ seconds. Since the controllability Lie algebra is nilpotent, this motion does not produce any motion in any of the other bracket directions (in the context of the Campbell-Baker-Hausdor formula above, the series on the right hand side of (8.29) is finite). This example can be generalized to specify a constructive procedure for generating piecewise constant inputs for steering systems which have nilpotent controllability Lie algebras.

When the controllability Lie algebra is not nilpotent, the foregoing algorithm needs to be modified to steer the system only approximately. The two di culties in this case are:

1.The Philip Hall basis is not finite.

2.The Campbell-Baker-Hausdor formula does not terminate after finitely many terms.

One approach that has been suggested in this case is to try to change the input gi using a transformation of the inputs, that is by choosing a

matrix β Rm×m so as to make the transformed g˜i, defined by

g˜1 g˜2 · · · g˜m = β g1 g2 · · · gM

a nilpotent control system. Other approaches involve “nilpotent approximations” to the given control system. For more details on the algorithm for steering nonholonomic systems using piecewise constant inputs, see the paper of La erriere and Sussmann [54].

381

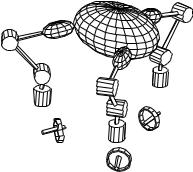
Figure 8.2: Three-fingered hand grasping an object. The small circles below each finger indicate the internal forces applied by each finger. (Figure courtesy of John Hauser)

4Dynamic Finger Repositioning

We return now to the problem of repositioning the fingers on a hand without actually lifting the fingers from the object. As we saw in the examples in Section 4 of Chapter 7, if we have spherical fingertips contacting a planar face, it is possible to move the contact point via pure rolling. This section works out this problem in detail and gives several di erent solutions for the dynamic finger repositioning problem.

4.1Problem description

Consider the grasping control problem with rolling contacts, such as the system shown in Figure 8.2. In Chapter 5, we derived the kinematic equations of motion for a single body in contact with a set of fingers. In local coordinates, the overall constraints on the system have the form

where θ is the vector of finger joint angles and x specifies the position and orientation of the grasped object.

If the grasp described by the constraints in equation (8.30) is manipulable, then any object velocity x˙ can be accommodated by some finger

that the null space of Jh is nontrivial. This situation corresponds to the existence of internal motions of the fingers that do not a ect the motion of the object. If we let u1 be an input which controls the velocity of the object and let u2 parameterize the internal motions, then equation (8.30)

382