0. Первая матрица инциденций «узлы-ветви» и ее применение для записи 1-го закона Кирхгофа

Для составления первой матрицы инциденций [M]_nxmзаготавливается таблица, состоящая изnстрок (по числу узлов) иmстолбцов (по числу ветвей), гдеm=n+k. Строки ее соответствуют узлам, а столбцы ‑ ветвям схемы замещения.

Номер строки матрицы соответствует номеру рассматриваемого узла i. Номер столбцаjсоответствует номеру рассматриваемой ветви в объединенном массиве информации о ветвях.

Элемент матрицы М_i,j, принадлежащий i-й строке и j-ому столбцу, может принимать одно из трех значений ±1 или 0:

М_i,j= 1 -если узел i является начальной вершиной ветви j (ветвь j “оттекает” от узла i).

M_i,j = ‑1 -если узел i является конечной вершиной ветви j (ветвь j “подтекает” к узлу i).

М_i,j = 0-если узел i не является вершиной ветви j, т.е. не связан с этой ветвью.

Правило знаков о направлениях подтекающих и оттекающих ветвей и задающих нагрузочных и генерирующих токов (мощностей) можно принять любое, но единое в рамках решаемой задачи.

Каждая i-я строка матрицы [М] показывает, какие ветви j связаны с данным узлом i и как они направлены. Если ввести в рассмотрение вектор-столбец токов ветвей [I]

[I]=[ I_1, I_2, I_{3, …,}I_m] ,

то произведение i-й строки матрицы [М] на вектор-столбец токов ветвей [I], полученное по правилам действий с матрицами, даст алгебраическую сумму токов, сходящихся по ветвям в i-том узле, и эта сумма должна быть равна задающему току в узле J_уi, т.е. получаем выражение 1-го закона Кирхгофа для соответствующего узла i

(1)

Если такое умножение выполнить для всех строк матрицы [М], то получим запись первого закона Кирхгофа для схемы в целом:

[M] [I] = -[J_у] (2) где [J_у] = [ J_{1 ,} J_{2 ,} J_{3 , …,} J_n ] – вектор-столбец задающих токов вnнезависимых узлах (БУ не является независимым узлом).

1-я матрица инциденций М, дополненная строкой для балансирующего узла M_n+1,j, гдеj= 1,…,m, обозначается какM_∑. Каждыйj-ый столбец матрицыM_∑ содержит обязательно +1 и -1 и указывает, какие узлы ограничиваю даннуюj-ую ветвь.

Сумма элементов любого j-го столбца матрицыM_∑равна нулю.

Знаки для элементов вектор-столбцов токов ветвей [I] и токов узлов [J], входящих в состав выражения (1) и (2), принимаются, как и для элементов матрицы [М]. Следовательно, токи нагрузок стоящие в вектор-столбце J_у, оттекают от узлов и имеют знак «+», токи генераторов подтекают к узлам и имеют знак «-».

При принятой раздельной нумерации ветвей дерева и хорд, матрица [М] формируется как блочная с блоком М_αразмерностью (nxn) ‑ для дерева сети, и блоком М_размерностью (nxk) – для хорд -. Соответственно вектора параметров ветвей и параметров режима ветвей будут содержать составляющие для дерева сети (Z_α,I_α,S_α), и для хорд (Z_,I_,S_).

;.

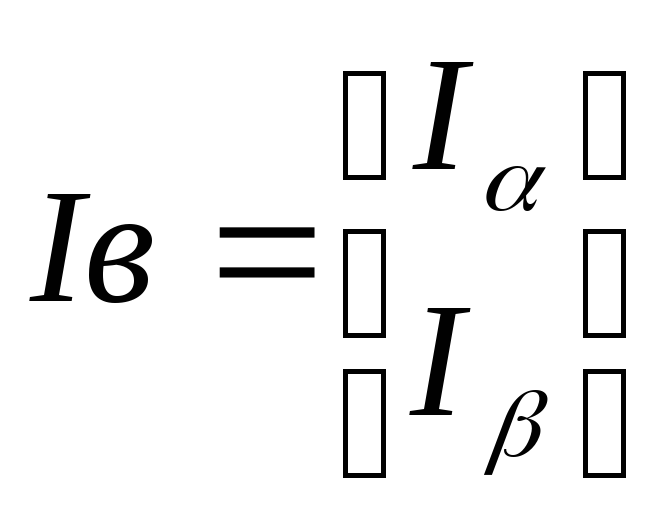С учетом блочной структуры матриц выражение (2) примет вид

(3)

Выполнив умножение, получим:

М_α I_α + М_ I_ = ‑J (4)

Для схемы типа дерева – разомкнутой сети, М_= 0,I_= 0. Тогда выражение (4) примет вид

[M_][I_] = ‑[J]. (5)

Подматрица М_αквадратная, невырожденная, сумма ее строк не обращается в ноль. Следовательно, уравнение (5) может быть решено относительно токов в ветвях дереваI_α

[I_] = ‑[M_]^-1 [J] (6)

Обратную матрицу [М_]^-1можно находить прямым обращением матрицы для дерева сети М_, но можно определить путем элементарных преобразований матрицы М_. К элементарным преобразованиям относятся:

- перестановка строк.

- умножение всех элементов строк на число не равное нулю.

- прибавление к строке другой строки, умноженной на некоторое число.

Схематически процесс нахождения обратной матрицы можно изобразить так:

[M_αE]элементарные преобразования[EС_р]

Здесь [C_p] = [М_]^-1– матрица, обратная матрице [М_] – представляет собой матрицу коэффициентов токораспределения для дерева сети; согласно (6) ее элемент С_{р ij}показывает, будет ли протекать токj-ого узла поi-ой ветви дерева схемы.

В частном случае разомкнутой сети типа дерева по уравнению (6), с помощью матрицы [С_р] при известных задающих токах узлов [J_у] может быть найдено токораспределение в ветвях – матрица [I_]:

[I_] = ‑ [C_p][J] (7)

В разомкнутом режиме по схемам типа дерева работает целый класс электрических сетей – распределительные сети с номинальными напряжениями 0,4 кВ, 6-10 кВ, 35кВ, частично 110 кВ, которые выполнены (сооружены) как замкнутые сети с резервированием, но работают в разомкнутом режиме. Поэтому быстрые и эффективные способы решения на ЭВМ задачи (6) (7) практически актуальны.Они были разработаны и программно реализованы в 70-х годах в работах кафедры электрических сетей и систем Киевского политехнического института, Белорусского политехнического института и явились основой алгоритмов оптимизации режимов разомкнутых сетей – например, поиск оптимальных мест размыкания городской кабельной сети по критерию минимума потерь мощности и энергии.