
- •Министерство образования республики беларусь
- •Удк 621.311
- •Содержание
- •1.1 Понятие о режимах электрических систем и схемах замещения 5
- •Уравнения установившихся режимов электрических систем
- •1.1 Понятие о режимах электрических систем и схемах замещения
- •1.2 Аналитическое представление информации о конфигурации электрической сети с помощью матриц инциденций и матричное выражение законов Кирхгофа
- •Первая матрица инциденций «узлы-ветви» и ее применение для записи 1-го закона Кирхгофа
- •Вопросы для самопроверки:
- •1.2.2 Вторая матрица инциденций «ветви-контуры» и матричная запись второго закона Кирхгофа
- •1.2.3 Запись уравнений состояния сети по законам Кирхгофа
- •1.3 Метод уравнений узловых напряжений
- •1.3.1 Вывод узловых уравнений
- •Здесь [м]т – транспонированная 1-я матрица инциденций,
- •1.3.2 Определение матрицы узловых проводимостей и ее характеристика
- •1.4 Контурные уравнения установившихся режимов электрических систем
- •Запись уравнений состояния сети с помощью матриц обобщенных параметров.
- •Вопросы для самопроверки
- •1.6 Расчёт режима электрической сети с использованием матрицы коэффициентов распределения
- •Расчётные токи в узлах сети можно определить как:
- •2. Методы решения уравнений установившихся режимов электрических систем
- •2.1 Итерационные методы решения систем уравнений
- •2.2 Критерии сходимости итерации и анализ их выполнения для узловых уравнений установившихся режимов
- •2.2.1 Теорема сходимости итерации
- •2.2.2 Факторы, влияющие на сходимость итерации для узловых уравнений установившихся режимов
- •2.2.3 Критерии и анализ сходимости итерации для нелинейных систем узловых уравнений установившихся режимов
- •2.3 Решение уравнений узловых напряжений итерационными методами
- •2.3.1 Решение уравнений узловых напряжений в форме баланса токов
- •2.3.2 Обращенная форма уравнений узловых напряжений и их анализ
- •2.4 Применение метода Ньютона для решениядля нахождения корней уравнений установившихся режимов
- •2.4.1 Обоснование метода Ньютона для решения нелинейного уравнения
- •2.4.2 Применение метода Ньютона для систем нелинейных уравнений
- •2.4.3 Решение нелинейных узловых уравнений методом Ньютона.
- •III. Задание на курсовую работу
- •Содержание расчетно-пояснительной записки (перечень подлежащих разработке вопросов)
- •Перечень графического материала (в виде компьютерных рисунков в формате а4)
- •IV. Примеры для выполнения разделов курсовой работы
- •С бУоставляем граф-схему замещения электрической сети и нумеруем её ветви и узлы (ребра и вершины) в соответствии с принципом ярусности:
- •Составление элементарных матриц параметров режима [pу], параметров сети [dZв],[dYв] и матриц соединений [м] и [n].
- •Расчёт матрицы узловых проводимостей [Yy] и матрицы контурных сопротивлений [Zk].
- •Расчет режима электрической сети по узловым уравнениям путем обращения матрицы узловых проводимостей
- •Расчет режима электрической сети на основе линейных контурных уравнений
- •Решение нелинейных обращенных узловых уравнений с матрицей- методом простой итерации.
- •Пример расчета:
- •Пример расчета:
- •Заключение Литература
Пример расчета:
1 4 VII
![]()







I VI 3

![]()
IV
5 БУ 1 2
![]()

![]()
V





3![]()
II III

2
![]()
В выражении (15) учтем узловые мощности с их знаками (Pн < 0,Pг > 0), получим матрицу Якоби для схемы рис.
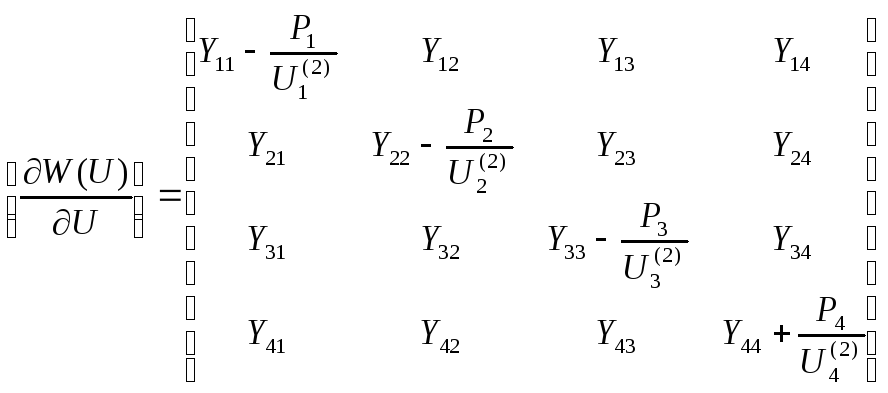
Зададимся начальным приближением.
Обозначим:
![]() и
и
![]()
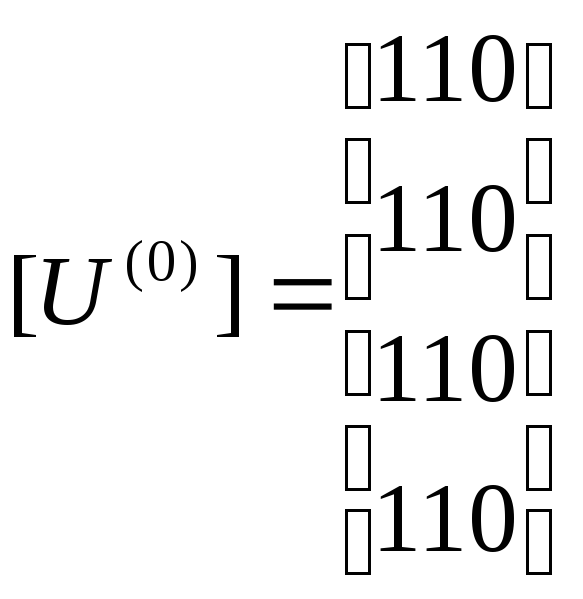
Первая итерация:

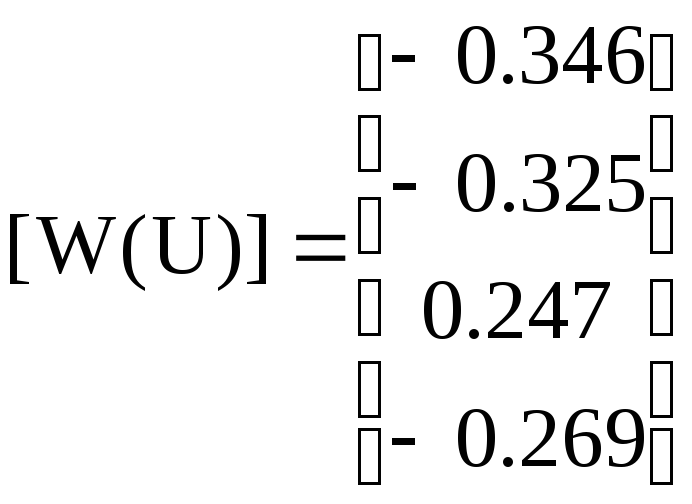

Обратная матрице [V]

Подставив данные, получим поправку к напряжениям в узлах на первой итерации
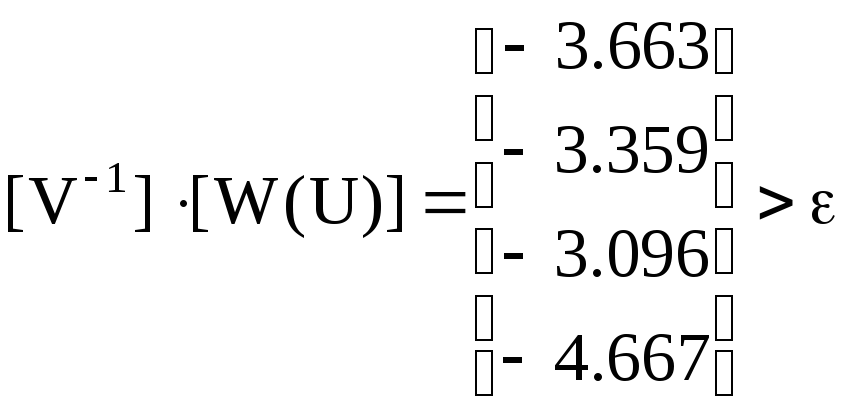 ,
,
![]()
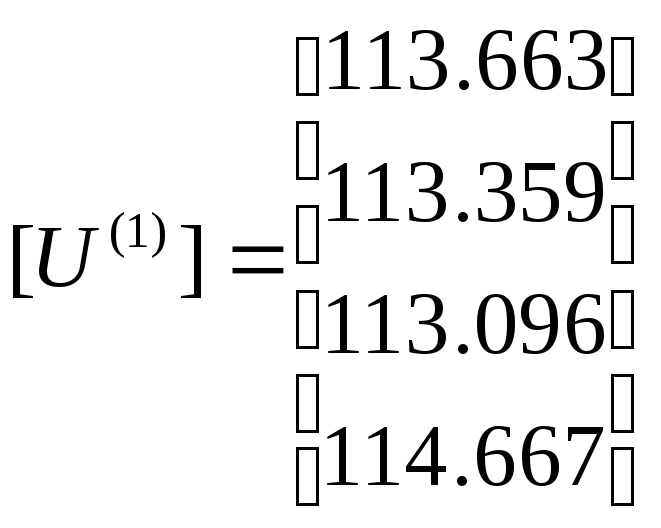 (кВ).
(кВ).
Вторая итерация:


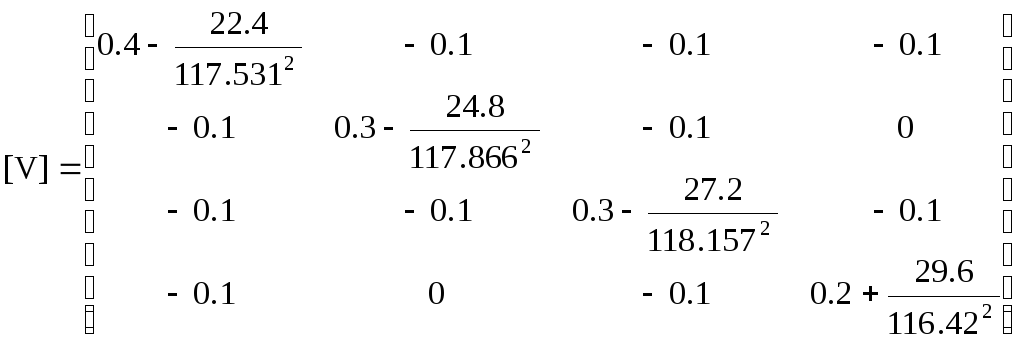
Обратная матрице [V]

Итерационный процесс закончен!
После нахождения напряжений в узлах определяем параметры режима ветвей электрической сети.
Расчет режима электрической сети.
1. Определяются падения напряжение в узлах относительно напряжения в балансирующем узле:
![]() , (19)
, (19)
где
![]() —напряжения в узлах;
—напряжения в узлах;
n— единичная матрица-столбец.
2. Определяются токи ветвей:
![]() , (20)
, (20)
где
![]() —диагональная
матрица проводимостей ветвей;
—диагональная
матрица проводимостей ветвей;
![]() —транспонированная
матрица инциденций.
—транспонированная
матрица инциденций.
3. Определяются падения напряжения на ветвях схемы:
![]() (21)
(21)
4. Определяются потоки мощности в ветвях:
![]() , (22)
, (22)
5. Определяются потери мощности в ветвях:
![]() . (23)
. (23)
6. Определяются суммарные потери мощности в сети:
![]() . (24)
. (24)
7. Определяются расчетные токи узлов:
![]() . (25)
. (25)
8. Определяются расчетные мощности в узлах:
![]() , (26)
, (26)
где
![]() —диагональная
матрица напряжений в узлах.
—диагональная
матрица напряжений в узлах.
9. Для каждого узла определяется небаланс по мощности:
![]() , (27)
, (27)
и в %:
![]() , (28)
, (28)
где
![]() —рассчитанная
мощность,
—рассчитанная
мощность,
![]() —
заданная мощность.
—
заданная мощность.
3.4 Расчет потокораспределения сети на основе рассчитанных узловых напряжений приведен из работы студента ….
Для автоматизации расчета потокораспределения эффективно используется разделение матрицы инциденций М++ М- =М
Рассчитаем потокораспределение в схеме и потери мощности в ветвях схемы замещения электрической сети. Для этого рассмотрим матрицу инциденций МΣ, составленную с учетом балансирующего узла, а также вектор-функцию узловых напряжений с учетом балансирующего узла:

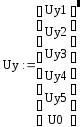
Представим матрицу
![]() в виде двух составляющих матриц - для
подтекающих оттекающих ветвей:
в виде двух составляющих матриц - для
подтекающих оттекающих ветвей:
![]() (5)
(5)
 =
= +
+
Получаем следующие соотношения:
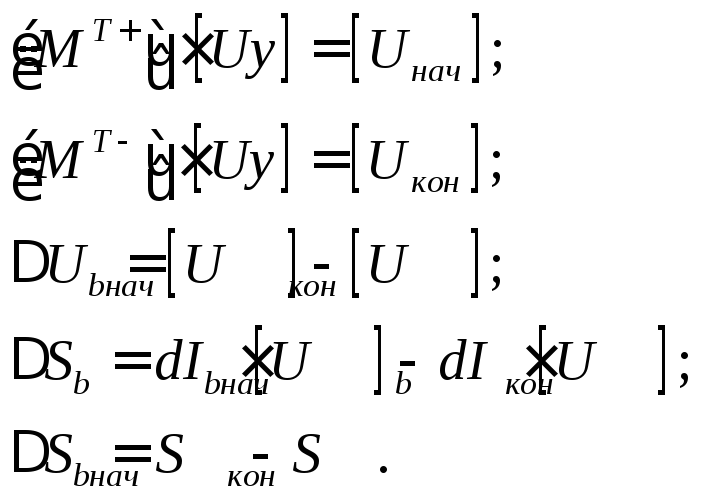
![]()
Где
![]() вектор-столбец
напряжений начал ветвей;
вектор-столбец
напряжений начал ветвей;
![]() вектор-столбец
напряжений концов ветвей;
вектор-столбец
напряжений концов ветвей;
![]() диагональная
матрица токов в ветвях схемы;
диагональная
матрица токов в ветвях схемы;
![]() вектор-столбец
потоков мощностей в началах ветвей;
вектор-столбец
потоков мощностей в началах ветвей;
![]() вектор-столбец
потоков мощностей в концах ветвей;
вектор-столбец
потоков мощностей в концах ветвей;
![]() вектор-столбец
потерь мощности в ветвях схемы.
вектор-столбец
потерь мощности в ветвях схемы.
Имеем:


Error: Reference source not found
3.5 Расчет утяжеленного режима с применением матриц обобщенных параметров электрической сети.
У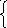 равнения
состояния электрической сети по законам
Кирхгофа:
равнения
состояния электрической сети по законам
Кирхгофа:
![]() (1)
(1)
В выражении (1) все матрицы имеют известную структуру. Представим (1) в виде матричного уравнения с составной блочной матрицей коэффициентов и составной правой частью:
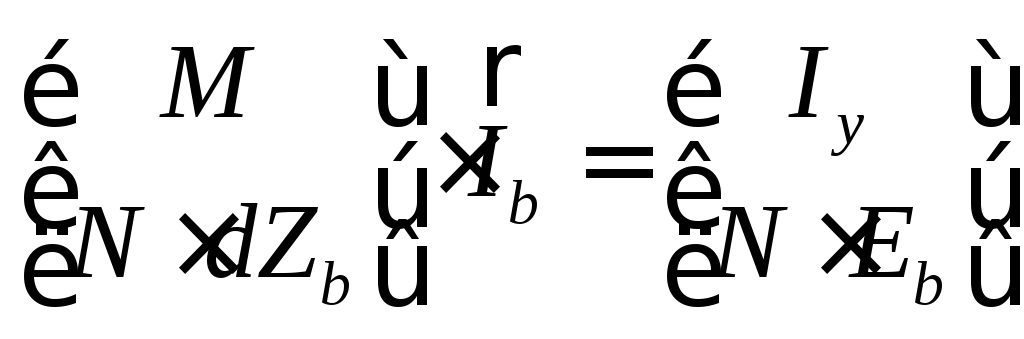 (2)
(2)
или,
приняв очевидное обозначение
![]() ,
запишем
,
запишем
![]() (3)
(3)
Здесь
![]() вектор-столбец
независимых (заданных) характеристик
режима;
вектор-столбец
независимых (заданных) характеристик
режима;
![]() искомые
токи ветвей;
искомые
токи ветвей;
![]() составная
матрица коэффициентов, содержит обе
конфигурационные модели сети MиNи параметры сетиdZb.
составная
матрица коэффициентов, содержит обе
конфигурационные модели сети MиNи параметры сетиdZb.
Система
уравнений (2), (3) имеет порядок (n+k),
равный числу ветвей схемыm.
Матрица![]() квадратная, блочная, в общем случае
невырожденная, обратную к ней матрицу
квадратная, блочная, в общем случае
невырожденная, обратную к ней матрицу![]() также представим в виде блоков:
также представим в виде блоков:
![]() (4)
(4)
Тогда токи ветвей из (3) выразятся
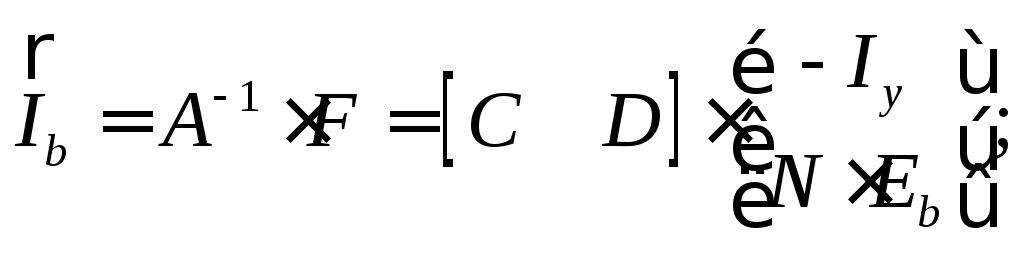 (5)
(5)
 (6)
(6)
Обозначим
произведение
![]() черезY–матрицу
проводимостей.
черезY–матрицу
проводимостей.
Тогда
![]() (7)
(7)
Выражение (7) позволяет получить токораспределение в схеме с помощью матриц обобщенных параметров CиY.
По
выражению (7), реализующему принцип
наложения (суперпозиции), токораспределение
в схеме представляет собой сумму двух
составляющих:
![]() обусловленной
задающими токами узлов сети; и
обусловленной
задающими токами узлов сети; и![]() обусловленной
наличием ЭДС в ветвях схемы. Особенность
ситуации состоит в том, что в электрических
сетях режим задают чаще всего узловыми
токамиIyили мощностямиSy,
а ЭДС в ветвях отсутствуют. Тогда
уравнение (7) получает вид:
обусловленной
наличием ЭДС в ветвях схемы. Особенность
ситуации состоит в том, что в электрических
сетях режим задают чаще всего узловыми
токамиIyили мощностямиSy,
а ЭДС в ветвях отсутствуют. Тогда
уравнение (7) получает вид:
![]() (8)
(8)
Мы получаем частный случай уравнения состояния, где С –матрица коэффициентов распределения. Матрица коэффициентов распределения С прямоугольная. Ее элемент Cijпоказывает долю токаj–того узла, протекающего поi–ой ветви.
При использовании матрицы обобщенных параметров в расчете утяжеленного режима, задаются точностью расчета ε, проводят итерационный процесс относительно задающих мощностей в узлах, итерационный процесс заканчивают, когда выполняется условие
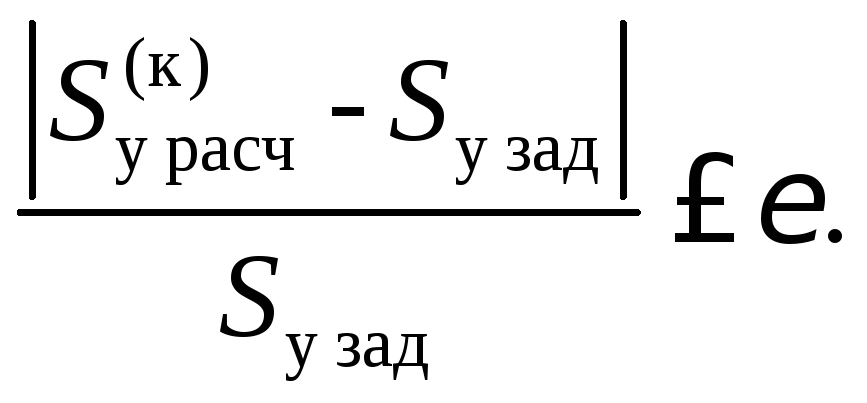 (9)
(9)
Где к –номер итерации.
Примем,
что![]() .
.
Рассчитаем матрицу обобщенных параметров:
![]() ,
(10)
,
(10)

По формуле (8) найдем токи в ветвях в первом приближении:

Где матрица задающих токов в узлах имеет вид:

Далее рассчитаем падения напряжения в ветвях сети, напряжения в узлах сети и мощности в узлах сети:



Точность расчета равна:

Полученная точность нас не удовлетворяет, поэтому продолжаем итерационный процесс.
По формуле (8) найдем токи в ветвях во втором приближении:

Где матрица задающих токов в узлах имеет вид:

Далее рассчитаем падения напряжения в ветвях сети, напряжения в узлах сети и мощности в узлах сети:



Точность расчета равна:

Полученная точность нас не удовлетворяет, поэтому продолжаем итерационный процесс.
По формуле (8) найдем токи в ветвях в третьем приближении:

Где матрица задающих токов в узлах имеет вид:

Далее рассчитаем падения напряжения в ветвях сети, напряжения в узлах сети и мощности в узлах сети:



Точность расчета равна:
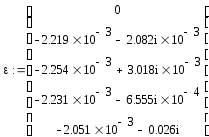
Полученная точность нас удовлетворяет, считаем итерационный процесс завершенным.
Рассчитаем потокораспределение в схеме и потери мощности в ветвях схемы замещения электрической сети. Для этого рассмотрим матрицу инциденций М, составленную с учетом балансирующего узла, а также вектор-функцию узловых напряжений с учетом балансирующего узла:


Рассмотрим матрицу
![]() и представим ее в виде двух составляющих
матриц:
и представим ее в виде двух составляющих
матриц:
![]() (11)
(11)
 =
= +
+
Получаем следующие соотношения:
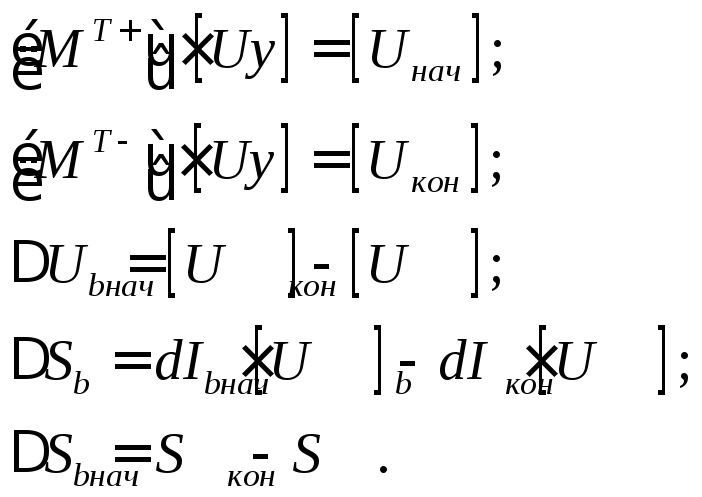
![]()
Где
![]() напряжение
в начале ветви;
напряжение
в начале ветви;
![]() напряжение
в конце ветви;
напряжение
в конце ветви;
![]() диагональная
матрица токов в ветвях схемы;
диагональная
матрица токов в ветвях схемы;
![]() поток мощности в
начале ветви;
поток мощности в
начале ветви;
![]() поток мощности в
конце ветви;
поток мощности в
конце ветви;
![]() потери
мощности в ветвях схемы.
потери
мощности в ветвях схемы.
Имеем:


Результаты расчета утяжеленного режима представлены на рис.7:
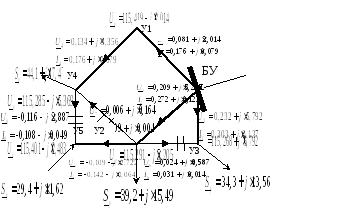
Рисунок 7.
3.6 Расчет режима по исходным узловым уравнениям в форме баланса токов при их решении методом простой итерации.
Непосредственно определить матрицы узловых напряжений можно на основании узлового уравнения в форме, требующей вычисление обратной матрицы узловых проводимостей. При расчетах сложных сетей с большим числом узлов обращение матриц высокого порядка может вызвать значительные затруднения. Применяя метод итераций, можно упростить решение узлового уравнения, при этом оно записывается в форме, не предусматривающей вычисления обратной матрицы:
![]() (25)
(25)
Матричные уравнения (13) по своей структуре полностью идентичны уравнениям, записанным в форме, использующей обратную матрицу узловых проводимостей. В левой части выражения (13) имеется произведение квадратной матрицы комплексных коэффициентов на столбцевую матрицу искомых величин, правая часть содержит известные величины.
Матричное узловое уравнение (13) в раскрытой форме будет иметь вид:
 (26)
(26)
Матричному уравнению (14) отвечает следующая система алгебраических уравнений:
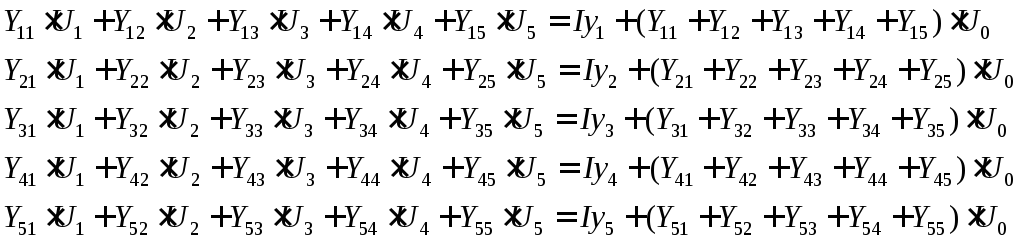
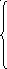 (27)
(27)
П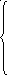 ри
произвольно принятых напряжениях в
нулевой итерации
ри
произвольно принятых напряжениях в
нулевой итерации![]() каждое из уравнений системы (15) может
быть удовлетворено, если в левую часть
их будет внесена некоторая поправка.
Рассматриваемый способ простой итерации
предусматривает внесение таких поправок
лишь к одному из неизвестных, входящих
в уравнение. При этом
каждое из уравнений системы (15) может
быть удовлетворено, если в левую часть
их будет внесена некоторая поправка.
Рассматриваемый способ простой итерации
предусматривает внесение таких поправок
лишь к одному из неизвестных, входящих
в уравнение. При этом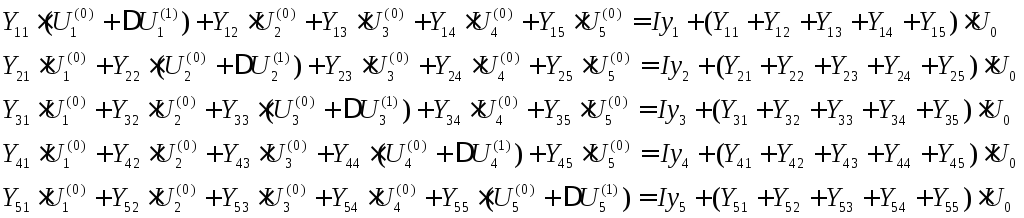 (28
(28
откуда, рассматривая
поправки
![]() в качестве неизвестных, можно найти
в качестве неизвестных, можно найти
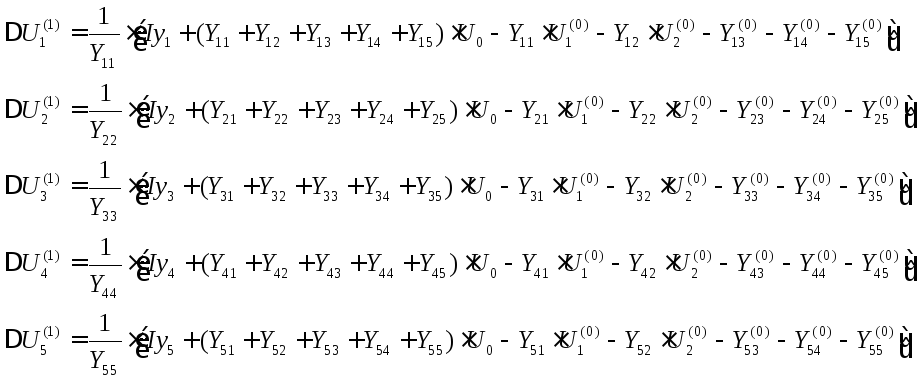
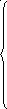 (29)
(29)
Нетрудно видеть,
что совокупность поправок, входящих в
левые части уравнений системы (17),
образует столбцевую матрицу
![]() .
Эти поправки, найденные в соответствии
с (17), позволяют удовлетворить каждое
из узловых уравнений, входящих в систему
(15). При введении этих поправок узловые
напряжения
.
Эти поправки, найденные в соответствии
с (17), позволяют удовлетворить каждое
из узловых уравнений, входящих в систему
(15). При введении этих поправок узловые
напряжения
![]() (30)
(30)
Однако эти напряжения не удовлетворяют всей системе (15) в целом, поскольку каждая из поправок была найдена из условия удовлетворения лишь одного из уравнений этой системы. Поэтому необходимы дальнейшие уточнения узловых напряжений путем введения новых поправок.
Для поправок n-ой итерации можно записать:
![]() (31)
(31)
Если при переходе от одной итерации к другой матрица поправок уменьшается, то говорят, что итерационный процесс сходится. При этом на некоторой n-ой итерации определяется матрица искомых узловых напряжений, удовлетворяющая узловому уравнению с заданной точностью. Признаком этого является удовлетворение неравенства
![]()
Примем точность
расчета равную
![]()
В начальном приближении примем:

Проведем ряд итераций:





Полученная точность расчета в 23-ей итерации нас удовлетворяет, итерационный процесс считаем завершенным.
По формуле (19) найдем искомые узловые напряжения:
![]() =
=
Произведем дальнейший расчет режима:
По известным напряжениям в узлах сети рассчитаем падения напряжения в ветвях сети:

Далее по уже известным падениям напряжения в ветвях схемы определяем токи в ветвях:

Определим небаланс мощностей в узлах сети: для этого вычислим расчетные узловые токи и соответственно –расчетные мощности в узлах, и сопоставим их с задающими узловыми мощностями.
Имеем,
![]() ;
(32)
;
(32)

Отсюда получим, что


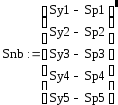

5. Особенности расчета режимов сети переменного тока с использованием пакета MathCad(выявлены студенткой Кудик Е.В.)
