2.1 Итерационные методы решения систем уравнений

В итерационных методах (или методах последовательного приближения) решение Х_*системы

AX=B(87)

получают как предел сходящейся последовательности значений

(88)

Если эта последовательность значений сходится, то разность между двумя соседними приближениями при достаточном числе итераций становится меньше заданной точности расчета _х

(89)

Здесь (89) – признак сходимости итерационного процесса.

Для применения итерационных методов необходимо выбрать вектор начального приближения X⁽⁰⁾

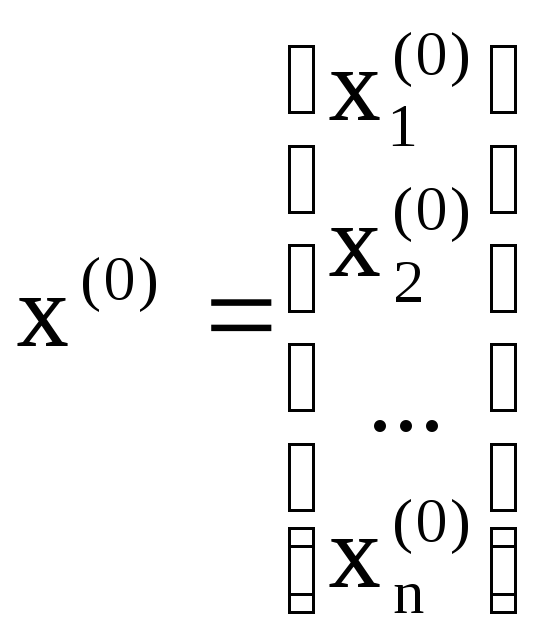
(90)

и по рекуррентному соотношению вида

(91)

организовать циклические вычисления

Х^к=( Х^к-1)

Построим рекуррентное соотношение для системы уравнений (87). Для этого разрешим уравнения системы (87), записанной в виде

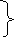a₁₁x₁ + a₁₂x₂ + … + a_1n x_n = b₁

a₂₁x₁ + a₂₂x₂ +… + a_2n x_n = b₂

_{…………………………………} (92)

a_n1x₁ + a_n2x₂ + …+ a_nnx_n = b_n

относительно диагональных неизвестных

(93)

Или в матричном виде,

x=+x(94)

Выражения (93), (94) представляют систему уравнений, подготовленную к итерации, или развернутую запись рекуррентного соотношения (91).

Итерационный вычислительный процесс по схеме (93) вида х^(к)=(х^(к-1)) ведет к решению (88)

х_*=limх^(к),

^к

если выполняются условия сходимости итерации.

2.2 Критерии сходимости итерации и анализ их выполнения для узловых уравнений установившихся режимов

2.2.1 Теорема сходимости итерации

Итерационные процессы – это численные методы решения уравнений, и их эффективность зависит от числовой характеристики матриц коэффициентов системы уравнений. Обе числовые характеристики, упоминавшиеся в теореме о сходимости итераций, формулируют условия сходимости для матрицы системы, подготовленной к итерации, в виде (93), (94).

(95)

Для матрицы наибольшее по модулю собственное значение_max<1, а норма= 1.

Зададимся начальным приближением х⁽⁰⁾и запишем следующие 4 приближения (для выявления общих закономерностей)

(96)

Подставим х⁽¹⁾, х⁽²⁾, х⁽³⁾в выражение для х⁽⁴⁾. Получим

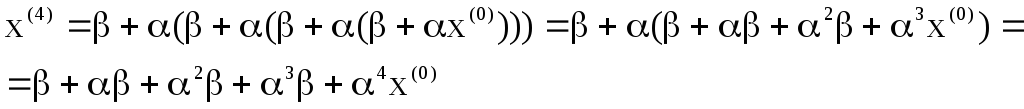(97)

Если итерационный процесс сходится, то x^(k)будет представлять собой решение системы уравнений (87), записанное как предел сходящейся последовательности значений

(97,а)

- предел сходящейся последовательности матриц, т.е. матричного степенного ряда с основанием .

Вынесем за скобку в (97).

; (98)

или в общем случае для каждого приближения

(99)

В выражении (99) скобка представляет сумму членов матричного степенного ряда, с основанием []. Этот ряд сходится ,если его сумма имеет предел; и расходится, если выполняются условия (100) или (101)

необходимое и достаточное условие сходимости (100)

достаточное условие сходимости (101)

Тогда сумма членов матричного степенного ряда определится по аналогии с суммой членов геометрической прогрессии с основанием q< 1.

Для геометрической прогрессии с числовым основанием q:

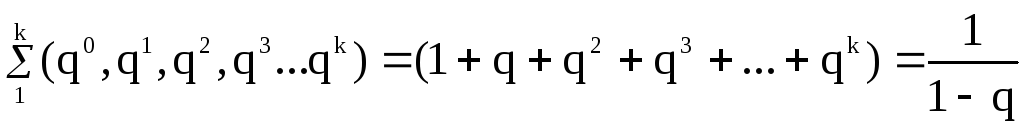
^к

Для степенного матричного ряда с основанием []:

(102)

Подставляя (102) в (99), получим

(103)

Здесь , при , или .

Тогда, домножая левую и правую части уравнения (103) на (Е - ) и учитывая, чтоlimх^(к)= х_*(k) получим

 (104)

- неподвижная точка, последовательности, или решение системы уравнений.

Выражение (104) соответствует неподвижной точке последовательности, т.е. ее пределу, когда дальнейшего изменения значения xв ходе итерационного процесса не происходит.

Достаточное условие сходимости итерации (101) и следствие из теоремы о достаточных условиях сходимости итерации позволяют получить важные заключения о соотношении диагонального и суммы побочных элементов матрицы, которое необходимо для сходимости итерационного процесса при решении уравнений.

Матрица α системы уравнения, подготовленной к итерации, имеет вид:

(106)

Применительно к узловым уравнениям установившегося режима:

(107)

(108)

Матрица системы узловых уравнений, подготовленной к итерации, имеет вид

(109)

А достаточное условие сходимости по норме запишется

(109)

и должно выполняться для всех узлов сети i= 1,2,…,n.

Неравенство (109) выражает достаточное условие сходимости итерации для системы узловых уравнений:

для всех узлов сети собственная проводимость узла Y_iiдолжна быть больше суммы модулей взаимных проводимостейY_ij. Это условиене выполняется.

Однако для тех узлов сложной схемы, которые связаны с балансирующим узлом, диагональный элемент матрицы Y, т.е. собственная проводимость узла , равен

, (110) благодаря чему для строк матрицы, которые имеют связь с балансирующим узлом

, (111) причем диагональный элемент матрицы больше суммы модулей побочных элементов именно на величину проводимости линииY_iб, которая связываетi‑й узел с балансирующим.

Благодаря выполнению соотношений (110), (111) выполняется необходимое и достаточноеусловие сходимости итерации(100), связанное не с нормой, а с собственными значениями, хотя достаточное условие сходимости по норме (101) и не выполняется.

Поэтому сходимость итерационного решения узловых уравнений имеет место, хотя и не обеспечена.