Методичні рекомендації

1. Рівняннями руху твердого тіла є другий закон Ньютона для руху центра інерції тіла і основне рівняння динаміки обертального руху. Їх застосовують для розрахунків сил і прискорень у випадку рівнозмінного руху твердого тіла (а_с = const, =const).

2. Складний рух твердого тіла зручно розглядати як суму двох рухів: обертального відносно якої-небудь осі й поступального зі швидкістю осі. Звичайно вибирають вісь обертання так, щоб вона проходила через центр інерції тіла.

3. При коченні однорідного циліндра (кулі) по площині між лінійними величинами, що характеризують рух центра інерції тіла, – швидкістю та прискоренням а_с – і кутовими величинами, що визначають обертовий рух тіла, – кутовою швидкістю і кутовим прискоренням, існують співвідношення:

,

де R – радіус циліндра (кулі).

Розв’язок типових задач

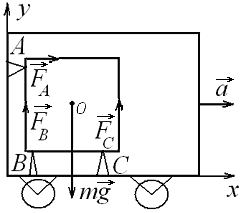
Приклад 1. Однорідний куб масою m = 10 кг лежить у вагоні на трьох опорах А, В, C (рис. 1). Визначити сили реакції опор F_a, F_b, F_c, якщо відомо, що вагон рухається з прискоренням а = 2 м/с².

Розв’язання.

Якщо куб рухається тільки поступально (), рівняння руху твердого тіла запишуться у вигляді:

a),б) (1)

Рис. 1.

На куб діють сила ,прикладена до центра куба, і три сили реакції опор, спрямованих нормально до відповідних граней куба (рис. 1). Так як ці сили в сукупності не паралельні між собою, перепишемо співвідношення (1а) у вигляді двох скалярних рівнянь, вибравши осі проекцій, як показано на рисунку. Тоді для осей Ох та Оу відповідно одержимо:

(2)

Щоб не допустити помилки, використовуючи рівняння моментів (1б), необхідно мати на увазі, що основне рівняння динаміки обертального руху, частинним випадком якого є рівняння (1б), отримане для обертання тіла навколо якої-небудь нерухомої осі, тобто для руху в інерціальній системі відліку. Однак, вибираючи яку-небудь точку тіла, що прискорено рухається, за вісь обертання й складаючи рівняння моментів відносно цієї осі, ми тим самим розглядаємо рух тіла в неінерційній системі відліку. У цьому випадку рівняння руху можна записувати, лише вводячи сили інерції. Виявляється, що, використовуючи рівняння (1б), можна все-таки не враховувати сили інерції, якщо вибрати вісь обертання, що проходить через центр інерції тіла. Дійсно, сила інерції завжди прикладена до центру інерції, тому при такому виборі осі обертання момент цієї сили дорівнює нулю.

Отже, вибравши вісь обертання, що проходить через центр інерції куба, і прийнявши позитивним напрямок обертання за годинниковою стрілкою, на підставі (1б) запишемо

, (3)

де L – довжина ребра куба. Вирішуючи систему (3), (2), знаходимо:

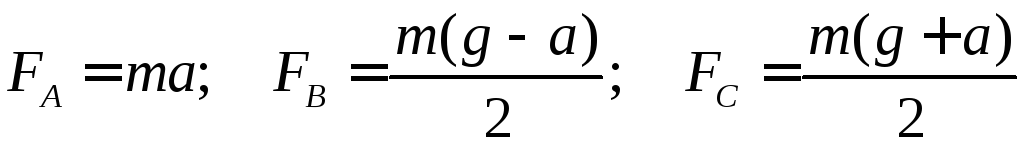
Підставивши в ці формули числові значення заданих величин і виконавши обчислення, одержимо:

.

Приклад 2. На горизонтальну вісь насаджений шків радіуса R. На шків намотаний шнур, до вільного кінця якого підвісили гирю масою m (рис. 2). Вважаючи, що маса М шківа рівномірно розподілена по ободу, визначити прискорення а, з яким буде опускатися гиря, силу натягу Т нитки й силу тиску N шківа на вісь.

Розв’язання.

Рис. 2.

Оскільки прискорення центра інерції шківа а₀ = 0 і шків тільки обертається, рівняння руху для нього запишуться у вигляді

a),б) (1)

На шків діють сили тяжіння Mg, натягу Т нитки й реакції опору на вісь N. Остання за третім законом Ньютона чисельно дорівнює шуканій силі тиску шківа на вісь. Очевидно, сила N спрямована вертикально вгору, тому що тільки в цьому випадку може виконуватися співвідно­шення (1а). Так як всі три вектори колінеарні (тобто паралельні одній і тій же прямій), рівняння (1а) можна записати в скалярному вигляді:

(2)

Шків обертається під дією лише моменту сили. Отже, використовуючи рівняння (1б), отримаємо

(3)

Момент інерції шківа, оскільки його маса розподілена по ободу, знайдемо за формулою:

(4)

Рівняння (3) і (4), що описують рух шківа, містять три невідомих: Т, N і . Для розв’язку системи, запишемо ще одне рівняння, застосувавши другий закон Ньютона для поступального руху гирі:

(5)

Оскільки шнур змотується зі шківа без просковзування, прискорення гирі дорівнює лінійному прискоренню точок на ободі шківа. Отже,

(6)

Підставивши в (3) значення I,  за формулами (4) і (5), знайдемо із системи трьох рівнянь (2), (3), (5) всі три невідомі величини:

.

Приклад 3. Система, що складається із циліндричного котка радіуса R і гирі, зв’язаних ниткою, перекинутою через блок, під дією сили тяжіння гирі починає рухатися зі стану спокою. Визначити прискорення центра інерції котка й силу натягу Т нитки. Яку швидкість набуде гиря, якщо вона опуститься з висоти h? Маса циліндра М, маса гирі m, масою блоку знехтувати. Вважати, що циліндр котиться по горизонтальній поверхні без ковзання. Тертям кочення знехтувати.

Розв’язання.

Рис. 3.

Циліндр, що котиться, приймає участь у двох рухах: обертається навколо осі й рухається поступально зі швидкістю осі. Тому скористаємося рівняннями руху твердого тіла.

На коток діють чотири сили: сила натягу T нитки, сила тяжіння Mg, сила тиску опори N і сила тертя спокою F. Остання сила зумовлена тим, що коток не сковзає, а котиться по площині, у той час як перші три сили, що проходять через вісь, не могли б викликати обертання тіла. Дія сили F не пов’язана з тертям кочення. Ця сила є складовою сили реакції опори, що протидіє виникненню ковзанню котка по площині. При зникненні сили натягу Т нитки зникає й сила F.

Так як сили Mg і N зрівноважуються (прискорення по вертикалі немає), ми їх надалі враховувати не будемо.

Можливі два подальших шляхи рішення задачі, пов’язані із двома способами вибору осі обертання тіла:

1. Нехай вісь обертання збігається з геометричною віссю циліндра, що проходить через центр інерції котка. Отже, ми будемо розглядати кочення тіла як суму двох рухів: поступального зі швидкістю центра інерції й обертального навколо осі, що проходить через центр інерції. Для поступального руху одержимо:

(1)

Так як обертаючий момент відносно осі циліндра створює лише сила тертя (момент сили інерції ми тут не розглядаємо, оскільки вісь обертання проходить через центр інерції тіла), то маємо:

Це рівняння перепишемо, з огляду на співвідношення і скорочуючиR:

(2)

Рівняння (1) і (2) містять три невідомих: Т, F, а. Відсутнє рівняння запишемо, застосувавши другий закон Ньютона для гирі, прискорення якої, дорівнює прискоренню центра котка:

(3)

Вирішивши систему (1), (2), (3), знайдемо невідомі величини а, Т:

Знаючи прискорення гирі, обчислимо шукану швидкість за відомою формулою швидкості рівнозмінного руху:

.

2. За вісь обертання виберемо вісь, що проходить через точку дотику циліндра з площиною (т.О, рис. 3), тобто будемо розглядати кочення тіла як обертання навколо миттєвої осі. Обертаючим моментом відносно цієї осі є момент сили, тому одержимо

(4)

Момент інерції циліндра відносно цієї осі знайдемо за формулою і теоремою Штейнера:

(5)

Як і в першому способі, записавши другий закон Ньютона для гирі (3), з рівнянь (2) і (4) з урахуванням співвідношеня (5) знайдемо значення прискорення а та сили Т, що збігаються з отриманими раніше.

Швидкість гирі обчислимо так само, як у першому способі.

Зауваження. Обидва способи рішення задачі основані на використанні рівнянь руху твердого тіла.