Рівняння нерозривності струменя.

Рис. 4.15.

Нехай трубка потоку має і – (рис. 4.15). Тоді маса рідини проходить через переріз за 1 секунду (за )

Через :

Через :

,

де .

Демонстрація трубок і ліній струму.

Трубка струму є як би непроникною трубкою. Частина потоку рідини знаходиться всередині трубки струму. Поперечний переріз трубки настільки малий, що швидкість рідини в усіх точках перетину однакова.

Для сталого тиску:

;

Це рівняння нерозривності для реальної рідини, що стискається.

Якщо рідина не стискається, то .

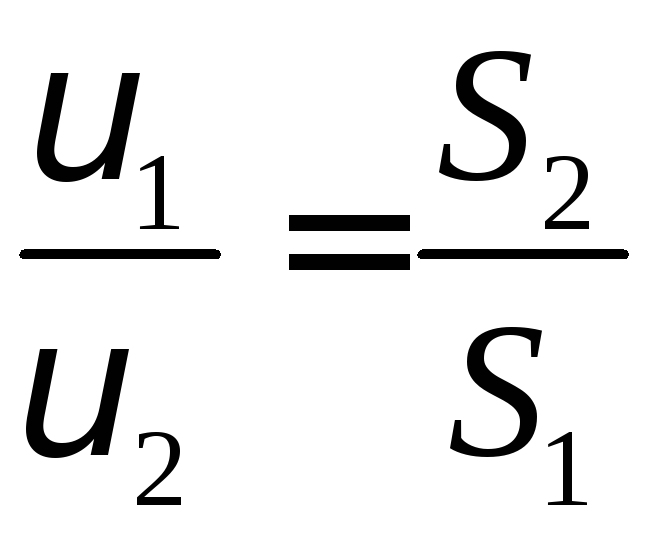; (4-21)

Таким чином, рівняння нерозривності визначає розподіл швидкостей потоку: швидкість більша в тих місцях, де трубка струму вужча, вона зменшується у напрямі розширення трубки струму (русло річки або трубки, по якій протікає рідина).

Приклад: У вузьких місцях – дуже сильний потік води (будівництво дамб).

Динаміка ідеальної рідини. Основний закон гідродинаміки (рівняння Бернуллі).

Встановимо зв’язок між тиском і швидкістю стаціонарного руху ідеальної рідини.Умовно виділимо всередині сталого потоку рідини трубку струму, в якій знаходиться об’єм рідини. Розглянемо елементарну масу рідини, обмежену перерізами і, в яких позначимовідповідно тиск, швидкість і площу перерізу (рис. 4.16).

Рис. 4.16.

Знайдемо зміну повної енергії виділеної маси за малий проміжок часу .

За цей час дана маса рідини просувається вправо, обмежена перетинами ,.

Оскільки рух рідини стаціонарний, частина рідини ,ніяких енергетичних змін не випробовує. Енергетичні зміни полягають у тому, що маса рідиниміжта, така ж як при переміщенні в положення.

Тоді повна енергія переміщеної маси рідини в І положенні:

у новому положенні:

Отже, при переміщенні з першого в друге положення повна енергія змінилася на величину:

Згідно закону збереження енергії: зміна повної енергії повинна дорівнювати роботі зовнішніх сил тиску на і .

Повна робота зовнішніх сил:

Використовуючи рівняння нерозривності струменя:

; – об’єм даної маси рідини.

Тоді:

;

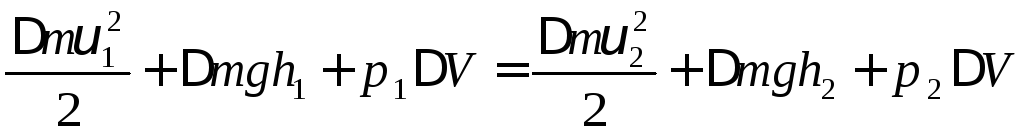
Так, як і –довільні, то отримаємо наступне рівнння

, (4-22)

яке носить назву рівняння Бернуллі.

Рівняння Бернуллі (1738 р.) (Данило Бернуллі – член Петербурзької академії наук).

Основне рівняння гідродинаміки справедливе для стаціонарного руху ідеальної рідини. Але його в наближенні можна застосувати і для реальних рідин.

Рівняння Бернуллі – наслідок закону збереження механічної енергії.

Фізичне значення вхідних в рівняння доданків.

Всі доданки мають розмірність тиску.

а) Р – називається тиск усередині руху рідини (статичний тиск) – вимірюється манометром, нерухомий відносно поточної рідини (на практиці манометром з мембраною, площина якого паралельна лініям струму);

б) доданок – гідродинамічний тиск, показує на яку величину зменшився тиск усередині рідини внаслідок її руху;

в) доданок – гідравлічний тиск, що показує на скільки зменшився статичний тиск при піднятті трубки на висоту h.

Інтерпретація рівняння Бернуллі: в сталому русі ідеальної рідини повний тиск, що складається з динамічного, гідравлічного і статичного, однаковий для всіх поперечних перерізів трубки потоку.

Постійна Бернуллі має значення тиску усередині рідини, що перебуває у стані спокою, на рівні, прийнятому за початок відліку.

Застосування рівняння Бернуллі: вимірювання повного тиску всередині рухомої рідини: трубки Піто – трубка з отвором перпендикулярним потоку (рис. 4.17в).

Трубка Прандтля – комбінація трубки Піто з манометричною трубкою, що вимірює статичний тиск. Трубкою Прандтля вимірюють динамічний тиск і використовують для визначення швидкості витікання рідини.

Манометрична трубка з перерізом паралельним лінії течії (рис. 4.17а) – для вимірювання статичного тиску.

Рис. 4.17.

Рівняння Бернуллі показує, що в поточній рідині статичний тиск зменшується із збільшенням швидкості потоку і підняттям трубки струму над нульовим рівнем.

Висновки:

1. У будь-якому місці горизонтально розташованої трубки струму повний тиск залишається величиною постійною.

2. Для S = const, V = const, тиск p+gh – називається гідростатичним тиском.