Гіроскоп, його властивості і практичне використання

Гіроскоп – це масивне симетричне тіло, що обертається з великою швидкістю навколо осі симетрії.

Гіроскоп має дві важливі властивості, завдяки яким він набув широке використання .

Перша властивість зрівноваженого гіроскопу з трьома ступенями вільності полягає в тому, що його вісь симетрії при відсутності або компенсації зовнішніх дій, намагається стійко зберігати початкове положення в просторі. Це випливає із закону збереження моменту імпульсу вільного твердого тіла. Можна наближено вважати, що повний момент імпульсу гіроскопа визначається моментом імпульсу власного обертання навколо осі симетрії.

Тоді

Тобто кутова швидкість обертання гіроскопа зберігається як за модулем так і за напрямком. Збереження напряму вектора , означає, що вісь обертання гіроскопа, по якій цей вектор направлений, зберігає своє початкове положення у просторі.

Друга властивість гіроскопа полягає в наступному: якщо до осей симетрії обертального гіроскопа прикласти силу, що намагається повернути його навколо осі, перпендикулярної до осі обертання то гіроскоп «не слухається», він починає повертатись навколо третьої осі, перпендикулярної до двох інших.

Ця властивість носить назву гіроскопічного ефекту. Його можна пояснити наступним чином: якщо на вісь обертання гіроскопа подіяти силою , яка направлена вертикально вниз, то вектор моменту цієї силибуде лежати в горизонтальній площині і прикладений в т.О опори або підвісу гіроскопа. Такий гіроскоп носить назву гіроскопа на карданному підвісі.

Момент сили намагається повернути вісь гіроскопа у вертикальній площині. Але вона, всупереч сподіванням повертається в горизонтальний площині.

Це можна пояснити, виходячи з основного закону динаміки обертального руху, записаного в формі рівняння імпульсів:

Звідси витікає, що вектор співпадає за напрямком з вектором, він перпендикулярний до осі гіроскопа і знаходиться в горизонтальній площині, тобто через елементарний проміжок часуdt вектор повного моменту імпульсу, а значить і вісь гіроскопа повернуться в горизонтальній площині на елементарний кут , таким чином, вісь гіроскопа починає обертатись навколо осі, яка паралельна діючій силі.

Процес обертання осі симетрії гіроскопа відносно осі, паралельній напрямку дії зовнішньої сили називається прецесією.

Так як гіроскоп початково встановлено горизонтально, то його вісь симетрії описує не конус, а плоску поверхню.

Рис. 4.6.

Із рис. 4.6 витікає:

Кутова швидкість прецесії прямо пропорційна величині діючого моменту зовнішніх сил і обернено пропорційна кутовій швидкості власного обертання. Навколо осі симетрії, прецесія відбувається тим повільніше, чим швидше обертається гіроскоп.

Практичне застосування гіроскопічного ефекту (на самостійне опрацювання).

Елементи статики атт. Умови рівноваги твердого тіла

а) Поняття про ступені вільності.

Ступені вільності в механіці називаються незалежні рухи, які можливі для даного тіла чи системи тіл.

Числом ступеней вільності називається число незалежних рухів, які одночасно можливі для даного тіла або системи тіл.

Матеріальна точка в результаті поступального руху в трьох незалежних напрямках має три ступені вільності.

Числом ступеней вільності називається число незалежних координат, які повністю визначають положення тіла чи системи тіл.

Вільне тверде тіло має шість ступенів вільності. Тобто для опису поступального руху тіла в просторі можна задавати координати якої-небудь точки тіла (центра мас) та кути повороту відносно трьох взаємно-перпендикулярних осей з початком у центрі мас.

б) Рівняння руху твердого тіла. Умови рівноваги.

Для опису поступального руху навколо трьох осей, що проходять через центр мас, ми можемо скласти два векторних або шість скалярних рівнянь

(4-13)

Рівняння (4.13) називають основними рівняннями динаміки руху твердого тіла.

З рівняння (4.13) випливає , що

або 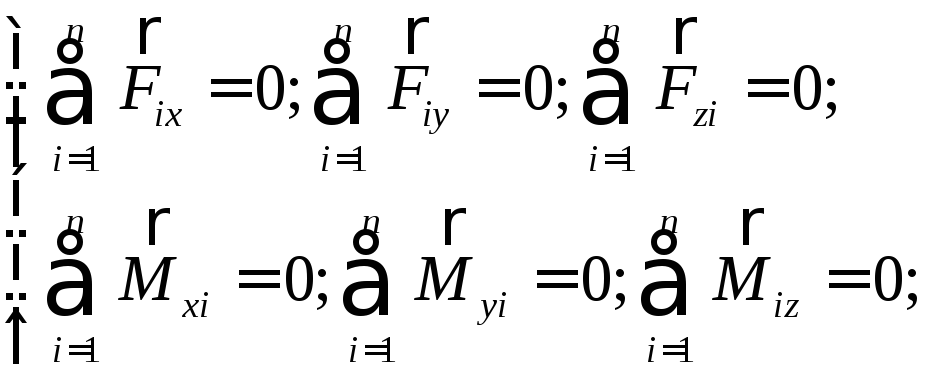(4-14)

Для того щоб тіло знаходилось у рівновазі необхідно і достатньо, щоб векторна сума усіх зовнішніх сил (головний вектор) дорівнювала нулю і щоб векторна сума моментів цих сил відносно будь якого довільного центра дорівнювала нулю.

Алгебраїчна сума проекцій зовнішніх сил на відповідні осі координат рівна нулю і алгебраїчна сума моментів цих сил відносно відповідних координат осей рівна нулю.