Визначення модуля та напряму векторів і.

Нехай матеріальна точка рухається по довільній криволінійній траєкторії відносно СВ (OXYZ) і в момент часу t займає положення А на траєкторії, маючи в цей момент швидкість . Розглянемо її положення і швидкість через довільний проміжок часуt, тобто в момент часу (t+t):

т. А: ;

т. В: (див. рис. 1.9).

Рис. 1.9.

Знайдемо зміну вектора швидкості за t. Для цього паралельно перенесемо вектор в початкову точкуА і відкладемо на ньому вектор , модуль якого. Побудуємо вектори:,,.

Тоді: з ΔDCE: .

Так, як . Звідси, враховуючи, що, маємо;.

, де

при з ΔАDC:

З другого боку: і; ;

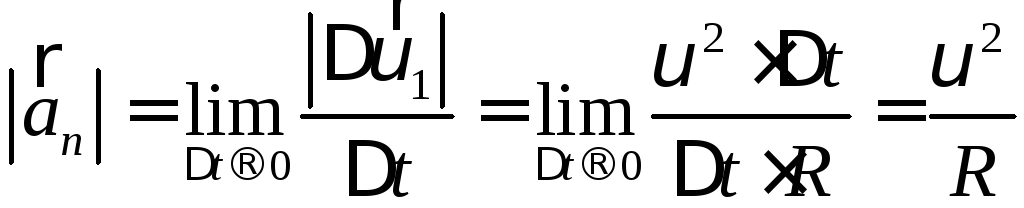
(1-14)

Модуль чисельно дорівнює квадрату лінійної швидкості, розділеному на радіус кривизни траєкторії руху.

Визначимо модуль :

, де

;

(1-15)

Модуль чисельно визначається першою похідною за часом, від числового значення вектора швидкості.

Напрям і.

При зменшені t вектор буде повертатись навколо т.А і в граничному випадку співпаде з вектором .

Вектор , що визначатиме напрямбуде зменшуватись, повертатись також навколо т.А і в граничному випадку приймає напрям, перпендикулярний .

Таким чином, ;, а значить:, тобто векторнаправлений по радіусу кривизни траєкторії до її центра.

Напрям визначається вектором.

Дійсно, при , векторприймає напрям дотичної до траєкторії в т.А. Таким чином, вектор направлений по дотичній до траєкторії в точці, яка розглядається.

Для прискореного руху: ; для сповільненого руху:.

Висновок:

(1-15а)

Рух матеріальної точки по околу (обертальний рух матеріальної точки) та його характеристики.

Найпростішим типом криволінійного руху матеріальної точки є рух точки по колу або обертальний рух. Вектор лінійної швидкості в загальному випадку змінюється як за модулем величини, так і за напрямом (рис. 1.10).

Положення довільної т. М на колі можна задати, крім дугової координати (відрізка елемента дуги, що вимірюється від початку руху) S ще й кутом повороту радіуса кола за даний проміжок часу.

Рис. 1.10.

Кут повороту радіуса кола, проведеного від центра кола в дану точку, що здійснюється за деякий проміжок часу називається кутовим зміщенням.

Основними кінематичними характеристиками обертового руху є кутова швидкість і кутове прискорення.

Кутова швидкість – фізична величина, яка характеризує бистроту зміни кутового зміщення і визначається границею відношення кутового зміщення до відповідного проміжку часу при .

(1-16)

Кутова швидкість визначається першою похідною від кутового зміщення за часом.

Кутове прискорення – фізична величина, яка характеризує бистроту зміни кутової швидкості і визначається границею відношення зміни кутової швидкості до відповідного проміжку часу при , тобто кутове прискорення визначається першою похідною за часом від кутової швидкості або другою похідною за часом від кутового зміщення.

(1-17)

Рис. 1.11.

Вектор кутового зміщення .

Нескінченно малий або елементарний поворот точки на деякий кут можна задати у вигляді направленого (вектора) відрізка, довжина якого дорівнює, а напрям співпадає з віссю, відносно якої здійснюється поворот. Для визначення напряму застосовується правило правого гвинта: напрям кутового зміщення повинно бути таким, щоб дивлячись вздовж нього, було видно поворот, який здійснювався проти ходу годинникової стрілки (рис. 1.11).