Кінематика обертального руху матеріальної точки.

37. Точка рухається по колу радіусом R = 10 см з постійним тангенціальним прискоренням . Знайти нормальне прискорення точки через час t = 20 с після початку руху, якщо відомо, що до кінця п’ятого оберту після початку руху лінійна швидкість точки = 10 см/с.

38. У першому наближенні можна вважати, що електрон у атомі водню рухається по круговій орбіті з лінійною швидкістю . Знайти кутову швидкість ω обертання електрона навколо ядра і його нормальне прискорення . Вважати радіус орбіти 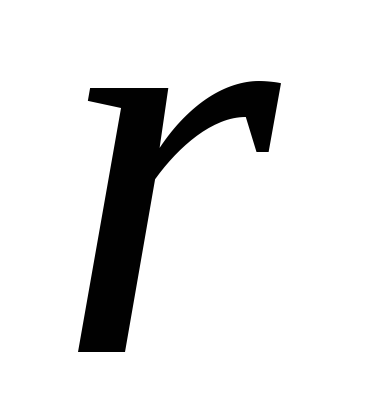=м і лінійну швидкість електрона на цій орбіті = м/с.

39. Колесо радіусом R = 10 см обертається з кутовим прискоренням ε = 3,14 рад/. Знайти для точок на ободі колеса до кінця першої секунди після початку руху: а) кутову швидкістьω; б) лінійну швидкість ; в) тангенціальне прискорення ; г) нормальне прискорення ;д) повне прискорення ; е) кут , що утворюється вектором повного прискорення з радіусом колеса.

40. Точка рухається по колу радіусом R = 2 см. Залежність шляху від часу дається рівнянням s = C, де С = 0,1 см/. Знайти нормальне і тангенціальне прискорення точки в момент, коли лінійна швидкість точки = 0,3 м/с.

41. Точка рухається по колу так, що залежність шляху від часу задається рівнянням s = A–Bt+C, де В = 2 м/с і С = 1 м/. Знайти лінійну швидкість точки, її тангенціальне , нормальне і повне а прискорення через час t = 3 c після початку руху, якщо відомо, що при t' = 2 c нормальне прискорення точки = 0,5 м/.

42. Знайти кутове прискорення ε колеса, якщо відомо, що через час t = 2 c після початку руху вектор повного прискорення точки, що лежать на ободі, складає кут = 60° з вектором її лінійної швидкості.

43. Колесо обертається з кутовим прискоренням ε = 2 рад/. Через часt = 0,5 c після початку руху повне прискорення колеса a = 13,6 см/. Знайти радіусR колеса.

44. Колесо радіусом R = 0,1 м обертається так, що залежність кута повороту радіуса колеса від часу задається рівнянням =A+Bt+C, де В = 2 рад/с і С = 1 рад/. Для точок, що лежать на ободі колеса, знайти через часt = 2 c після початку руху: а) кутову швидкість ω; б) лінійну швидкість 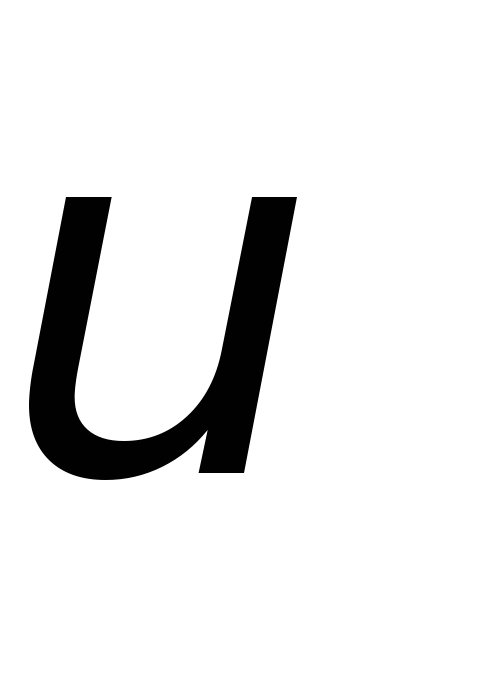; в) кутове прискорення ε; д) тангенціальне і нормальнеприскорення.

45. Колесо радіусом R = 5 см обертається так, що залежність кута повороту радіусу колеса від часу задається рівнянням =A+В+C+D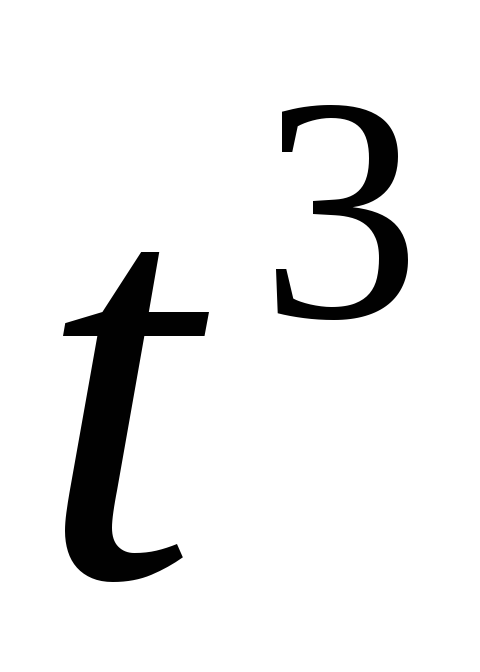, де D = 1 рад/. Для точок, що лежать на ободі колеса, знайти зміну тангенціального прискорення за одиницю часу.

46. Колесо радіусом R = 10 см обертається так, що залежність лінійної швидкості точок, що лежать на ободі колеса, від часу задається рівнянням = А–B, де А = 3 см/с і В = 1 см/. Знайти кут, що утворюється між вектором повного прискорення та радіусом колеса в моменти часуt, рівні: 0, 1, 2, 3, 4 і 5 с після початку руху.

47. Колесо обертається так, що залежність кута повороту радіуса колеса від часу задається рівнянням =А+В+С+D, де B = 1 рад/c, С = 1 рад/іD = 1 рад/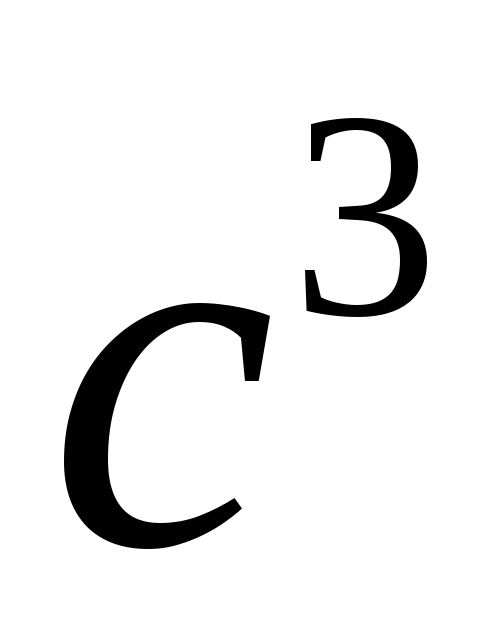. Знайти радіусR колеса, якщо відомо, що до кінця другої секунди руху для точок, що лежать на ободі колеса, нормальне прискорення становить = 3,46·10² м/.

48. У скільки разів нормальне прискорення точки, яка лежить на ободі колеса, що обертається, більше її тангенціального прискореннядля того моменту, коли вектор повного прискорення точки складає кут= 30° з вектором її лінійної швидкості?