Практичне заняття 1.3 Тема: Кінематика обертального руху матеріальної точки. Основні формули

До кінематичних параметрів обертального руху матеріальної точки (тіла) відносять кутові величини:

1. Кутова швидкість: ;

2. Кутове прискорення: ;

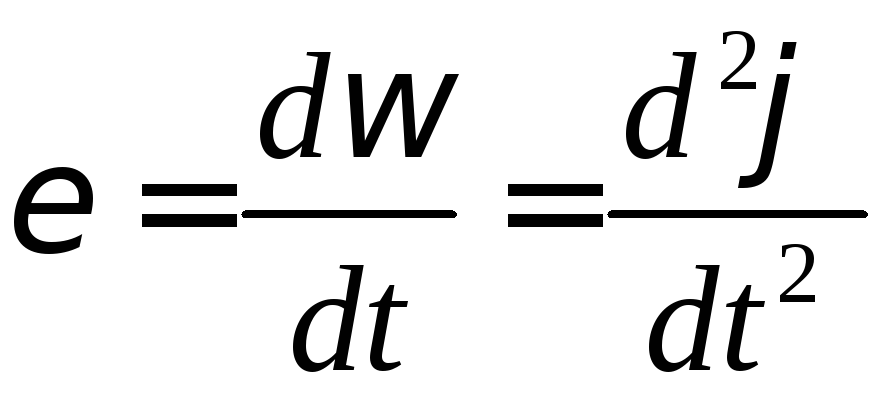Та лінійні величини:

3. Лінійна швидкість: ;

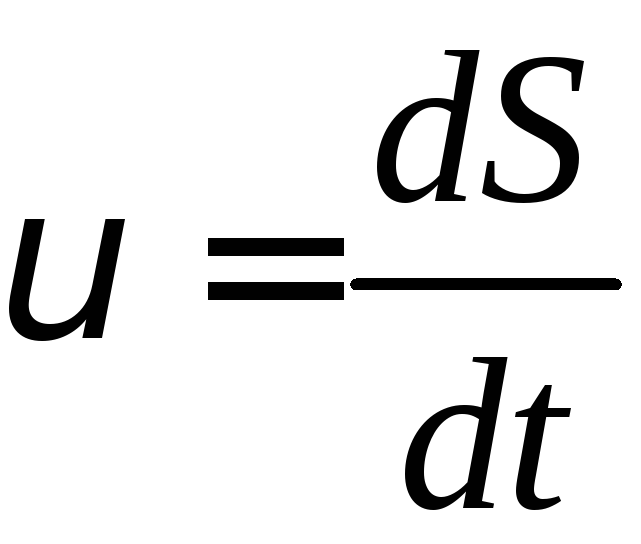4. Лінійне прискорення, яке має дві складові: нормальне і тангенціальне прискорення:

, ,

де

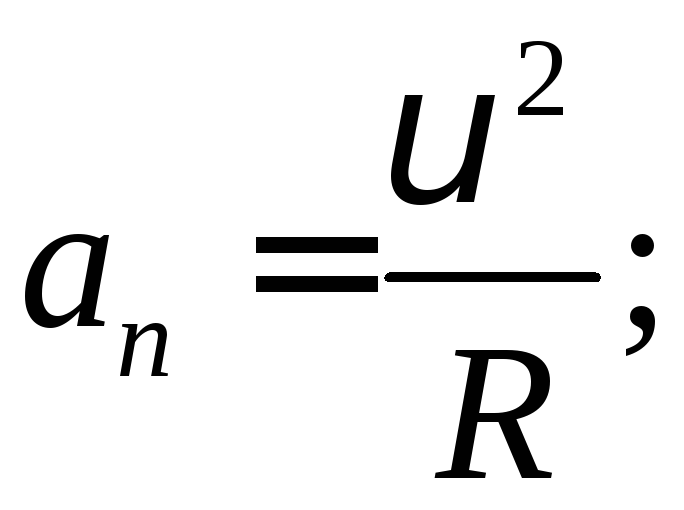
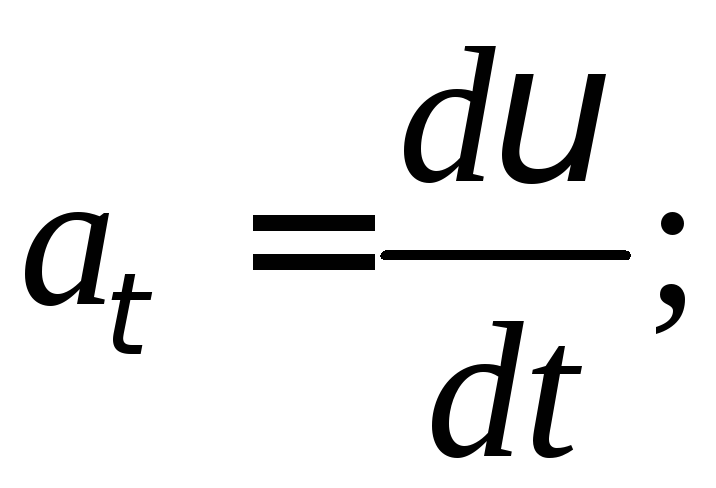
Зв’язок між лінійними і кутовими характеристиками встановлюють співвідношення:

, ,

Кінематичні рівняння рівномірного обертального руху мають вигляд:

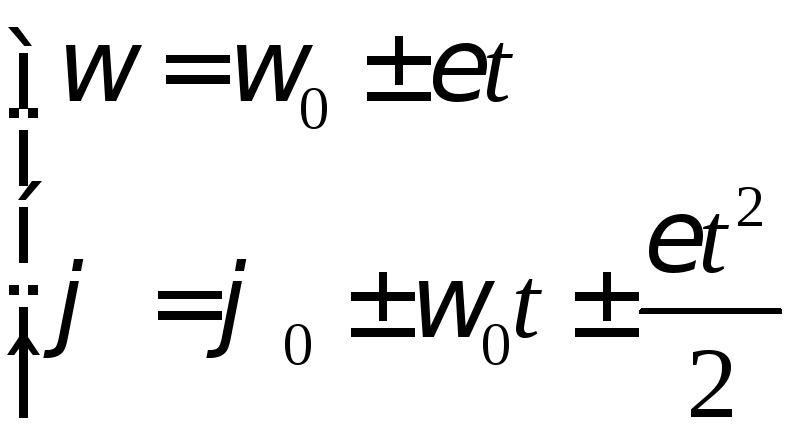Аналогія:

Допоміжні формули:

Приклади розв’язання задач

Приклад 1. Маховик, що обертався з постійною кутовою швидкістю , при гальмуванні почав обертатися рівносповільнено. Коли гальмування припинилося, маховик знову почав рухатись рівномірно, але з кутовою швидкістю. Знайти кутове прискорення маховика і тривалість гальмування, якщо впродовж рівносповільненого руху маховик зробивN = 50 обертів.

Розв’язання.

Використаємо кінематичні рівняння рівносповільненого обертального руху:

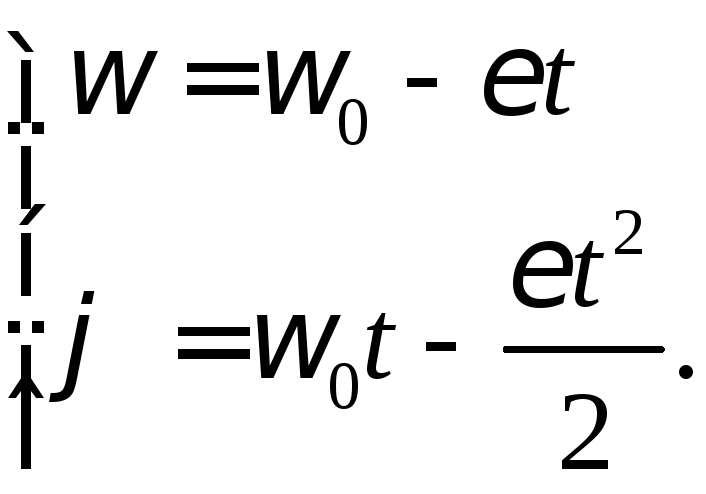
Оскільки , то розв’язок задачі зводиться до розв’язування системи рівнянь з 2-ма невідомими і t :

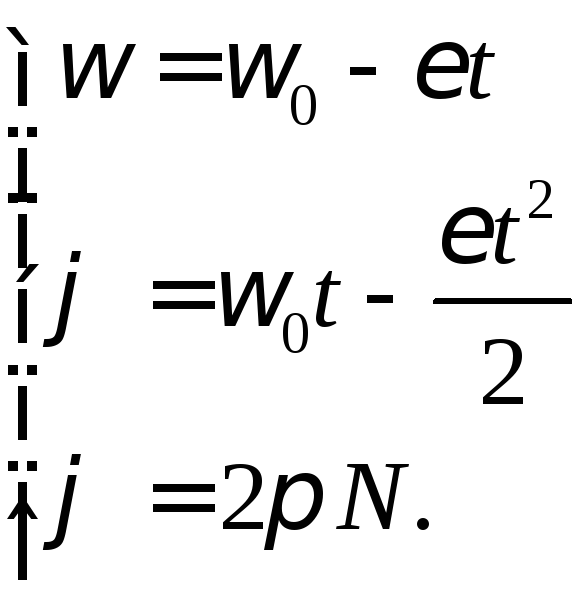
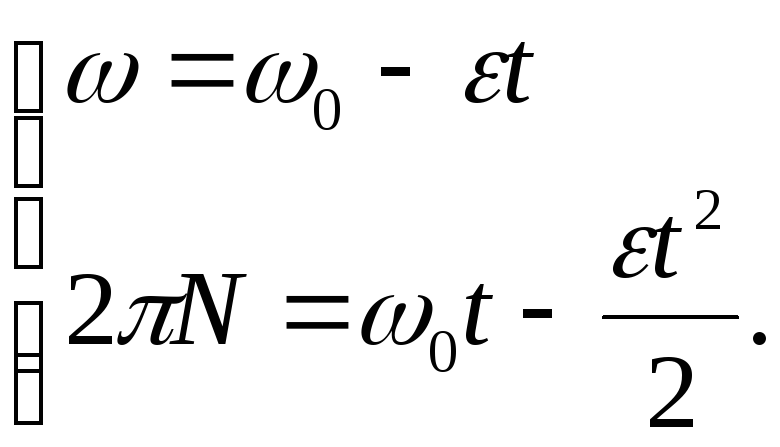
Звідси отримуємо:

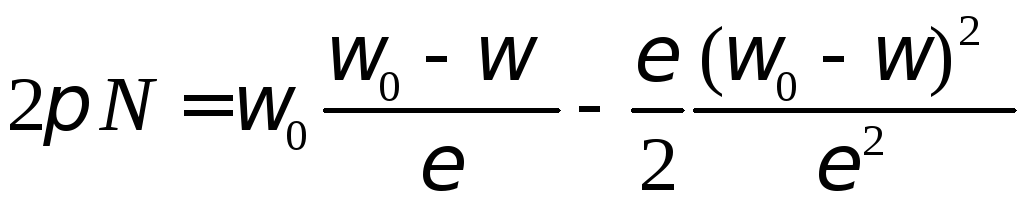
Розв’язавши рівняння отримаємо:

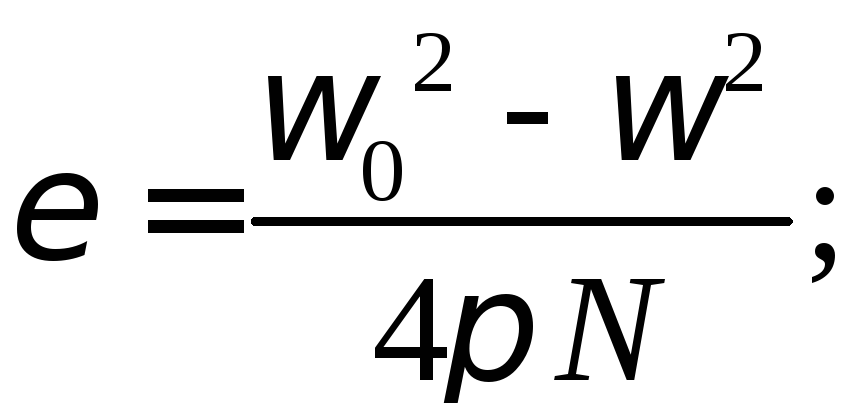
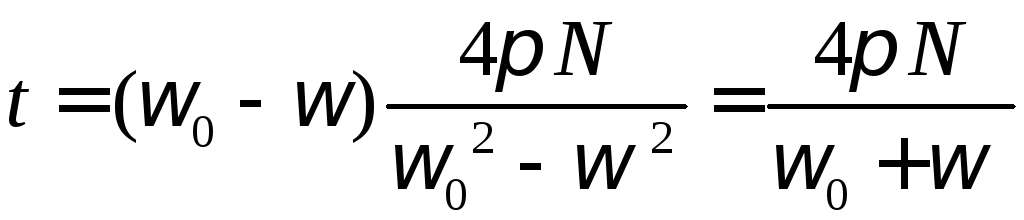
Провівши обчислення маємо:

.

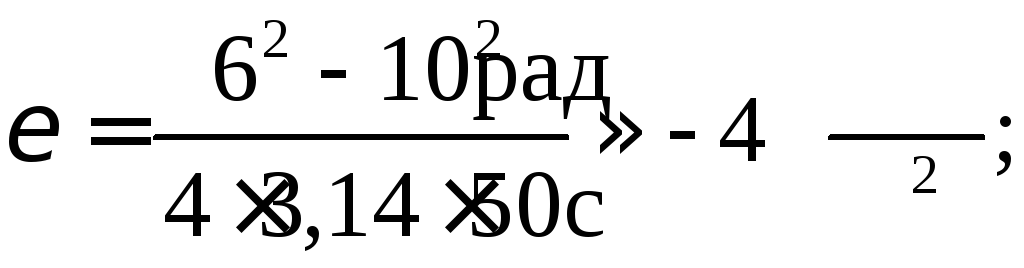
Приклад 2. Точки рухаються по колу радіусом R = 10 см з постійним тангенціальним прискоренням . Знайти тангенціальне прискоренняточки, якщо відомо, що до кінця п’ятого оберту після початку руху, швидкість точки стала рівною= 79,2 см/с.

Розв’язання.

Тангенціальне прискорення точки зв’язане з її кутовим прискоренням, таким чином:

Оскільки радіус кола відомий, задача зводиться до визначення кутового прискорення . Так як тангенціальне прискорення постійне, то і рух є рівноприскореним (без початкової кутової швидкості) = 0.

Для випадку рівноприскореного обертального руху справедливі наступні формули:

, .

Якщо радіус-вектор лежить в площинні обертання, то , деR – радіус обертання точки.

Так як

Звідси:

а .

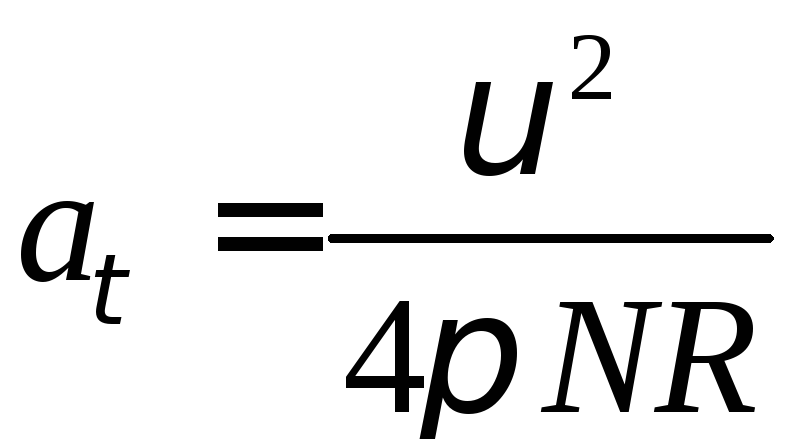Обчислення робимо, переводячи всі одиниці в СІ:

.

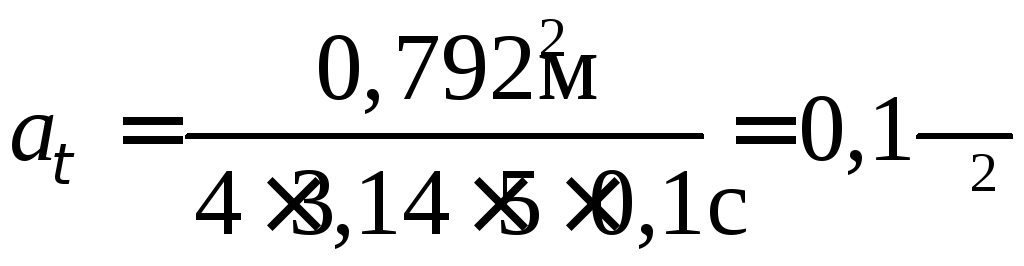Приклад 3. Колесо обертається так, що залежність кута повороту радіуса колеса від часу виражається рівнянням

, де В = 1 рад/с, С = 1 рад/с², D = 1 рад/с³. Знайти радіус колеса, якщо відомо, що до кінця другої секунди руху нормальне прискорення точок, які лежать на ободі колеса, дорівнює м/с².

Розв’язання.

Відомо, що , звідки.

Отже, задача зводиться до визначення кутової швидкості обертання. З означення кутової швидкості:

, а ,

Обчислення робимо, переводячи всі одиниці в СІ

R = м.

Приклад 4. Вал радіусом R може обертатися навколо горизонтальної осі. На вал намотана нерозтяжна нитка, на кінці якої висить вантаж P. У початковий момент часу вантаж і вал нерухомі. В деякий момент часу вантаж починає опускатися з постійним прискоренням і приводить до обертання вала. Знайти повне прискорення точок обода колеса як функцію від висотиh, на яку опускається вантаж.

Розв’язання.

Рис. 1.

Повне прискорення .

Прискорення, з яким рухається вантаж, дорівнює прискоренню кожної точки нитки і, відповідно, дотичному прискоренню точок, які лежать на ободі вала. Швидкість вантажа . Цю швидкість має будь-яка точка нитки й будь-яка точка, що лежить на ободі вала. Кутова швидкість вала:

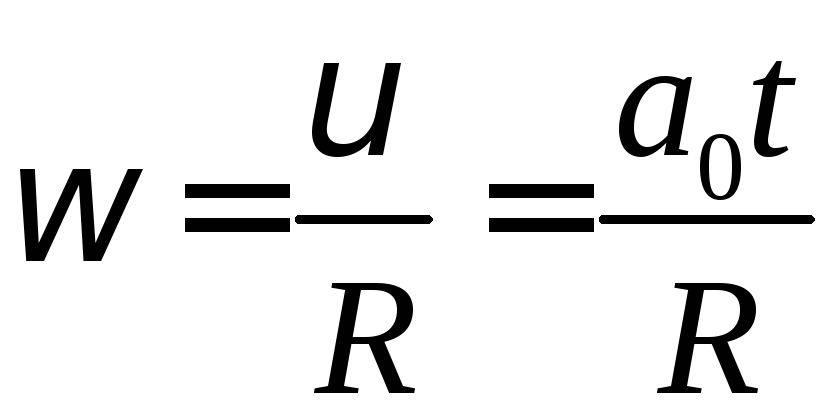
Нормальне прискорення точки, що лежить на ободі вала

Ми знайшли повне лінійне прискорення точок обода вала як функцію часу t. Час t і висота падіння вантажу зв’язані відношенням

.

Відповідно

і .