Файловый архив студентов. Файловый архив студентов.
1305 вузов, 5165 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Национальный исследовательский университет «МИЭТ»
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

material1 / different / Chung-Yu Wu - Analog Circuit Design

.pdf
Скачиваний:
51
Добавлен:
05.06.2015
Размер:
29.49 Mб
Скачать
☆

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

15-8

 

 

 

 

 

 

 

 

 

 

 

 

 

 

CHUNG-YU WU

(h) Lowpass or highpass filter, adjustable zero and pole, fixed ratio or

 

independent adjustment

 

 

 

|H|

 

 

 

 

 

 

 

 

 

C2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

gm1/(gm1+gm2)

 

 

 

 

 

 

 

 

 

Vi

 

 

 

 

 

 

 

 

 

 

 

 

gm↑

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Vo

 

 

 

 

 

 

 

 

 

gm1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

C1

C2/(C1+C2)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

g

m2

 

 

 

 

g

/(g

m1

+g

) > C

2

/(C +C )

ω

 

 

 

 

 

 

m1

 

m2

 

1

 

2

 

 

 

 

 

 

 

 

 

|H|

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

C2/(C1+C2)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

g

m

↑

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

H(s)=Vo =

gm1 + sC2

 

 

gm1/(gm1+gm2)

 

 

 

 

 

 

 

 

 

+ g

 

gm1/(gm1+gm2) < C2/(C1+C2)

 

V

s(C +C

2

)

+ g

m1

m2

ω

i

1

 

 

 

 

 

 

 

 

 

 

 

 

 

(i) Phase shifter, adjustable with gm

 

 

 

 

 

 

Vo

sC − gm1

 

C

 

H(s)= Vi

= sC + gm1 gm2 R

Vi

 

H

gm2R=1

 

Vo

180o

 

 

gm1

 

 

 

 

gm2

90o

 

gm↑

 

 

 

 

R

0o

 

ω

 

 

gm1/C

§15-2.4 Second-order Gm-Cor OTA-C filters

(a)

 

V01=

S 2C C V + SC g V + g g V

 

1 2 C

 

1 m2 B

m1 m2 A

 

 

 

 

 

S 2C C

2

+ SC g

m2

+ g

m1

g

m

2

 

 

1

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

15-9 CHUNG-YU WU

Transfer functions for the biquadratic structure (a)

Circuit Type

Input Conditions

 

 

Transfer Function

 

 

 

 

If gm1=gm2=gm

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ωo

Q (fixed)

ωo Adjustable

 

Vi=VA

 

 

 

gm1 gm2

 

 

 

 

 

 

 

 

gm

C2

Lowpass

V

and V Grounded

 

 

s2C C

+ SC g

m

2

+ g

m1

g

m2

 

 

C C

C1

 

B

C

 

1 2

 

 

1

 

 

 

 

 

1 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ωo Adjustable

 

Vi=VB

 

 

 

sc1 gm2

 

 

 

 

 

 

 

 

gm

C2

Bandpass

VA and VC Grounded

 

s2C1C2

+ SC1 gm2

+ gm1 gm2

 

 

C1C2

C1

ωo Adjustable

 

Vi=VC

 

 

 

s2C C

2

 

 

 

 

 

 

 

 

gm

C2

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

C C

Highpass

V

and V Grounded

 

s2C C

+ SC g

m2

+ g

m1

g

m2

 

 

C1

 

A

B

 

1 2

 

 

1

 

 

 

 

 

1 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ωo Adjustable

 

Vi=VA=VC

 

 

s2C C

2

+ g

m1

g

m2

 

 

 

 

gm

C2

 

 

 

 

1

 

 

 

 

 

 

 

 

C C

Notch

 

V Grounded

 

 

s2C C

+ SC g

m

2

+ g

m1

g

m2

 

 

C1

 

 

B

 

1 2

 

 

1

 

 

 

 

 

1 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(b)

ωo=

gm1 gm2

, Q =

g

1

R

C2 gm1

 

C C

2

 

m3

C g

m2

 

1

 

 

 

1

*Can implement lowpass, bandpass, highpass, and notch.

*If gm3 is fixed and gm1=gm2=gm is adjusted, the poles can be moved in a constant-Q manner.

*If gm3 is adjusted with gm1 and gm2 fixed, the pole movement in a constant-ω0 manner.

(c)

Vo3=

S 2C C V + SC g V + g g V

1 2

c

 

 

1 m2 B m2 m1 A

 

 

 

 

S 2C C

2

+ Sg

 

C + g

m1

g

m2

 

 

 

1

 

 

m3 1

 

 

 

ωo=

gm1 gm2

, Q=(

C2

)

gm1 gm2

 

 

 

C C

2

 

 

 

C

 

g

m3

 

 

 

1

 

 

 

 

1

 

 

 

 

15-10 CHUNG-YU WU

*ωo can be adjusted linearly with gm1=gm2=gm and gm3 constant => constant-bandwidth movement.

*If gm1, gm2, and gm3 are adjusted simultaneously, constant-Q pole movement.

*Interchanging "+" and "-" terminals of gm1 and gm2 and setting VA=VB=VC=Vi,

and making gm1=gm2=gm3=gm

(d)

 

gm 1

VA

gm 2

 

C1

C2

VC VB

=> 2nd-order gm adjustable phase equalizer.

V04=

V C C

S 2

+V

g

m3

sC + g

m1

g

V

c 1 2

 

 

 

B

 

 

 

 

1

 

 

 

m2 A

 

S 2C C

2

+ SC g

m3

+ g

m1

g

m2

 

 

 

 

 

 

 

1

 

 

 

1

 

 

 

 

 

 

gm 3 Vo4

ωo=

gm1 gm2

, Q=

 

1

gm1 gm2C2

 

 

 

C C

2

 

 

 

 

g

m3

 

 

C

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

1

 

 

* The adjustment of the bandpass version with gm1=gm2=gm will result in a constant bandwidth, constant gain response.

(e) Elliptic biquadratic filter

 

x x'

 

gm1

 

 

 

 

 

gm2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

VA

 

 

 

 

 

 

 

 

 

 

 

 

 

Vo

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

C1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

C2

 

 

 

 

C3

 

 

 

 

 

 

 

 

 

 

 

 

V

 

 

C

2

 

 

 

 

 

 

 

 

S 2

+ g

m1

/C C

2

 

 

 

 

 

 

H(s)=

o

=(

 

 

 

 

)(

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

)

 

C

 

+C

 

S 2

+ Sg

 

 

/(C

 

+C

) + g

 

g

 

 

/C

(C

 

+C

)

 

V

2

3

 

m2

2

m1

m2

2

 

 

i

 

 

 

 

 

 

 

 

3

 

 

 

 

1

 

3

 

 

* Can be applied to the realization of high-order voltage-controlled elliptic filters.

=>Cascading these second-order blocks with interstage unity-gain buffers. All gm's are made equal and adjusted simultaneously.

* The voltage-controlled amplifier of Fig. (g) on p.15-3 can be

inserted between x and x'. The transconductance gain of the two OTAs in the

15-11 CHUNG-YU WU

amplifier can be used as the control variable to adjust the ratio of the zero location to pole location.

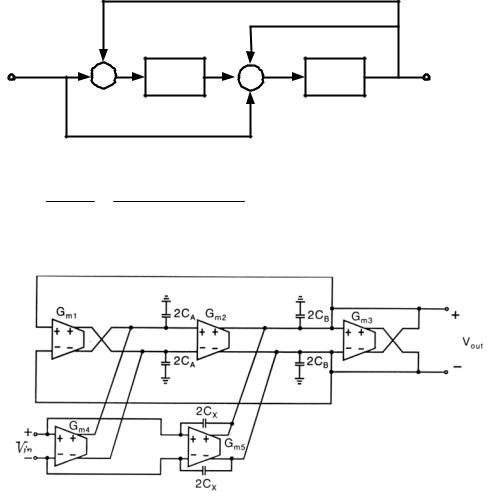
(g) General biquadratic structure

Vo=

S 2C C V + SC g V + g g V

1 2

c

 

1 m4

B

m2 m5 A

 

 

 

S 2C C

2

+ SC g

m3

+ g

m2

g

m1

 

1

 

1

 

 

* when Vi=VA=VB=VC, the ωo and Q for the poles and zeros can be adjusted by gm's to any desired value.

§15-2.5 Fully Differential Gm-C or OTA-C Filters

1. General first-order filter

H(s)=

Vout

=

K1S + Ko

 

 

 

 

 

 

 

 

 

 

 

 

 

S +ω

 

 

 

 

 

 

 

 

 

 

 

 

V

 

 

 

o

 

 

 

 

 

 

 

 

 

 

 

 

in

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

SCx +Gm1

 

 

 

S(

Cx

) +

Gm1

 

 

H(s)=

 

 

 

 

 

 

=

CA +Cx

CA +Cx

 

 

 

 

 

 

 

 

S(CA +CX ) +Gm2

 

S +

 

Gm2

 

 

 

 

 

 

 

 

 

 

 

 

 

CA +CX

 

 

=>Cx=(

 

 

K1

 

)CA , Gm1=Ko(CA+CX), Gm2=ω0(CA+CX)

1

 

 

 

 

 

− K1

 

 

 

 

 

 

 

 

 

 

 

2. General biquadratic filter

 

 

 

 

 

 

 

 

 

-ω0

 

 

 

 

 

 

 

 

 

 

 

-ω0/Q

Vin(S)

K0/ω0 +

 

 

 

1/S

ω0

+

1/S

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

K1+K2S

 

 

 

H(s)=

V (s)

=

K

S 2 + K

S + K

 

 

out

 

2

 

ωo

1

 

o

 

 

V (s)

 

S

2

+ (

)S +ωo

2

 

 

in

 

 

Q

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

15-12 CHUNG-YU WU

Vout(S)

 

V

(s)

 

S 2 (

GX

 

 

) + S(

 

 

Gms

 

 

 

 

) +

 

Gm 2Gm4

 

H(s)=

=

C +C

 

C +C

 

 

C (C +C )

 

 

 

 

 

 

 

 

 

V

(s)

 

2

 

 

 

Gm3

X

 

 

B

 

Gm1Gm2

 

 

out

 

 

 

X

 

B

 

 

 

 

 

 

A

X B

 

 

in

 

 

 

S + S(CX +CB ) + CA (CX +CB )

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Design equations:

 

CX=CB(

 

 

K2

)

 

 

where 0 ≤ K2 <1

 

 

1− K2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Gm1=ωoCA

Gm2=ωo(CB+CX)

Gm3= ωo (CB +CX )

Q

Gm4=(KoCA)/ωo

Gm5=K1(CB+CX)

15-13 CHUNG-YU WU

§15-3 CMOS Transconductor or OTA

1. CMOS transconductor using triode transistor

*Q9: operated in the triode region.

*Gm can be adjusted by Vgs9 and scaled by the current mirrors Q3/Q7 and Q4/Q8.

*Q5/Q6 are feedback devices to set the drain voltages

of Q1/Q2.

2. CMOS transconductor using varying bias-triode transistors.

* Q3 and Q4 are in the triode region.

* Gm=

 

 

1

 

 

where rds3=rds4=

 

 

 

 

1

 

 

 

 

 

 

 

r

+ r

+(r

|| r

)

 

2K

3

(V

 

−V

)

 

 

 

 

 

s1

s2

ds3

ds4

 

 

 

 

 

 

 

GS1

tn

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

1

 

 

 

I1

 

 

 

 

 

 

rs1=rs2=

 

 

 

=

 

 

 

 

VGS1-Vtn=

K

 

 

 

 

 

 

 

g

m1

 

2K

(V

−V )

1

 

 

 

 

 

 

 

 

 

 

1

 

GS1

 

tn

 

15-14 CHUNG-YU WU

3. CMOS differential-pair transconductor with floating voltage supply. Conceptual circuit:

Real circuit:

(iD1-iD2)= 4 Keq IB (V1 −V2 )

Gm=4 Keq I B

* 30~50 dB linearity.

4. CMOS bias-offset cross-coupled transconductor.

(i1-i2)=2KVB(V1-V2) Gm=2KVB

*30~50dB linearity

15-15 CHUNG-YU WU

§15-4 Design Example of Gm-C or OTA-C Filters

Ref.: 1. IEEE Trans. Circuits and Systems, pp. 1132-1138, Nov. 1986

2.IEEE JSSC, pp.987-996, Aug. 1988

1.CMOS linear transconductance amplifier (CMOS inverter-based complementary differential-pair transconductor)

VDD

VG1

M1

 

M2

Vin

Vout

 

M3

VG4

M4

 

VSS

2. Gm-C biquad (general)

VL

L

1

 

 

VB

C

C2

VH

 

1

 

 

V3

gm=2keff (VG1+ VG4 −ΣVT)

ΣVT=VTn1+VTn3+ VTP2 + VTP4

keff =

kn k p

( kn + k p )2

kn,p= 12 (ueff cox ×WL )n, p

Tunable gm amplifier symbol:

5

3

4

2

 

 

V2

Q

6

6

Vo

−C g 2 SN +C g S 2 N + g 2 N + (C C g S 2 + g g )N

H(s)= 1 m BP 1 m HP m LP 1 2 m 3 m L m BR

C1C2 gm S 2+C1 gm (gmQ − gm )S + gm

NBP: VB ≠ 0 , VL=VH=0

NHP: VH ≠ 0 , VL=VB=0

NLP: VL ≠ 0 , VH=VB=0

NBR: VL=VH=VBR, VB=0

15-16 CHUNG-YU WU

Experimental results on BP filter:

Center frequency 4MHz

TABLE I

EXPERIMENTAL FILTER DATA

Control

Automatic

 

Manual

Passband ripple

1 dB

 

0.5 dB

Stopband attenuation

 

>60 dB

Bandwidth

800 KHz

S/N in passband

≈40dB

 

75dB

Distortion (for 0.5Vpp)

 

0.5%

Max. signal level

 

1.2 Vpp

Frequency control range

1 MHz

 

1.5 MHz

 

 

 

 

Q-control range

40%

 

unlimited

Offset (reference inverter)

1mV @ Gain ≈ 50

 

 

 

 

§15-5 MOSFET-C Filters

*MOSFET-C filters are slower than Gm-C filters

Miller integration.

*Smaller speed

The load of op amps is resistive * Straightforward design methodology

15-17 CHUNG-YU WU

1. Two-transistor integrators.

(a) Active-RC integrator

 

 

 

(b) Two-transistor MOSFET-C integrator

R1 ≡ Rp1 = Rn1

R2 ≡ Rp2 = Rn2

 

 

 

 

Vdiff ≡Vpo-Vno=

ino −ipo

=

(ip1 +ip2 ) −(in1 +in2 )

 

 

 

 

 

 

 

 

SC

 

 

SC

 

 

 

 

 

1

 

 

 

1

 

 

 

 

 

=

1

 

(Vp1 −Vn1 ) +

1

 

(Vp2 −Vn2 )

 

SR C

SR

C

 

 

 

 

 

 

 

 

1

1

 

2

1

 

2.General biquadratic MOSFET-C filter Active-RC circuit:

MOSFET-C biquadratic filter:

Соседние файлы в папке different
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности