
14-20 CHUNG-YU WU
§14-7 The Design of SC Biquads (Second-Order Filter)
H(S)= |
− (K |
2 |
S 2 |
+ |
K |
S |
+ |
K |
) |
= |
V |
(s) |
||
|
|
|
ωo |
1 |
|
|
o |
|
|
out |
|
|||
S |
2 |
|
+ |
|
|
|
2 |
|
|
V (s) |
||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
Q |
S + ω0 |
|
|
|
in |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
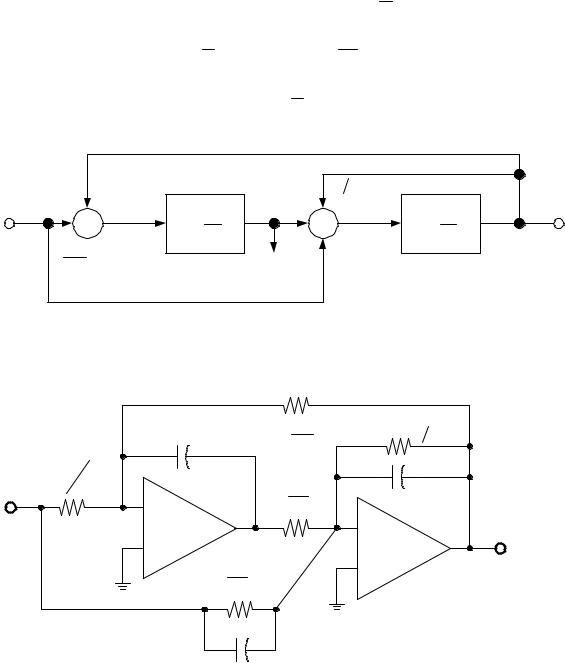
§14-7.1 Low-Q SC Biquads
Step 1: Flow diagram generation.
|
|
S2V |
=-[K |
S2+K S+K ] V (ω |
S |
+ ω2 )•V |
out |
|||||
|
|
out |
|
2 |
|
1 |
o |
in |
o Q |
0 |
||
|
|
>Vout=- |
1 |
[(K1+K2S)Vin+( Wo ) •Vout+ ωo •V1) |
||||||||
|
|
|
|
S |
|
|
|
|
Q |
|
|
|
|
|
|
|
where V1= |
1 |
[(Ko/ωo) |
•Vin+ωo •Vout] |
|||||
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
−ω0 |
|
|
|
|
|
|
Vin |
|
|
|
1 |
ω0 |
ω0 |
Q |
|
− 1 |
|
||
|
|
− |
|
|
|
Vout |
||||||
− |
K0 |
|
S |
V |
|
|
|
|
S |
|
||
|
ω |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
K1 + K2 S |
|
|
|
|
|
|
|
|||
Step2: Active-RC design
|
|
|
CA =1 |
− |
1 |
|
Q ω0 |
|
ω0 |
|
|
|
ω0 |
|
|
− |
K0 |
|
|
1 |
|
CB =1 |
|
Vin |
|
− |
|
|
|||
|
|
|
ω0 |
− |
Vout |
||
|
|
|
+ |
|
|
||
|
|
|
|
|
|
||
|
|
|
1 |
|
|
+ |
|
|
|
|
K1 |
|
|
|
|
K2

|
|
|
|
|
|
14-21 |
|
Step 3: SCF |
|
|
|
|
CHUNG-YU WU |
||
|
|
|
|
|
|||
|
|
|
C2 |
|
|
|
|
|
|
C =1 |
|
|
|
φ1 |
|
|
|
A |
|
C4 |
CB=1 |
φ2 |
|
|
|
|
|
|
|||
φ2 |
C1 |
|
|
|
|
||
- |
|
C3 |
|
|
|||
Vin |
|
|
- |
|
|||
|
OP1 |
φ2 |
φ2 |
|
|||
φ1 |
φ2 |
+ |
OP2 |
Vout |
|||
φ1 |
|
||||||
|
|
|
φ1 |
+ |
φ2 |
||
|
|
C1' |
|
|
|
||
|
|
|
|
|
|
||
C1"
C1 = T * Ko/ωo= |
|
A |
|
* ωo * T= |
|
A |
|
1 |
|
A |
|
|
Ko |
|||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
dc |
|
|
|
dc |
|
|
x |
|
dc |
|
|
ωo |
2 |
|
C2 |
= C3=ωo * T= |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
C4 = (ωo * T/Q)= |
|
1 |
> |
Q |
|
= |
CA |
(not suitable for high Q) |
|||||||
|
Qx |
ωoT |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
C4 |
|||||
C1'= K1 |
* T =K1 |
|
1 |
|
|
|
|
|
|
|
|
|
|||
ωo x |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
C1" = K2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CA/C2= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωoT |
|
> |
fo= |
fs |
|
fo: center (cutoff) frequency |
|||||||||
|
|
|
|||||||||||||
X= |
|
1 |
|
|
2πx |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ωoT |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Step 4: refinement
Z-domain block diagram (If the accuracy is not good, change to Z-domain diagram)
-C2Z-1
|
|
|
C4 |
|
-C1Z-1 |
-1/CA |
C3 |
-1/CB |
Vout |
Vin |
1-Z-1 |
|
1-Z-1 |
|
|
|
|
||
|
C '+C "(1-Z-1) |
|
|
|
|
1 |
1 |
|
|

14-22 CHUNG-YU WU
C1" = a0 C1' = a2-a0
C1 = 1/C3 * (a0+ a1+ a2)= 1 (2C1"+C1'±a1)
C3
C4 = b2 -1
C2 * C3 = b1 + b2 + 1 C2=C3
In this diagram, each op-amp and its feedback capacitor (CA or CB) is replaced by its voltage-to-charge transfer function.
|
Qout (z) |
|
= |
−1/ Cf |
= |
Vout (z) C |
|
|
|
|
|
|
|
|
||||||||
|
Vin (z) |
|
1− z −1 |
|
|
|
Vin |
(z) |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Here Cf is the feedback capacitor. |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
Similarly, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
C * (1-z-1) |
for an unswitched capacitor (e.g. C1") |
|||||||||||||||||||
|
|
C |
|
|
for a non-inverting capacitor (C1', C3, C4) |
|||||||||||||||||
|
-C * z-1 |
|
|
for an inverting capacitor (C1, C2) |
|
|
||||||||||||||||
From the block diagram, the exact transfer function is |
||||||||||||||||||||||
|
V (z) |
= |
− |
(C '+C ")z2 |
+ (C C |
|
−C '−2C ")z + C " |
|||||||||||||||
|
|
out |
|
1 |
|
1 |
|
|
|
1 3 |
|
|
1 |
|
1 |
1 |
|
|||||
|
|
V (z) |
|
(1 + C |
4 |
)z |
2 + (C |
C |
3 |
−C |
4 |
− 2)z +1 |
|
|
||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
in |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||
As compared to H(z) specifications, the capacitances can be determined.
H(z) = - |
a |
2 |
* z2 |
+ a * z + a |
0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
b |
* z2 |
+b * z +1 |
|
|
|
|||||
|
|
|
|
|||||||
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TYPES |
|
|
|
|
|
|
COEFFICIENTS |
|||
|
|
|
|
|
|
|
|
|
|
|
L-P CASE |
|
|
|
|
|
|
C1'=C1"=0 |
|||
|
|
|
|
|
|
K1=K2=0 a0=a2=0 |
||||
|
|
|
|
|
|
|
||||
B-P CASE |
|
|
|
|
|
|
C1=C1"=0 |
|||
|
|
|
|
|
|
K0=K2=0 a0=0,a1=-a2 |
||||
|
|
|
|
|
|
|
||||
H-P CASE |
|
|
|
|
|
|
C1=C1'=0 |
|||
|
|
|
|
|
|
K0=K1=0 |
a0=a2= - |
a1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
2 |
|
|
NOTCH CASE |
|
|
|
|
C1'=0 |
|||||
|
|
|
|
K1=0 |
a2=a0 |
|||||
|
|
|
|
|
|
|
||||


14-24 CHUNG-YU WU
C1=K0 |
T/ω0 = ( |
K0 |
)ω |
T |
= |
|
A |
|
ω |
T |
|||||
|
|
||||||||||||||
|
|||||||||||||||
|
|
|
ω 2 |
|
o |
|
|
|
|
dc |
|
0 |
|
||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||
C2 |
C3 ω0T |
|
|
|
|
|
|
|
|
|
|
||||
C4 |
|
1 |
(instead of |
|
Q |
|
) |
|
|
|
|
|
|||
ω0T |
|
|
|
|
|
|
|||||||||
Q |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
C1' K1/ω0
C1" K2
4. Z-domain block diagram of a high-Q biquad:
|
|
|
|
|
|
|
C2 |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
C4 (1− Z −1 ) |
|
|
|
|
|
|
||||
C |
'' (1− Z −1 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
C + |
|
−1 CA |
|
|
−C3 Z −1 |
|
+ |
−1 CB |
|
Vout |
||||
in |
|
1− Z |
−1 |
V |
|
|
1−Z |
−1 |
|
||||||
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
C '' (1− Z −1 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
H(Z)= − |
C |
"Z 2 + (C C |
|
+ C |
'C |
|
− 2C |
")Z + (C |
"−C |
'C |
) |
|||
|
1 |
|
1 |
|
3 |
1 |
|
3 |
1 |
|
1 |
1 |
3 |
|
|
|
|
|
Z 2 + (C2C3 + C3C4 − 2)Z + (1 −C3C4 ) |
|
|
||||||||||
|
Choose C2=C3 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Coefficient matching: |
|
|
|
|
|
|
|
|
|
|
|
|||
C1"= a2 b2
C1'=(C1"- ao ) / C3 = a2 −ao b2 b2 c3
C1=(a1/b1-C1'C3+2C1")/C3=(a0+a1+a2)/(b2c3)
C4=(1- 1 ) /C3 b2
C32=C22=(b1/b2-C3C4+2)=(b1+b2+1)/b2

14-25 CHUNG-YU WU
§14-7.3 Design Examples
Example 1: Low-Q Lowpass SCF Biquad
|
|
|
|
|
|
|
C2 |
|
|
|
φ1 |
|
|
|
|
|
|
|
|
|
φ2 |
|
|
|
|
|
|
|
|
|
|
|
C4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CA |
|
|
|
|
|
CB |
|
vin |
|
|
|
− |
|
|
|
|
|
|
|
φ2 |
C1 |
φ1 |
|
φ2 |
|
C3 |
φ2 |
− |
vout |
||
|
φ1 |
φ2 |
+ |
|
|
+ |
|||||
|
|
|
|
φ1 |
|
φ1 |
|
||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
4 |
|
|
|
|
CA=CB=6.3 |
C1=4 |
H (S) = S 2 +1.2S +1 |
|
|
|||||||
C2=1 |
C3=1 |
C4=1.2 |
fc |
= |
|
fs |
|
fc: CENTER FRE. |
|
||
2 •π •CA |
fs: SAMPLING FRE. |
||||||||||
Example 2: Low-Q Bandpass SCF Biquad |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
C2 |
|
|
|
φ1 |
|
|
|
|
|
|
|
|
|
C4 |
φ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CA |
|
|
|
|
|
CB |
|
vin |
|
|
|
− |
|
|
|
|
|
|
|
φ2 |
|
φ1 |
|
φ2 |
|
|
φ2 |
− |
vout |
||
|
φ1 |
φ2 |
+ |
|
|
C3 |
+ |
||||
|
|
|
|
||||||||
|
|
|
|
φ1 |
|
φ1 |
|
||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
C ' |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
CA=CB=6.3 |
C1'=2 |
H (S) = |
|
4 |
|
|
|
|
|||
2 +1.2S +1 |
|
|
|||||||||
|
|
|
|
S |
|
|
|||||
|
|
|
|
|
|
fs |
|
fc: CENTER FRE. |
|||
C2=1 |
C3=1 |
C4=1.2 |
fc = 2 •π |
•C |
A |
fs: SAMPLING FRE. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|

14-26 CHUNG-YU WU
Example 3: High-Q Low-pass SCF Biquad
|
|
|
|
|
|
|
|
|
|
|
C2 |
|
|
|
|
φ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
φ2 |
|
|
|
|
|
|
|
|
CA |
|
|
C4 |
|
|
|
|
|
|
φ2 |
|
C |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
C |
|
|
CB |
|
||||
Vin |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
φ2 |
|
- |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|||
|
|
|
|
|
|
|
|
φ |
|
|
φ |
|
|
|
||
|
|
|
|
|
|
|
+ |
|
2 |
|
1 |
|
Vout |
|||
|
φ |
|
|
φ |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
1 |
|
|
|
|
φ2 |
|
+ |
|
|||||
|
|
|
|
|
|
|
φ |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
CA=CB=6.3 |
C1=4 |
|
|
|
|
|
H (S) = S2 + |
4 |
|
|||||||
|
|
|
|
|
S |
+1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.25 |
||
C2=1 |
C3=1 |
C4=1.2 |
|
|
|
|
|
|
fc = |
fs |
|
|||||
|
|
|
|
|
|
2 •π |
•C |
A |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fc: CENTER FRE. |
|||
Example 4: High-Q Band-pass SCF Biquad |
|
fs: SAMPLING FRE. |
||||||||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
C2 |
|
|
|
|
φ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vin |
C'1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
φ2 |
|
|
|
|
|
|
|
CA |
|
|
C4 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
φ2 |
- |
|
|
|
C3 |
|
|
CB |
|
|
||
|
|
|
|
|
|
|
|
- |
|
|
|
|||||
|
|
|
|
|
|
φ |
|
|
φ |
|
|
|
|
|||
|
|
|
|
|
|
+ |
|
2 |
|
1 |
|
|
Vout |
|||
|
|
φ |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
|
|
|
|
|
+ |
|
|
||||
|
|
|
|
|
|
|
φ1 |
|
φ2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
CA=CB=6.3 |
C '1=2 |
|
|
|
|
|
H (S) = |
|
2S |
|
||||||
|
|
|
|
|
S2 +1.2S +1 |
|||||||||||
C2=1 |
C3=1 |
C4=1.2 |
|
|
|
|
|
|
fc = |
fs |
|
|||||
|
|
|
|
|
|
2 •π |
•C |
A |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fc: CENTER FRE. fs: SAMPLING FRE.

14-27 CHUNG-YU WU
Frequency response of low-Q Low-pass SCF biquad
CENTER FREQUENCY: 1K Hz
SAMPLING FREQUENCY: 39.6 Hz
CALCULATED
○ COMPUTED BY SWITCH CAP × EXPERIMENTAL

14-28 CHUNG-YU WU
Frequency response of low-Q Band-pass SCF biquad
CALCULATED
CENTER FREQUENCY: 1K Hz
SAMPLING FREQUENCY: 39.6 Hz
○ COMPUTED BY SWITCH CAP × EXPERIMENTAL

14-29 CHUNG-YU WU
Frequency response of High-Q Low-pass SCF biquad
CALCULATD
CENTER FREQUENCY: 1K Hz
SAMPLING FREQUENCY: 39.6 Hz
○ COMPUTED BY SWITCH CAP × EXPERIMENTAL

 Q
Q